Рівне

Принцип невизначеності Ґейзенберга

Розглянемо статус таких фізичних величин як положення та імпульс мікро­частинки у квантовій механіці. Поставимо питання таким чином: чи не будуть спостережувані в дослідах властивості, наприклад, електрона заважати одно­часному вимірюванню значень координат та імпульсу електрона?

а) Вимірювання координати електрона, який має точне значення імпульсу,

Значення координати електрона вимірюється за допомогою екрана з однією щілиною. Вимірювання проводиться після „приготування” фізичного стану електрона з імпульсом, рівним 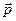. Спрощена схема експериментальної установ­ки приведена на рис. 1.

Рис. 1. Схема експериментальної установки для вимірювання дифракційної картини розсіяння електрона на щілині.

Джерело випромінює електрон з точним значенням імпульсу 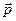, що має напрям, перпендикулярний до осі Ox. Вздовж цієї осі розміщено екран з щіли­ною шириною Δ x. Пучок електронів, які вилітають із джерела, „розріджено” настільки, що на дистанції джерело – щілина – детектор у кожний момент часу перебуває тільки один електрон. Отже, у кожному експерименті кожний наступний електрон пучка проходить крізь щілину незалежно (без можливого впливу з боку інших електронів пучка) і тільки після цього фіксується детекто­ром. У цьому й полягає суть досліду з т. з. „поодинокими” електронами.

Багатократне „поодиноке” проходження електрона через щілину свідчить, що є тільки певна імовірність потрапляння електрона в точку екрану з коорди­натою x. Тобто далеко не всі електрони потраплятимуть у точку екрану, що ле­жить строго супроти джерела і щілини. Існує відмінна від нуля імовірність потрапляння електрона в інші точки певної області екрану, як це показано на рис. 1. Вказана область зосереджена у деякому околі точки x= 0. За частотою потрапляння електронів у детектор визнають криву імовірності W (x) потрап­ляння електрона у точки з різними координатами x. Отже, фізичний стан електрона у момент його проходження крізь щілину має імовірнісну природу.

Картина, яку отримуємо на екрані детектора після багатократного повто­рення досліду, має дифракційний характер. Вона є аналогічною до картини, яку передбачає т. з. гіпотеза Луї де Бройля, тобто схожа на ту, яку б ми отримали при заміні джерела електронів джерелом хвиль довжини 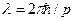і після цього повторили описаний вище дослід.

Складається враження, ніби кожний наступний електрон „знає”, у яку точку екрана з детектором потрапив попередній електрон і „вибирає” для себе таку точку x, щоб утворилася згадана вище дифракційна картина.

Проаналізуємо окремий акт проходження „поодиноких” електронів крізь щілину. Очевидно, щоб в момент такого проходження електрона, нам стає відо­ма його „іксова” складова положення – не точно, а з невизначеністю Δ x. Одно­часно можна уявити, що в цей момент із центра щілини (тобто із точки О на рис. 1) під певним кутом α видно на екрані з детектором геометричні розміри першого дифракційного максимуму. За відомими законами оптики величина кута α знаходиться зі співвідношення

Δ x∙ sin α ≥ λ, (1.3)

де згідно з гіпотезою Луї де Бройля 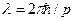, а p∙ sin α= Δ p_x ≠ 0.

Отже, проведений аналіз експерименту з вимірювання координати електро­на приводить до базового співвідношення квантової механіки, а саме, до т. з. співвідношення невизначеностей Ґейзенберга:

Δ x∙ Δ p_x ≥ h. (1.4)

б) У літературі описані й інші „уявні” експерименти з вимірювання коорди­нати та імпульсу мікрочастинки. Зокрема, дослід з вимірювання імпульсу електрона за ефектом Доплера або ж дослід з вимірювання імпульсу електрона, який вилітає через коліматор певного діаметра і далі рухається у заданому од­норідному магнітному полі. За відхиленням від початкового напряму руху цього електрона у магнітному полі судять про точне значення імпульсу елект­рона. Є й інші „мисленневі”, „уявні” та „ідеально досконалі” експерименти, і всі вони приводять до таких співвідношень:

, (1.5)

, (1.6)

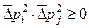, (1.7)

i, j = 1, 2, 3.

Тут використано стандартні позначення для середньоквадратичних відхилень (похибок) координат і проекцій імпульсу. Через x ₁, x ₂, x ₃ та p ₁, p ₂, p ₃ позначено, відповідно, x, y, z та p_x, p_y, p_z. Символ δ _ij – є відомий символ Кронекера. Співвідношення (1.5) – (1.7) є співвідношеннями невизначеностей Ґейзенберга для середньоквадратичних відхилень канонічно спряжених коор­динат та імпульсу (1927р.). При побудові математичного апарату квантової ме­ханіки їх слід розглядати як базовий принцип, який є узагальненням результатів експериментів з вимірювання положення та імпульсу мікрочасток. Інтерпрета­ція та методологічне тлумачення Ґейзенбергівського принципу невизначенос­тей, як і ряд інших гносеологічних проблем квантової теорії, до тепер зали­шається предметом наукових дискусій з боку фізиків та філософів.

в) Досліди показують, що електрон не можна розглядати як класичну час­тинку, яка під впливом електромагнітного поля рухається згідно законів кла­сичної механіки. Адже рух класичної частинки завжди відбувається за деякою траєкторією, а отже, в кожний момент часу у неї є точні значення координат та імпульсу. Це й дозволяло у класичному випадку корект­но задавати стан класичної мікрочастинки шістьома числами – значеннями координат векторів та . Наведені вище експерименти свідчать, що немає сенсу говорити про одночасне точне зна­чення координат та імпульсу мікрочастинки, скажем електрона. Мікрооб’єктам притаманна властивість мати одночасно значення цих величин тільки з певними відхиленнями (невизначе­ностями). Ці відхилен­ня неодмінно мають задовольняти співвідношенням Ґейзенберга.

Для встановлення величин, що описують стан мікрочастинок у квантовій механіці (тобто прийти до поняття хвильової функції) слід розглянути експери­менти з проходження електронів крізь дві щілини. Розгляд цього експерименту буде предметом нашої наступної лекції.

Отже, так ми дізнаємося, що мікрочастинки у порівнянні з класичними об’єктами проявляють нові властивості, які не є притаманними „світу класичних об’єктів”. Мікрочастинці неможливо приписати прояви як „чистої класичної корпускули”, так і „чистої реальної класичної хвилі”. Вона одночасно проявляє властивості і того, і другого. У мікросвіті, як ми далі побачимо, не витримується лапласівський детермінізм, відсутнє „стовідсоткове”, достовірне передбачення подій. Натомість приходить імовірнісний, стохастичний опис процесів, що відбуваються в мікросвіті.

Дата добавления: 2015-06-04