Необходимое число наблюдений для будущих исследований

,

где C_v – расчетный коэффициент вариации;

p – заданная точность (в курсовой работе точность принять 2 %);

К – коэффициент порогового уровня доверительной вероятности

(К₁=1,00; К₂=1,98; К₃=2,63)

Например: C_v =29,94 %; p = 2 %;К₁=1,00; К₂=1,98; К₃=2,63

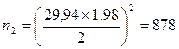шт.

шт.

шт.

В курсовой работе рассчитать необходимое число наблюдений для будущих исследований для всех трёх пороговых уровней доверительной вероятности.

Статистическое заключение

В результате анализа большой выборочной совокупности в виде измерения диаметра деревьев на высоте 1,3 м в сосновом древостое получили следующие статистические показатели с их ошибками репрезентативности:

- средняя арифметическая величина 24,88 ± 0,74 см;

- стандартное отклонение (среднее квадратичное отклонение) 7,45 ± 0,53 см;

- коэффициент вариации 29,94 ± 2,30 %, которому по шкале Мамаева соответствует повышенный уровень изменчивости;

- коэффициент дифференциации 39,46 %, которому по классификации соответствует значительная степень дифференциации.

Точность опыта 2,99± 0,23 %, по которой можно сделать вывод о том, что процент расхождения между генеральной и выборочной средней невелик. Следовательно по выборке можно сделать достоверное заключение о все совокупности в целом.

Все статистические показатели достоверны, т. к. их отношение к ошибкам репрезентативности больше 3 во всех случаях.

Доверительный интервал генеральной средней 29,34 ÷ 32,82 см. Расстояние между точками интервала невелико, следовательно выборочная совокупность достаточно точнее характеризует генеральные параметры.

Необходимое число наблюдений для будущих исследований, которое бы обеспечивало заданную точность 2% при известном коэффициенте вариации 29,94 % и трех пороговых уровнях доверительной вероятности следующее:

- для 1^го порогового уровня 224 штук;

- для 2^го порогового уровня 878 штук;

- для 3^го порогового уровня 1550 штук.

1.2.4 Расчёт показателей центральной тенденции

К показателям центральной тенденции эмпирической совокупности относятся:

- средняя величина (средняя арифметическая, средняя арифметическая взвешенная, средняя квадратическая, средняя геометрическая, средняя гармоническая)

- мода

- медиана

Мода и медиана – это структурные средние.

Средняя величина ()– это одна из основных характеристик эмпирической совокупности и отражает уровень, по отношению к которому колеблются значения вариант в ней. Способ вычисления среднего значения изучаемого признака зависит от того, что, в конечном счете, должна характеризовать эта средняя величина.

Для большой выборочной совокупности, в курсовой работе, средняя величина рассчитана, как средняя арифметическая взвешенная по формуле:

Например: x = 2488 / 100 = 24,88 см. (смотри тему: большая выборка стр. 13)

Мода ( М_о или ) – наиболее часто встречаемая варианта в эмпирической совокупности. Класс с наибольшей частотой называется модальным. Например, имеется следующий рад распределения деревьев по ступеням толщины (по диаметрам):

Класс I II III IV V VI VII VIII IX X

Групповая варианта (х_i) 8 12 16 20 24 28 32 36 40 44

Частота класса (n_i) 2 4 11 16 30 14 10 8 3 2

Наибольшее количество вариантов находится в V классе – 30 штук. Следовательно V класс – модальный. Соответственно варианта, которая наиболее часто встречается в данной выборочной совокупности, равна 24 см. Она же будет модой.

= 24 см.

Для определения моды можно использовать формулу:

, где

х_нm – нижняя граница модального класса (22 см)

С – классовый интервал (4 см)

n_m – частота модального класса, т.е класса с наибольшей частотой (30 шт)

n_m-1 – частота класса, предшествующего модальному (16 шт)

n_m+1 – частота следующего за модальным класса (14 шт)

Тогда для приведённого ряда распределения мода численно будет равна:

Медиана ( или ) – это значение признака относительно, которого ряд распределения делится на две равные по численности части. Медиана – это варианта ряда которая занимает срединное в нём положение и делящая всю совокупность на две равные половины. Для небольших выборок определяется довольно просто. Для этого варианты выборки выстраивают в порядке возрастания и если число вариантов нечётное, то центральная варианта и будет его медианой.

Например имеем ряд чисел:

Групповая варианта (х_i) 8 12 16 20 24 28 32 36 40

Тогда медиана будет равна 24 см, т.к она занимает срединное положение, по обе стороны от неё расположено по 4 варианты.

= 24 см.

При чётном числе вариантов медиана определяется по полусумме двух соседних вариант, расположенных в центре ряда.

Например по большой выборочной совокупности медиана будет равна:

Групповая варианта (х_i) 8 12 16 20 24 28 32 36 40 44

= (24+28)/2 = 26 см.

Если варианты выборочной совокупности сгруппированы в вариационный ряд, то медиану можно определить следующим образом. Сначала необходимо произвести накопление частот от класса к классу, при этом варианты ряда должны быть выстроены в порядке возрастания (т.е от меньшего к большему).

Например:

Класс I II III IV V VI VII VIII IX X

Границы классов 6 - 10 – 14 – 18 – 22 – 26 – 30 – 34 – 38 – 42 - 46

Групповая варианта (х_i) 8 12 16 20 24 28 32 36 40 44

Частота класса (n_i) 2 4 11 16 30 14 10 8 3 2

Накопленная частота (Σ n_i) 2 6 17 33 63 77 87 95 98 100

Далее медиана определяется по формуле:

, где

х_нme –значение нижней границы класса в котором находится медиана или класса в котором содержится половина накопленных частот (22 см, т.к N/2 = 100/2 = 50 шт. находится в V классе)

C – величина классового интервала (4 см)

S₁ – полусумма общей численности ряда (N/2 = 100/2 = 50 шт.)

S₂ – число накопленных частот класса, предшествующего классу с медианой (33 шт.)

n_me – частота того класса в котором находится медиана (30 шт.)

Медиана может быть определена и графическим путём по кумуляте. Для этого на оси ординат отмечают точку, соответствующую половине накопленных частот ряда распределения. Затем из этой точки восстанавливают перпендикуляр дог пресечения с кумулятой. Опущенный из точки пересечения на ось абсцисс перпендикуляр указывает значение медианы.

Например: полусумма накопленных частот рада распределения равна 50 шт. Отметив точку на оси ординат равную 50, проводим перпендикуляр до пересечения с кумулятой и опустив второй перпендикуляр из этой точки на ось абсцисс получаем, что численное значение медианы равно 24 см.

В курсовой работе произвести расчёт средней арифметической взвешенной, моду и медиану по представленным формулам. Медиану определить и графическим способом. Кумуляту построить на отдельном листе миллиметровой бумаги, формата А4.

1.2.5 Расчёт показателей скошенности и крутизны рада распределения

Показателем, характеризующим меру скошенности ряда распределения

является асимметрия. Она отражает меру отклонения распределения частот от симметричного их распределения относительно максимальной ординаты. Скошенность (асимметрия) ряда может быть левосторонней и правосторонней. Степень асимметрии можно определить несколькими способами:

1. используя численные значения моды или медианы;

2. используя отношение кубического отклонения вариант от средней величины и куба среднеквадратического отклонения;

3. используя моменты эмпирического распределения ряда.

Дата добавления: 2015-06-04