
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Расчет теоретических частот для кривой нормального распределения
|
|
|
|
Теоретические законы распределения случайных величин
Этот тип непрерывного распределения, открытого в 1733 г. Муавром, имеет плотность распределения:

где x - среднее значение;
σ - стандартное отклонение.
Графически плотность распределения F(x) представляет собой симметричную относительно точки х = x колоколообразную кривую, форма которой зависит от величины среднеквадратического отклонения, которое является параметром масштаба, а положение определяется значением средней.
Для расчета теоретических частот эмпирического ряда используют таблицы значений F(t), составленные для нормированного отклонения, которое рассчитывается по формуле:
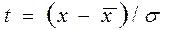
Расчет теоретических частот эмпирического ряда производят следующим образом:
1. Находят значение функции плотности вероятности нормального распределения через величину нормированного отклонения по приложению учебника.
2. Вычисляют теоретические частоты ряда распределения n, по соответствующим данным объема выборки при величине классового промежутка по формуле:
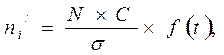
где n – объем выборки; С – классовый интервал; σ – стандартное отклонение; f (t) – плотность вероятности нормального распределения (ордината кривой нормального распределения).
Пример расчета теоретических частот для кривой нормального распределения приведен в таблице.
Таблица 2.1 Вычисление выравнивающих частот по уравнению Лапласа – Гаусса
| Классы, (групповые варианты) хi, см | Эмпирическая частота, ni, шт. | Отклонение, 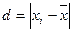 , см , см
| Нормированное отклонение,

| Плотность вероятности нормального распределения F(t) | Теоретическая частота, n/i, шт. | |
| фактическая | округленная | |||||
| 16,88 | 2,27 | 0,03034 | 1,63 | |||
| 12,88 | 1,73 | 0,08938 | 4,80 | |||
| 8,88 | 1,19 | 0,19652 | 10,55 | |||
| 4,88 | 0,66 | 0,32086 | 17,23 | |||
| 0,88 | 0,12 | 0,39608 | 21,27 | |||
| 3,12 | 0,42 | 0,36526 | 19,61 | |||
| 7,12 | 0,96 | 0,25164 | 13,51 | |||
| 11,12 | 1,49 | 0,13147 | 7,06 | |||
| 15,12 | 2,03 | 0,05082 | 2,73 | |||
| 19,12 | 2,57 | 0,01468 | 0,79 | |||
| Сумма |
- в первый столбец вписаны классовые варианты – xi,см;
- во втором столбце – эмпирическая частота ni,шт.;
- в третьем столбце центральное отклонение 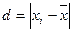 , см;
, см;
- в четвертом столбце – нормированное отклонение, показывающее,
насколько «σ» отдельные члены данной совокупности отклоняются от среднего уровня учитываемого признака. Нормированное отклонение рассчитывается по формуле:
 ,
,
где xi – групповая варианта;  – средняя величина; σ – стандартное отклонение;
– средняя величина; σ – стандартное отклонение;
- в пятом столбце – значение функции для нормированного отклонения – f(t);
- в шестом столбце – теоретически рассчитанная частота – n,, штук.
Например:
 .
.
Далее графически изображается распределение эмпирических и теоретических частот по классам. Для этого по оси абсцисс откладываются классы или групповые варианты, а по оси ординат частоты классов.
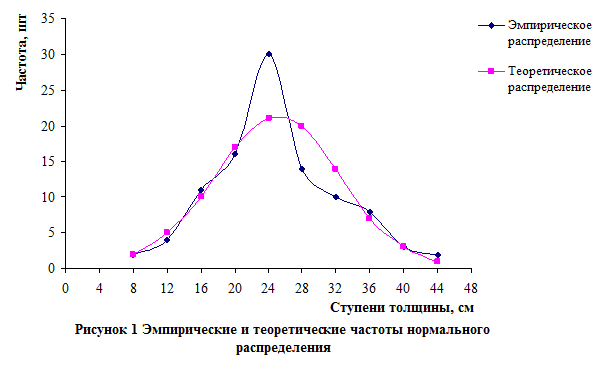
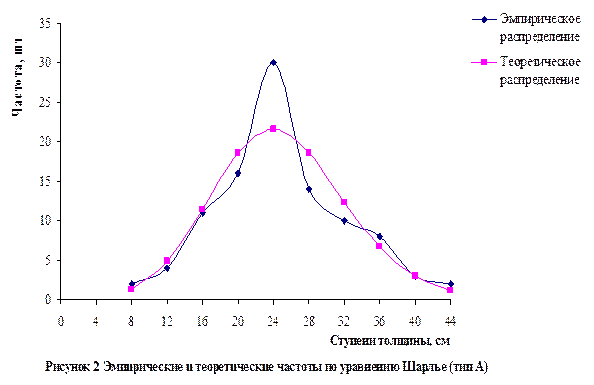
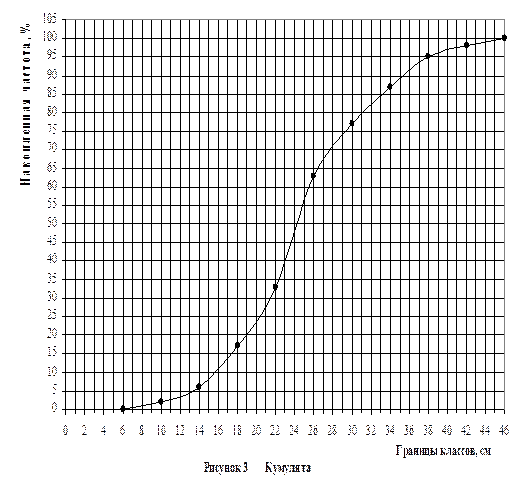

|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 4029; Нарушение авторских прав?; Мы поможем в написании вашей работы!