Статистическое сравнение двух выборочных средних

по t – критерию Стьюдента при равнозначных выборках

Критерий t-Стьюдента используется для оценки достоверности различий средних значений выборочных совокупностей. Фактическое значение критерия определяют по формуле:

t = ,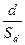

где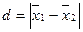

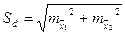
d – разность между сравниваемыми средними

S_d – ошибка разности средних

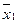и 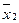_– значение сравниваемых средних выборочных совокупностей

m_x1² и m_x2²- значение ошибок средних выборочных совокупностей.

Данная формула применяется для сравнения средних выборочных совокупностей с равнозначным объёмом; то есть n₁= n_2, где n₁и n_{2 –} объем сравниваемых выборочных совокупностей.

Пример расчёта t-критерия фактического приведён в таблице 3.4.

Таблица 3.4 Статистическое сравнение двух выборочных средних по t- критерию Стьюдента

Фамилия	Объём выборки n, шт	Средняя величина x, мм	Ошибка средней mx, мм	tфакт	t 05/01
Иванов		31,08	0,85	12,43	2,05/2,76
Смирнов		47,30	0,99

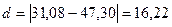
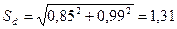
t_{факт =}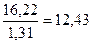

Фактическое значения t- критерия (t_ф) сравнивается с t_St на1% и 5%-ном уровне значимости, которые определяются с использованием приложения учебника (Герасимов, Хлюстов). Причём число степеней свободы устанавливается по формуле: k=n – 1.

Для приведенного примера k=30 – 1=29, следовательно, t _{05/ 01} = 2,05/2,76.

Так как t_ф (8,84) больше t₀₁, Н₀- гипотеза отвергается, различия между средними существенные.

В курсовой работе произвести сравнительную оценку со средними пятерых студентов (все данные представить в виде одной таблицы).

Статистическое заключение

В результате сравнения выборочной средней Иванова со средней Смирнова делаем заключение о существенности различий между ними, т.к фактическое значении t критерия больше t на 1 % уровне значимости.

( в курсовой работе отметить с кем выявлены существенные, а с кем несущественные различия)

Дата добавления: 2015-06-04