Графическая форма представления комплексных чисел

Для графического представления комплексных чисел применяют прямо-

угольную систему координат. В обычной (школьной) системе координат вдоль осей «х» (ось абсцисс) и «y» (ось ординат) откладываются положительные или отрицательные вещественные числа.

В системе же координат, принятой в символическом методе, вдоль оси «х»

в виде отрезков откладывают действительные числа, а вдоль оси «у» – мнимые

(рис. 1).

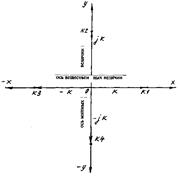
Рис. 1. Система координат для графического изображения комплексных чисел

Поэтому ось абсцисс «х» называют осью вещественных величин или, для сокращения, вещественной осью.

Ось ординат называют осью мнимых величин или мнимой осью.

Саму же плоскость (т.е. плоскость рисунка), на которой изображают комплексные числа или величины, называют комплексной плоскостью.

В этой плоскости комплексное число А = L + j М изображено вектором А

(рис. 2), проекция которого на вещественную ось равна его вещественной части Re A = А' = L, а проекция на мнимую ось – мнимой части Im A = А" = М.

(Re – от англ. real – реальный, действительный, настоящий, Im – от англ.imaginary – нереальный, мнимый).

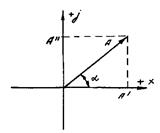
Рис. 2. Графическое представление комплексного числа

В этом случае число А можно записать так

А = А' + А" = Re A + j Im A (3).

Используя графическое изображение числа А в комплексной плоскости, введем новые определения и получим некоторые важные соотношения:

1. длина вектора А называется модулем вектора и обозначается |A|.

По теореме Пифагора

|A| = 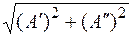(4).

2. уголα, образованный вектором А и вещественной положительной полу-

осью, называется аргументом вектора А и определяется через его тангенс:

tg α = А" / А' = Im A / Re A (5).

Таким образом, для графического представления комплексного числа

А = А' + А" в виде вектора надо:

1. найти модуль вектора |A| по формуле (4);

2. найти аргумент вектора tg α по формуле (5);

3. найти угол α из соотношения α = arc tg α;

4. в системе координат j (х) провести под углом α вспомогательную

прямую и на ней в определенном масштабе отложить отрезок, равный модулю вектора |A|.

Пример 2. Комплексное число А = 3 + j 4 представить в графической форме.

Решение:

1. модуль числа А

|A| = 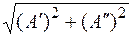= = 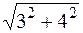= 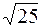5

2. аргумент числа

tg α = А" / А' = 4 / 3 = 1, 33

3. угол α = arc tg α = arc 1,33 = 53º 03' ≈ 53º

4. в системе координат j (х) проводим под углом α вспомогательную

прямую и на ней в масштабе μ = 1 А / см отложить отрезок длиной 5 см, равный модулю вектора |A|.

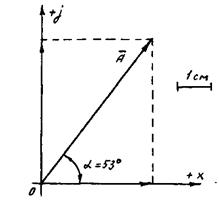
Рис. 3. Комплексное число А = 3 + j 4, представленное в графическом виде

(в виде вектора).

При необходимости из рис. 2 можно найти другие тригонометрические функции:

sin α = А" / |А|, отсюда А" = |А| sin α (6)

cos α = А' / |А|, отсюда А' = |А| cos α (7).

Выражения (6) и (7) будут использованы ниже при объяснении тригоно-

метрического изображения комплексных чисел.

Дополним тему «Графическая форма представления комплексных чисел»

исследованием роли мнимой единицы при графическом изображении комплексных

чисел.

Дата добавления: 2015-06-30