Тригонометрическая форма представления комплексных чисел

Чисел

Роль мнимой единицы при графическом изображении комплексных

В системе координат j (х) важную роль играет мнимая (отрицательная) единица j = .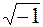

Поясним сказанное на примере.

Пусть имеется положительное действительное число «К». Отложим это число вдоль положительной полуоси «+х» (рис. 1).

Если это число умножить на мнимую единицу «j», то получится новое, уже мнимое число К' = j К. Это число надо отложить вдоль положительной полуоси «+j», т.е. вверх.

Если мнимое число «j К» еще раз умножить на мнимую единицу «j», то получится очередное новое число К'' = j* j К = j 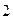К = (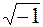) 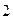*К = (- 1) К = - К.

Это новое число – отрицательное действительное, которое надо отложить вдоль отрицательной полуоси «- х», т.е. влево.

Третье умножение числа К на j дает отрицательное мнимое число К"' =

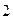= j (j К) = j К = j 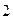(j К) = (- 1)* j К = - j К. Это число надо отложить вдоль отрицательной полуоси «- j», т.е. вниз.

При четвертом таком умножении числа К на j получается число К'''', равное исходному числу К:

К'''' = (j) (j )К = j 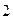= (j )*(j 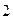)К = (- 1)*(- 1)К = К.

Из сказанного можно сделать 2 вывода:

1. мнимая единица j представляет собой поворотный множитель, при умножении

на который вектор, выражающий вещественное или мнимое число, поворачивается на 90º против направления движения часовой стрелки, т. е. в положительную сторо-

ну направления вращения векторов;

2. при умножении на мнимую единицу вещественное число превращается в мни-

мое, а мнимое число – в вещественное.

Для получения тригонометрической формы представления комплексных чисел используем графическую форму.

Как видно на рис. 2, А = А' + j А".

Подставим в правую часть этого уравнения выражения (6) и (7), тогда

А = |А| cosα + j |А| sinα = |А| (cosα + j sinα) (8)

Как следует из выражения (8), в правой его части находятся тригонометри-

ческие функции - cosα и sinα. Этим и объясняется название формы представления комплексного числа.

Таким образом, для тригонометрического представления комплексного числа А = А' + А" надо:

1. найти модуль вектора |A| по формуле (4);

2. найти аргумент вектора tg α по формуле (5);

3. найти угол α из соотношения α = arc tg α;

4. записать комплексное число в тригонометрической форме.

Пример 3. Комплексное число А = 3 + j4 представить в тригонометрической форме.

Решение:

1. модуль числа А

|A| = 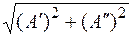= = 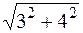= 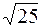5

2. аргумент числа

tg α = А" / А' = 4 / 3 = 1, 33

3. угол α = arc tg α = arc 1,33 = 53º 03' ≈ 53º

4. комплексное число в тригонометрической форме

А = |А| (cosα + j sinα) = 5 (cos 53º + j sin53º).

Дата добавления: 2015-06-30