
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Роль поворотного множителя при графическом изображении комплексных чисел
|
|
|
|
Показательная форма представления комплексных чисел
Для представления комплексных чиселв показательной форме используем формулу Эйлера
е 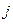 = (cosα + j sinα) (9),
= (cosα + j sinα) (9),
где: е = 2,73 – основание натуральных логарифмов;
cosα = Re е 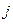 - действительная часть выражения е
- действительная часть выражения е 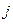 ;
;
sinα = Im е 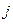 - мнимая часть выражения е
- мнимая часть выражения е 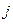 .
.
В этом случае выражение (8) можно записать так:
А = |А| (cosα + j sinα) = |А| е 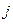 (10).
(10).
Таким образом, для представления комплексного числа в показательной форме надо:
1. найти модуль вектора |A| по формуле (4);
2. найти аргумент вектора tg α по формуле (5);
3. найти угол α из соотношения α = arc tg α;
4. записать комплексное число в показательной форме.
Пример 4. Комплексное число А = 3 + j4 представить в показательной форме.
Решение:
1. модуль числа А
|A| = 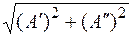 =
= 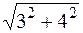 =
= 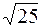 = 5
= 5
2. аргумент числа
tg α = А" / А' = 4 / 3 = 1, 33
3. угол α = arc tg α = arc 1,33 = 53º 03' ≈ 53º
4. комплексное число в показательной форме А = 5 е 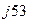 .
.
Выражение е 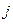 называется поворотным множителем и обозначает, что
называется поворотным множителем и обозначает, что
вектор, изображающий комплексное число |А| е 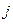 , повернут относительно вещественной полуоси «х» на угол α против направления движения часовой стрелки. Отрицательному значению угла α соответствует поворот вектора по часовой стрелке.
, повернут относительно вещественной полуоси «х» на угол α против направления движения часовой стрелки. Отрицательному значению угла α соответствует поворот вектора по часовой стрелке.
Показатель степени «j α» в выражении е 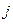 должен быть отвлеченным числом. Это означает, что угол «α» в выражении «j α» должен быть выражен в радианах. Однако ради большей наглядности допускается запись угла «α» в градусах.
должен быть отвлеченным числом. Это означает, что угол «α» в выражении «j α» должен быть выражен в радианах. Однако ради большей наглядности допускается запись угла «α» в градусах.
При расчетах электрических цепей встречаются случаи вычислений с поворотным множителем, результаты которых полезно запомнить:
1. е 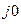 = cos 0 + j sin0 = 1 + 0 = 1;
= cos 0 + j sin0 = 1 + 0 = 1;
2. е 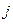 = е
= е 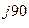 = cos (π / 2) + j sin(π / 2) = 0 + j*1 = j;
= cos (π / 2) + j sin(π / 2) = 0 + j*1 = j;
3. е 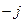 = е
= е 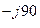 = cos (- π / 2) + j sin(- π / 2) = 0 - j*1 = -j;
= cos (- π / 2) + j sin(- π / 2) = 0 - j*1 = -j;
4. е 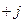 = е
= е 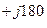 = (е
= (е 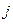 )
) 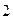 = (j)
= (j) 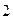 = - 1.
= - 1.
Таким образом, в результате умножения комплексного числа на поворотный множитель е 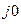 положение вектора, изображающего комплексное число, не изменя
положение вектора, изображающего комплексное число, не изменя
ется, во втором случае направление вектора совпадает с направление полуоси «+j»
(т.е. вектор расположен вверх), в третьем случае вектор расположен вниз, в четвертом случае вектор в результате умножения поворачивается на 180º против часовой стрелке (при + 180º) или по часовой (при - 180º).
В последнем случае направление поворота не имеет значения, т.к. при повороте как против часовой, так и по часовой стрелке, вектор занимает положение, противо
положное исходному.
В конце объяснения представим одно и тоже число А в разных формах:
1. в алгебраической А = 3 + j4;
2. в графической – в виде вектора на рис.2;
3. в тригонометрической А = 5 (cos 53º + j sin53º);
4. в показательной А = 5 е 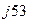 .
.
Таким образом, из четырех форм записи комплексного числа А только две –
алгебраическая и тригонометрическая, строго соответствуют понятию «комплекс-
ное число», т.е. такое число, которое состоит из нескольких частей.
Следует отметить, что при расчетах электрических цепей символическим методом часто приходится переходить от одной формы представления комплекс-
ного числа к другой, например, от алгебраической к показательной. Для таких переходов применяют простейшие действия над числами, а именно: сложение, вычитание, умножение и деление.
|
|
|
|
|
Дата добавления: 2015-06-30; Просмотров: 791; Нарушение авторских прав?; Мы поможем в написании вашей работы!