ПРИМЕР. Дано:кинематическая схема механизма и угловая скорость w1 = 0, угловое ускорениеε1

Дано: кинематическая схема механизма и угловая скорость w ₁ = 0, угловое ускорение ε ₁.

Определить: линейные и угловые ускорения.

Решение: Порядок определения ускорений:

О → А → D → В.

Для примера рассмотрим последовательность определения ускорений кинематических пар О и А:

Ускорение кинематической пары 0,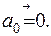

Ускорение пары А равно:

.

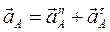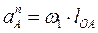– нормальное ускорение;

– тангенциальное (касательное) ускорение;

Рис. 22. План ускорений

Вектор нормального ускорения 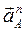направлен параллельно звену 1 (отрезку ОА) к центру его вращения О. Вектор касательного ускорения 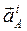направлен перпендикулярно звену 1 (отрезку ОА) в сторону его углового ускорения (по направлению ).

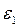Выбираем полюс ускорений р_а и строим вектор 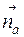, соответствующий нормальному ускорению 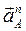, длина которого определяется: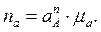

Из конца вектора 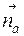строим вектор 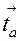, соответствующий тангенциальному ускорению 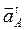длина которого равна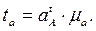

Соединив конец вектора 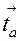с полюсом р_а, получим вектор абсолютного ускорения точки А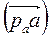 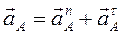или

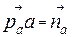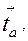+ отсюда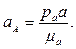

Строим нулевые векторы 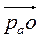и 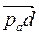на плане ускорений (точки О и d, совпадающие с полюсом ).

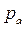По теореме подобия определяем и ускорения центров масс всех звеньев. Центр масс S₁ кривошипа 1 совпадает с осью его вращения 0, поэтому строим на плане ускорений точку s₁, совпадающую с точкой 0 и находим абсолютное ускорение точки S₁ .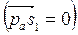

.

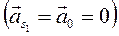Центр масс S₂ шатуна 2 находится в точке пересечения медиан треугольника ΔАВС, поэтому точку s₂ на плане ускорений строим в точке пересечения медиан треугольника Δаbc. Соединив ее с полюсом p_a, получим вектор абсолютного ускорения точки S₂ .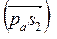

.

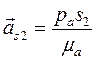Центр масс S₃ ползуна 3 совпадает с вращательной парой В. Построив на плане ускорений точку s₃, совпадающую с точкой b, получим вектор абсолютного ускорения точки S₃ ().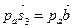

.

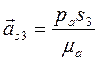Определим угловые ускорения всех звеньев механизма. Угловое ускорение ε₁ кривошипа 1 задано. Угловое ускорение ε₂ шатуна 2 найдем по выражению:

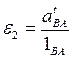или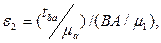

где .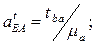

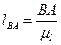Это угловое ускорение направлено против хода часовой стрелки, так как вектор тангенциального относительного ускорения 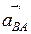(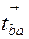) стремится повернуть точку В относительно точки А на звене 2 против часовой стрелки. Угловое ускорение ε₃ ползуна 3 равно нулю, так как он совершает поступательное движение:

ε₃ = 0.

Дата добавления: 2015-06-30