ВВЕДЕНИЕ. 1. Сопротивление материалов : учеб

А. В. Кириллов

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Сопротивление материалов: учеб. для техн. вузов / Г. С. Писаренко – Киев: Вища школа, 1986. – 389 с.

2. Руководство к решению задач по сопротивлению материалов: учеб. пособие для вузов / Г. М. Ицкович [и др.] – М.: Высшая школа, 1999. – 592 c.

3. Манжосов В. К. Прикладная механика: учеб. пособие / В. К. Манжосов. – Ульяновск: УлГТУ, 2007. – 256 с.

4. Теория механизмов и машин: учеб. пособие для вузов / А. И. Смелягин – М.: Новосибирск: Инфра-М: НГТУ, 2007. – 262 с.

5. Детали машин: учебник / В. А. Вагнер – Барнаул, 2007. – 743 с.

6. Чернилевский Д. В. Детали машин и основы конструирования: учебник для вузов. - М.: Машиностроение, 2006. – 655 с.

СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ.
РЕШЕНИЕ ЗАДАЧ

Утверждено Редакционно-издательским советом НГПУ

в качестве учебного пособия

Новосибирск
2007

УДК 539.2/.6(075.8) Печатается по решению

ББК 30.12 я 73-4 Редакционно-издательского совета НГПУ

К-431

Научный редактор –

кандидат технических наук, профессор,

зав. кафедрой машиноведения НГПУ

В.М. Потапов

Рецензенты:

доктор технических наук, профессор

кафедры механики НТИ МГУДТ

А.М. Красюк;

доктор технических наук, профессор,

зав. кафедрой «Материаловедение в машиностроении» НГТУ

А.А. Батаев

К-431 Кириллов, А.В. Сопротивление материалов. Решение задач: учебное пособие /А. В. Кириллов. – Новосибирск: Изд. НГПУ, 2007. – 138 с.

Настоящая работа является руководством к решению студентами практических задач по курсу «Сопротивление материалов». Основное содержание пособия – примеры решения типовых задач, снабженные необходимыми теоретическими сведениями, варианты домашних заданий и контрольных работ, а также вопросы для самопроверки после каждого раздела.

Пособие предназначено для студентов, обучающихся по специальностям «Профессиональное обучение» (машиностроение и технологическое оборудование; автомобили и автомобильное хозяйство), «Технология и предпринимательство» и «Сервис».

УДК 539.2/.6(075.8)

ББК 30.12 я 73-4

© Кириллов А.В., 2007

© ГОУ ВПО «Новосибирский государственный педагогический университет», 2007

Предлагаемое учебное пособие написано в соответствии с Государственными образовательными стандартами по специальностям 030500.8 «Профессиональное обучение (машиностроение и технологическое оборудование)» (специализация 030501.08 «Технология и оборудование машиностроения»); 050501.15 «Профессиональное обучение (автомобили и автомобильное хозяйство)»; 030600 «Технология и предпринимательство» (специализации 030619 «Конструирование и моделирование одежды» и 030601 «Техника и техническое творчество»); 230700 «Сервис» (специализации 230712 «Автосервис» и 230708 «Сервис бытовых машин и приборов»).

Основная цель пособия – изучение и закрепление теоретического материала по дисциплине «Сопротивление материалов» в ходе выполнения студентами домашних заданий и контрольных работ, приобретение навыков при решении практических задач. В процессе усвоения курса и приобретения определенных навыков, а также выполнения домашних заданий, контрольных и лабораторных работ студенты должны получить представление о методах, применяемых при расчетах на прочность и жесткость при различных видах деформаций как для статически определимых, так и статически неопределимых систем.

Порядок изложения решения рассмотренных типовых задач соответствует расположению учебного материала в общем курсе «Сопротивление материалов», а их содержание и направленность – практическому усвоению и закреплению теоретических знаний при изучении этой дисциплины.

Пособие адресовано студентам факультета «Технологии и предпринимательства».

1. РАСЧЕТЫ НА ПРОЧНОСТЬ И ЖЕСТКОСТЬ ПРИ
ОСЕВОМ РАСТЯЖЕНИИ-СЖАТИИ

Построение эпюр продольных сил. Растяжение-сжатие – простейший вид деформаций, при котором внешние силы приложены вдоль продольной оси бруса, а в поперечном сечении его возникает только продольная (нормальная) сила.

Расчеты на прочность и жесткость при растяжении-сжатии начинаются с построения эпюры продольной силы с помощью универсального метода сечений, применяемого для построении эпюр внутренних силовых факторов [1 – 7, 9, 11]. Сущность этого метода заключается в следующем:

· рассекаем элемент конструкции плоскостью, перпендикулярной продольной оси;

· отбрасываем часть конструкции, лежащую по одну сторону от сечения;

· заменяем действие отброшенной части внутренним силовым фактором, соответствующим виду деформаций, который направляем в соответствии с принятым правилом знаков;

· составляя уравнение равновесия оставшейся части, находим искомый внутренний силовой фактор в виде функции от координаты сечения.

Продольная сила численно равна сумме проекций, приложенных к одной из отсеченных частей внешних сил на ось стержня (для прямолинейного стержня она совпадает в каждом сечении с осью Oх). Растяжение (сжатие) имеет место, если все внешние силы, действующие по одну сторону от данного поперечного сечения, сводятся к равно­действующей, направленной вдоль оси стержня (рис. 1.1 и 1.2). Одна и та же продольная сила N при действии на различные части стержня (левую или правую) имеет противоположные направления. Знак N зависит от характера вызываемой ею деформации. Продольная сила считается положительной, если вызывает растяжение элемента, и отрицательной, если вызывает сжатие.

На основе данных расчета, произведенного методом сечений, строится эпюра нормальных сил в виде графика распределения нормальной силы по длине бруса (задача 1). Характерно, что скачки на эпюре обусловлены наличием в соответствующих сечениях сосредоточенных сил, что, в свою очередь, может служить доказательством правильности выполненных построений.

Напряжения при растяжении-сжатии. Расчет на прочность. Так как при растяжении-сжатии в сечении элемента возникает только продольная сила, вектор которой направлен перпендикулярно плоскости поперечного сечения, то в этом сечении возникают только нормальные напряжения. Закон распределения этих напряжений вытекает из гипотезы плоских сечений, подтвержденной экспериментальными данными. Представим себе стержень, изготовленный из какого-либо податливого материала, на боковую поверхность которого нанесена система продольных и поперечных рисок (рис. 1.1, а). Эта ортогональная система рисок остается таковой и после приложения растягивающей нагрузки (рис. 1.1, б). Поперечные риски являются следами поперечных сечений на поверхности стержня и остаются прямыми и перпендикулярными к оси стержня, это свидетельствует о выполнении гипотезы плоских сечений (Бернулли). С учетом гипотезы об отсутствии поперечного взаимодействия продольных волокон приходим к выводу, что деформация растяжения стержня сводится к одноос­ному растяжению его продольных волокон, и в поперечном сечении стержня возникают лишь нормальные напряжения σ (рис. 1.2). Ортогональность продольных и поперечных рисок свидетельствует также об отсутствии сдвигов, а, следовательно, и связанных с ними касательных напряжений τ в поперечных и продольных сечениях стержня.

Рис.1.1. Модель растянутого стержня

Рис.1.2. Связь напряжения и усилия

Тогда продольная сила N, равная сумме проекций внутренних сил, действующих в данном поперечном сечении площадью А (рис. 1.2), очевидно, будет равна:

(1.1)

Это соотношение является уравнением равновесия (статики), связывающим продольную силу N и нормальное напряжение σ, которое в общем случае является функцией координат z и у и поэтому не может быть найдено из одного лишь уравнения статики. Таким образом, задача определения напряжений даже в самом простом случае деформирования стержня (растяжении или сжатии) оказывается статически неопределимой.

Необходимое для решения этой задачи дополнительное уравнение вытекает из гипотезы плоских сечений. Поскольку поперечные сечения стержня, оставаясь плоскими и перпендикулярными к оси стержня, в процессе деформирования лишь поступательно перемещаются вдоль оси стержня (что приводит к одинаковому удлинению всех продольных волокон), приходим к уравнению ε = const (ε – относительное удлинение), что следует из закона Гука для линейно упругого материала:

, (1.2)

откуда получим

. (1.3)

Таким образом, при растяжении (сжатии) призматического стержня нормальные напряжения равномерно распределены по поперечному сечению, а касательные напряжения в сечениях отсутствуют, что является следствием гипотезы плоских сечений. Указанное, несмотря на, казалось бы, очевидность и простоту, является фундаментальным результатом, справедливым, строго говоря, лишь для призматического стержня. Однако в инженерной практике его используют и для приближенной оценки нормальных напряжений в стержнях переменного сечения. При этом, чтобы погрешность формулы была невелика, необходимо, чтобы площадь поперечного сечения стержня изменялась достаточно плавно вдоль его оси.

Условие прочности при растяжении (сжатии) призматического стержня для стержня из пластического материала (т. е. материала, одинаково работающего на растяжение и сжатие) будет иметь вид:

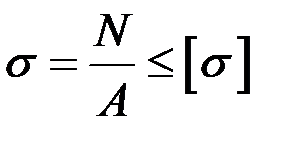, (1.4)

где – допускаемое напряжение.

Продольная сила N в условии (1.4) подставляется по модулю, так как знак в этом случае роли не играет. Для стержней из хрупких материалов, неодинаково сопротивляющихся растяжению и сжатию, знак напряжения имеет принципиальное значение, и условие прочности приходится формулировать отдельно для растяжения и сжатия:

,

,

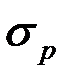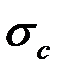где и – напряжения растяжения и сжатия, а и 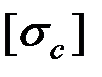– соответствующие им допускаемые напряжения.

В практике инженерных расчетов, исходя из условия прочности, решаются три основные задачи механики материалов конструкций. В применении к случаю растяжения (сжатия) призматического стержня эти задачи формулируются следующим образом.

Проверка прочности (поверочный расчет). Этот расчет проводится, если нагрузка (в нашем случае ее представляет N), сечение стержня A и его материал (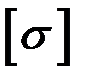) заданы.

Необходимо убедиться, что выполняется условие прочности (1.4). Проверочный расчет заключается в том, что определяется фактический коэффициент запаса прочности п и сравнивается с нормативным коэффициентом запаса [ n ]:

, (1.5)

где 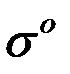– предельное (или опасное) напряжение, т. е. напряжение, вызывающее отказ элемента конструкции (напомним, что, например, для стержня из пластичного материала это предел текучести или условный предел текучести ).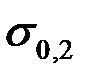

Подбор сечения (проектный расчет). В этом расчете по заданной нагрузке определяются размеры поперечного сечения стержня из заданного материала ([ ] дано). Минимальное значение A получим, если в условии прочности (1.4) принять знак равенства:

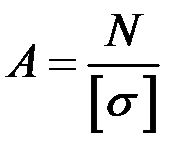. (1.6)

Определение допускаемой нагрузки, то есть максимального значения нагрузки, которое допускает данный элемент конструкции (А и даны) при выполнении условия прочности:

. (1.7)

Определение деформаций и перемещений. Определим упругие деформации стержня, предполагая, что изменение его длины при растяжении , называемое абсолютной продольной деформацией или удлинением, мало́ по сравнению с его первоначальной длиной. Тогда относительная продольная деформация будет равна:

. (1.8)

Учитывая, что, согласно закону Гука, для одноосного растяжения (сжатия) из выражения (1.2) для абсолютной деформации получаем:

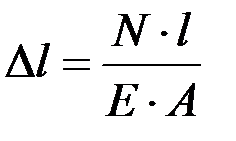. (1.9)

Произведение EA принято называть жесткостью поперечного сечения стержня при растяжении (сжатии), так как удлинение обратно пропорционально EA.

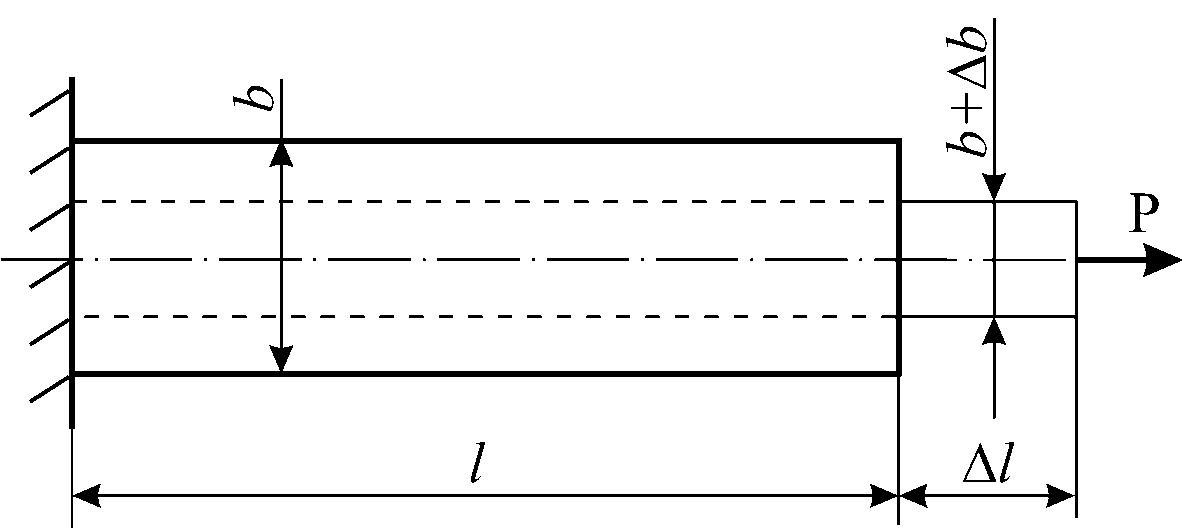
Рис.1.3. Модели продольной и поперечной деформаций

Как показывают эксперименты, при растяжении стержня размеры его поперечного сечения уменьшаются, а при сжатии – увеличиваются. Это явление получило название эффекта Пуассона.

По аналогии с продольной деформацией изменение размеров поперечного сечения (на рис. 1.3 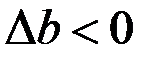) будем называть абсолютной поперечной деформацией, а – относительной поперечной деформацией. Относительные продольная и поперечная деформации, имеющие противоположные знаки, связаны между собой коэффициентом 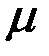, являющимся константой материала и называемым коэффициентом поперечной деформации или коэффициентом Пуассона:

. (1.10)

Как известно, для изотропного материала .

Формула (1.9) для удлинения стержня 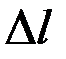применима только в случае, когда по длине стержня ни жесткость поперечного сечения, ни продольная сила не изменяются (EA = const, N = const). Удлинение стержня со ступенчатым изменением EA и N может быть определено как сумма удлинений ступеней, у которых EА и N постоянны:

, (1.11)

где индекс k у модуля продольной упругости означает, что участки стержня могут быть изготовлены из различных материалов.

ЗАДАЧА 1

Для ступенчатого стержня, расчетная схема которого показана на рис. 1.4, требуется: построить в выбранных масштабах эпюры внутренних усилий, нормальных напряжений и осевых перемещений; из условия прочности подобрать размеры поперечного сечения.

Дано: А₁/А₂ = 1,2; P₁ = 64 кН, P₂ = 42 кН, P₃ = 2,1 P₂,

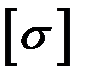= 160 МПа, Е МПа.

Решение

Дата добавления: 2015-06-30