Расчет на прочность балок при изгибе

Построение эпюр изгибающих моментов и поперечных сил. Плоский поперечный (прямой) изгиб – вид деформаций, при котором в поперечном сечении элемента действуют два внутренних силовых фактора: изгибающий момент и поперечная сила. Данный простой вид сопротивления реализуется в случае, когда внешние силы приложены перпендикулярно продольной оси бруса (балки) и расположены в одной из главных плоскостей в соответствии с конфигурацией поперечного сечения балки.

При прямом чистом изгибе в поперечном сечении стержня возникает только один силовой фактор – изгибающий момент М_z (рис. 3.1). Так как Q_y=dM_z / dz=0, то M_z=const, поэтому чистый прямой изгиб может быть реализован при загружении стержня парами сил, приложенными в торцевых сечениях стержня.

Рис.3.1. Связь внутреннего усилия и напряжения

Эпюры изгибающих моментов и поперечных сил строятся методом сечений (раздел 1) по участкам. Участком считается расстояние между сечениями, в которых действуют внешние силовые факторы (сосредоточенные силы и пары сил). Особо выделяются участки действия равномерно распределенной нагрузки. При построении эпюр в балках приняты следующие правила знаков:

· изгибающий момент считается положительным, если он стремится вызвать сжатие в верхних волокнах балки;

· поперечная сила считается положительной, если она стремится повернуть элемент по ходу часовой стрелки [1 – 7, 9 – 11].

Нормальные напряжения при чистом изгибе. Условие прочности. Поскольку изгибающий момент M_z по определению равен сумме моментов внутренних сил относительно оси Оz, то с нормальными напряжениями его связывает вытекающее из этого определения уравнение статики [1–7]:

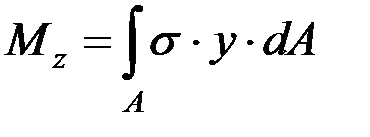. (3.1)

Для определения закона распределения нормальных напряжений по сечению проанализируем деформации модели стержня из низкомодульного материала, на боковой поверхности которого нанесена сетка продольных и поперечных рисок (рис. 3.2). Поперечные риски при изгибе стержня парами сил, приложенными в торцевых сечениях, остаются прямыми и перпендикулярными к искривленным продольным рискам, это позволяет сделать вывод о выполнении гипотезы плоских сечений, которая, как показывает решение этой задачи методами теории упругости, перестает быть гипотезой, становясь точным фактом – законом плоских сечений. Замеряя изменение расстояний между продольными рисками, приходим к выводу о справедливости гипотезы о ненадавливании продольных волокон .

Ортогональность продольных и поперечных рисок до и после деформирования (как отражение действия закона плоских сечений) указывает также на отсутствие сдвигов (касательных напряжений) в поперечных и продольных сечениях стержня.

Рис. 3.2. Модель чистого изгиба

Таким образом, чистый прямой изгиб призматического стержня сводится к одноосному растяжению или сжатию продольных волокон напряжениями . При этом часть волокон находится в зоне растяжения (на рис. 3.2 это нижние волокна), а другая часть – в зоне сжатия (верхние волокна). Эти зоны разделены нейтральным слоем (п – п), не меняющим своей длины, напряжения в котором равны нулю. Учитывая сформулированные выше предпосылки и полагая, что материал стержня линейно-упругий, т. е. закон Гука в этом случае имеет вид 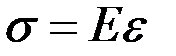, получены формулы для кривизны нейтрального слоя 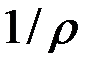( 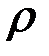– радиус кривизны) и нормальных напряжений . Предварительно отметим, что постоянство поперечного сечения призматического стержня и изгибающего момента (M_z=сonst), обеспечивает постоянство радиуса кривизны нейтрального слоя по длине стержня (рис. 3.3, а), нейтральный слой (п – п) описывается дугой окружности.

Рассмотрим призматический стержень в условиях прямого чистого изгиба (рис. 3.3, а) с поперечным сечением, симметричным относительно вертикальной оси Оу. Это условие не отразится на конечном результате (чтобы прямой изгиб был возможен, необходимо совпадение оси Оу с главной осью инерции поперечного сечения, которая и является осью симметрии). Ось Oz поместим на нейтральном слое, положение которого заранее неизвестно.

Рис. 3.3. Фрагмент чистого изгиба бруса: а) расчетная схема,
б) деформации и напряжения

Рассмотрим вырезанный из стержня элемент длиной dх, который в масштабе с искаженными в интересах наглядности пропорциями изображен на рис. 3.3, б. Поскольку интерес представляют деформации элемента, определяемые относительным смещением его точек, одно из торцевых сечений элемента можно считать неподвижным. Ввиду малости 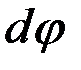считаем, что точки поперечного сечения при повороте на этот угол перемещаются не по дугам, а по соответствующим касательным.

Вычислим относительную деформацию продольного волокна АВ, отстоящего от нейтрального слоя на у:

.

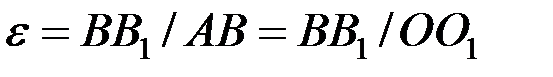Из подобия треугольников СОО₁ и О₁ВВ₁ следует, что

.

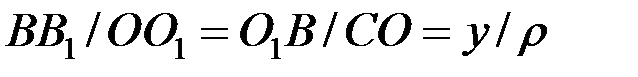Продольная деформация 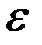оказалась линейной функцией расстояния от нейтрального слоя, что является прямым следствием закона плоских сечений:

. (3.2)

Тогда нормальное напряжение, растягивающее волокно АВ, согласно закону Гука, будет равно:

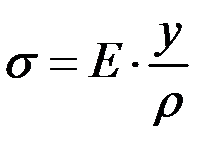. (3.3)

Эта формула не пригодна для практического использования, так как содержит две неизвестные: кривизну нейтрального слоя 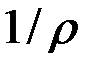и положение нейтральной оси Ох, от которой отсчитывается координата у.

Определим кривизну нейтрального слоя, подставляя (3.3) в (3.1):

, (3.4)

где 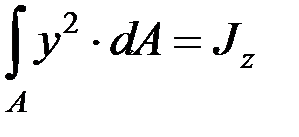, (3.5)

J_z – главный центральный момент инерции относительно оси О. Таким образом, для кривизны нейтрального слоя получаем формулу:

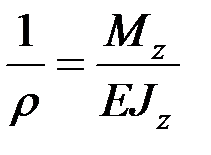. (3.6)

Кривизна нейтрального слоя 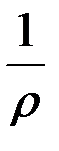является мерой деформации стержня при прямом чистом изгибе: 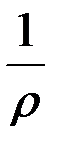тем меньше, чем больше величина EJ_z, называемая жесткостью поперечного сечения при изгибе (изгибной жесткостью – по аналогии с крутильной жесткостью 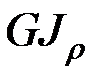и жесткостью поперечного сечения при растяжении-сжатии EA).

Подставляя (3.6) в (3.3), получаем формулу для нормальных напряжений в виде:

, (3.7)

которая была впервые получена Ш. Кулоном в 1773 г. Для согласования знаков изгибающего момента М_z и нормальных напряжений в правой части формулы (3.7) ставится знак минус, так как при M_z>0 нормальные напряжения при y >0 оказываются сжимающими. Однако в практических расчетах удобнее, не придерживаясь формального правила знаков, определять напряжения по модулю, а знак ставить по смыслу.

Таким образом, нормальные напряжения при чистом изгибе призматического стержня являются линейной функцией координаты у и достигают наибольших значений в волокнах, наиболее удаленных от нейтральной оси (рис. 3.4), т. е.

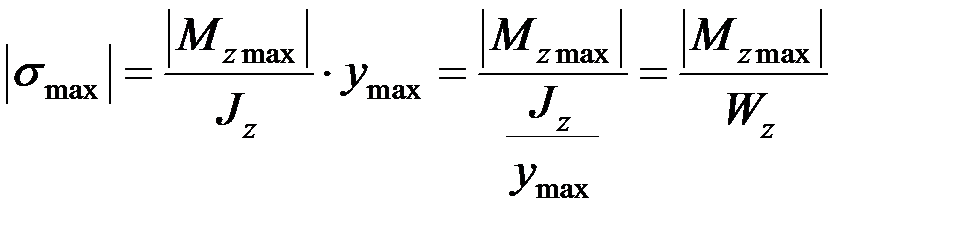. (3.8)

Рис.3.4. Распределение нормальных напряжений

Здесь введена геометрическая характеристика 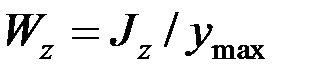, имеющая размерность м³ и получившая название момента сопротивления при изгибе. Поскольку при заданном M_z максимальные напряжения тем меньше, чем больше W_z, то момент сопротивления является геометрической характеристикой прочности поперечного сечения при изгибе.

Приведем примеры вычисления моментов сопротивления для простейших форм поперечных сечений. Для прямоугольного поперечного сечения (рис. 3.5, а) имеем J_z=bh³/12, y_max = h/2, тогда

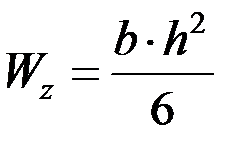. (3.9)

Аналогично для круга (рис. 3.5, a J_z = π d⁴ /64, y_max = d/2) получаем:

. (3.10)

Для кругового кольцевого сечения (рис. 3.5, в), получаем:

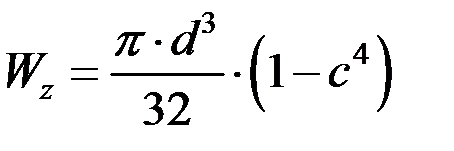, (3.11)

где .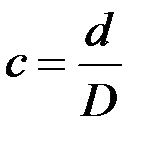

Рис. 3.5. Конфигурации поперечных сечений бруса

Итак, обобщая вышесказанное, поскольку ось z является нейтральной (рис. 3.5), максимальные нормальные напряжения в сечении с изгибающим моментом M_z определяются по формуле:

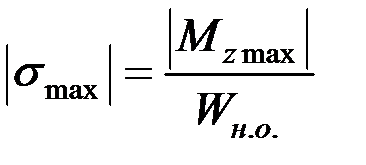. (3.12)

Этой формулой удобно пользоваться для расчета балок пластичного материала в упругой области, одинаково работающего на растяжение и сжатие. Поскольку знак напряжения в этом случае не имеет значения, напряжения вычисляются по модулю, и условие прочности при изгибе балки в форме призматического стержня принимает вид:

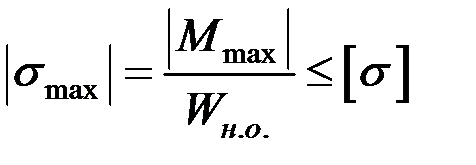, (3.13)

где 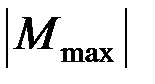– максимальное значение изгибающего момента (легко определяемое по его эпюре), 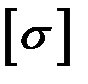– допускаемое напряжение на простое растяжение (сжатие). Напомним, что чистый изгиб балки сводится к растяжению и сжатию ее волокон (неравномерному в отличие от деформации растяжения (сжатия) призматического стержня, при котором ).

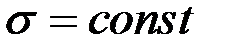Рис.3.6. Модель изгиба хрупкого материала

При расчете балок из хрупких материалов следует различать наибольшие растягивающие max 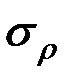и наибольшие сжимающие 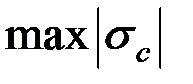напряжения (рис. 3.6), которые также определяются по модулю непосредственно и сравниваются с допускаемыми напряжениями на растяжение 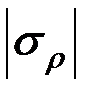и сжатие 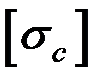. Условия прочности в этом случае будут иметь вид:

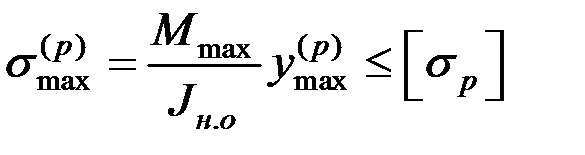, (3.14)

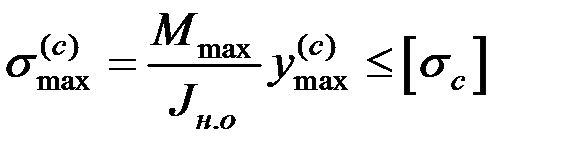. (3.15)

ЗАДАЧА 3

Для двухопорной балки требуется составить аналитические выражения поперечных сил Q и изгибающих моментов М по участкам, построить эпюры Q, М. Также необходимо из условия прочности по нормальным напряжениям определить размеры поперечного сечения балки заданной формы; определить нормальные и касательные напряжения в точке А поперечного сечения, для которого Q и М имеют наибольшие значения.

Дано: расчетная схема балки приведена на рис. 3.7, где q = 24 кН/м,

F = 38 кН, М₁ = 51 кН м; допускаемое напряжение 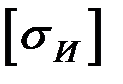= 100 МПа.

Решение

Дата добавления: 2015-06-30