
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Построение эпюр изгибающих моментов и поперечных сил
|
|
|
|
Определение опорных реакций.
Определяем реакции опор RA, RB. Для этого составляем уравнения статики, приравнивая к нулю суммы моментов относительно точек А и В:
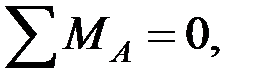
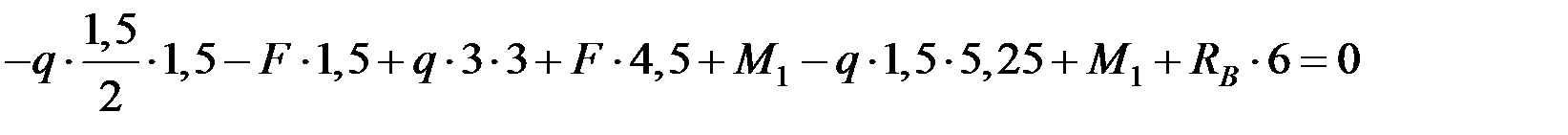 .
.
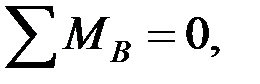
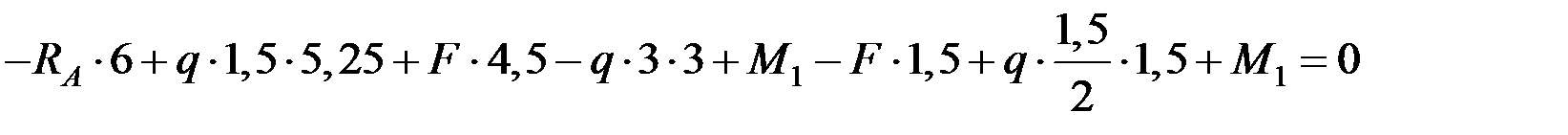 .
.
Отсюда находим 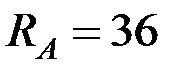 кН,
кН, 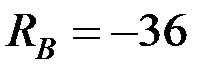 кН.
кН.
Реакция 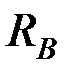 получилась со знаком минус, следовательно, в действительности она направлена вниз.
получилась со знаком минус, следовательно, в действительности она направлена вниз.
Рис. 3.7. Построение эпюр изгибающих моментов
и поперечных сил в балке
Проверка реакций: составляем уравнение статики, приравнивая к нулю сумму проекций всех сил на ось у.
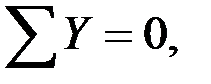
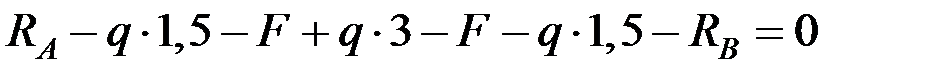 .
.
Уравнение удовлетворяется тождественно, следовательно, реакции определены правильно.
Составляем выражения поперечных сил и изгибающих моментов по участкам, пользуясь методом сечений и формулами:
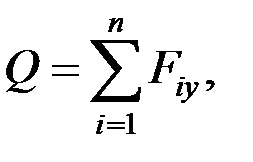
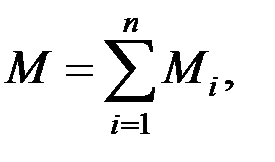
где 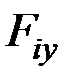 – проекции внешних сил, действующих на отсеченную часть;
– проекции внешних сил, действующих на отсеченную часть; 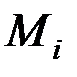 – моменты от нагрузки, действующей на отсеченную часть [1 – 3,7, 9, 14 – 19].
– моменты от нагрузки, действующей на отсеченную часть [1 – 3,7, 9, 14 – 19].
Правило знаков: 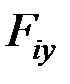 берутся с плюсом, если силы направлены по оси y, и с минусом, если направлены против оси y, правой декартовой системы координат;
берутся с плюсом, если силы направлены по оси y, и с минусом, если направлены против оси y, правой декартовой системы координат; 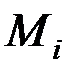 берётся с плюсом, если он изгибает балку относительно сечения выпуклостью вниз, и с минусом – при изгибе балки выпуклостью вверх (правило дождя) [1,2,3, 7 – 9].
берётся с плюсом, если он изгибает балку относительно сечения выпуклостью вниз, и с минусом – при изгибе балки выпуклостью вверх (правило дождя) [1,2,3, 7 – 9].
1-й участок: (0 < х 1< 1,5 м).
Рассматриваем левую отсеченную часть (рис.3.8)
Рис. 3.8. Расчетная схема левой отсеченной части на 1-м участке
Запишем уравнения для поперечных сил и изгибающих моментов:
Q = RA – q∙х1, M = RA х1 – q∙х1∙(х1/2).
Строим эпюры Q, М. Для этого вычисляем значения Q и М в начале и конце участка, а также в промежуточном сечении, соответствующем середине участка, при х 1 = 0,75 м:
Q(х1=0) = R1 = 36 кН, М (х1 = 0) = 0.
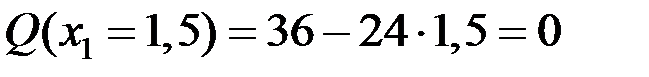 ,
, 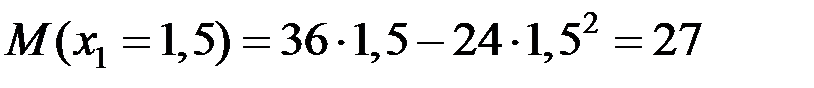 кН·м,
кН·м,
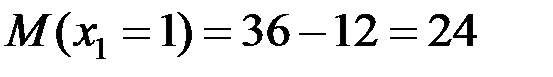 кН·м.
кН·м.
Эпюры M и Q приведены на рис. 3.7. Заметим, что эпюра выпуклостью направлена против направления действия распределенной нагрузки q (правило обтекания или правило дождя).
2-й участок: (0< х 2<3 м).
Расчетная схема изображается аналогично приведенной на рис. 3.8. Проводя сечение на расстоянии х 2 от левого края участка, получаем по формулам следующие результаты:
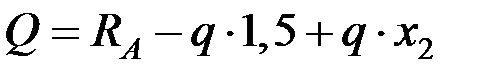 ,
,
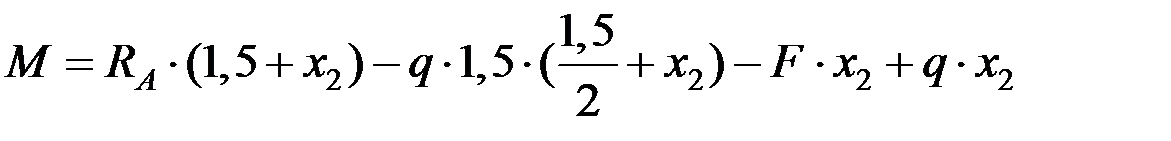 .
.
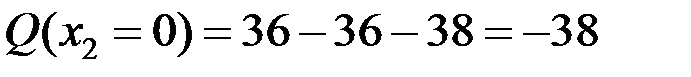 кН,
кН,
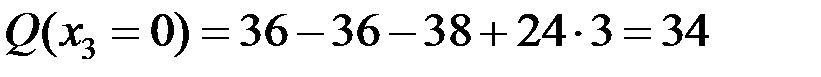 кН,
кН,
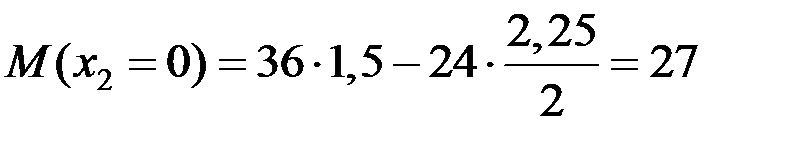 кН·м,
кН·м,
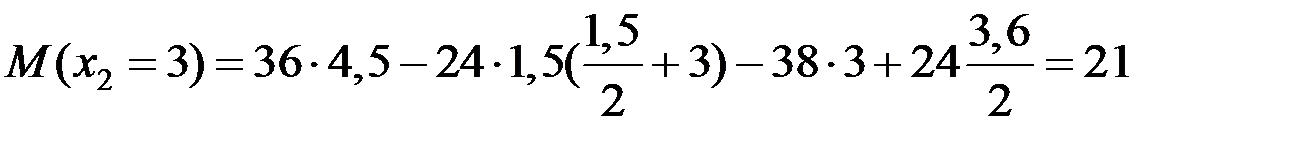 кН·м.
кН·м.
Эпюры M и Q для 2-го участка представлены на рис. 3.7. Заметим, что эпюра Q пересекает базу, т.е. на 2-м участке имеется такое сечение, в котором поперечная сила равна нулю. В соответствии с дифференциальной зависимостью
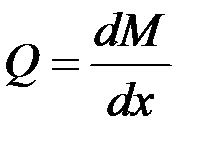
в этом сечении на эпюре М должен быть минимум (поперечная сила меняет знак с «–» на «+» (рис. 3.7) [1 – 9,11]. Приравнивая к нулю выражение для Q, находим х 2, при котором М имеет минимальное значение:
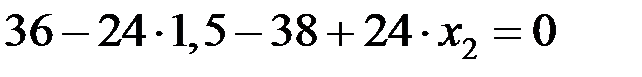 ,
,
откуда 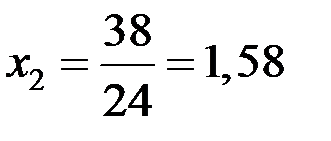 м
м
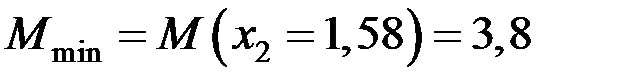 кН·м.
кН·м.
3-й участок: (0 < х 3 < 1,5 м).
На этом участке удобнее рассматривать правую отсеченную часть (рис. 3.9). Уравнения для изгибающих моментов и поперечных сил:
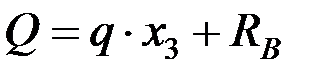 ,
,
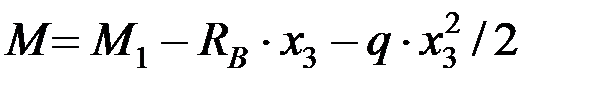 .
.
Рис.3.9. Расчетная схема правой отсеченной части на 3-м участке
Определим в характерных сечениях значение поперечных сил и изгибающих моментов:
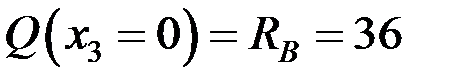 кН,
кН, 
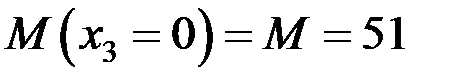 кН,
кН, 
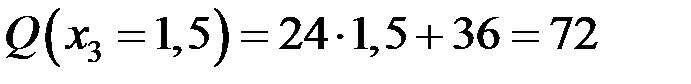 кН·м,
кН·м, 
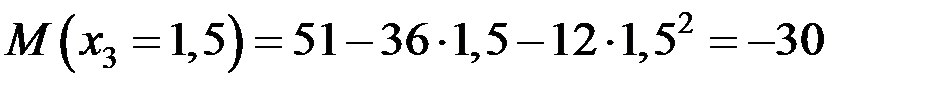 кН·м,
кН·м, 
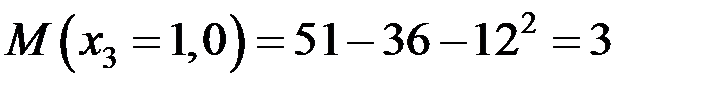 кН.
кН.
По данным расчета строим эпюры Q и M. Заметим, что скачки на эпюре Q равны сосредоточенным силам F, а на эпюре М – сосредоточенным моментам М (рис. 3.7).
|
|
|
|
|
Дата добавления: 2015-06-30; Просмотров: 520; Нарушение авторских прав?; Мы поможем в написании вашей работы!