Основные параметры оперативной обстановки на пожаре

Основными временными характеристиками процесса пожаротушения являются:

продолжительность следования первого пожарного подразделения к месту вызова;

время боевой работы (время с момента прибытия до отъезда с места пожара);

время тушения (занятости) пожарного подразделения (с момента выезда и до возвращения к месту дислокации).

Рассмотрим эти характеристики, связь между ними и их математическое описание.

Под временем тушения (занятости) пожарного подразделения понимается промежуток времени от момента выезда пожарного подразделения по вызову до момента его постановки в боевой расчет, т.е. до момента его готовности к следующему выезду после возвращения в пожарную часть
(τ_зан = τ_туш).

Этот промежуток времени является суммой нескольких менее продолжительных промежутков времени (рис. 2.1):

время тушения (занятости) τ_туш = t_гот – t_в;

время следования τ_след = t_пр – t_в;

время разведки и боевого развертывания τ_разв = t_н.т. – t_пр. (разведка производится с момента выезда до ликвидации пожара);

время локализации пожара τ_л = t_лок – t_н.т.;

время разборки конструкций и проливки τ_разб = t_ок.бр. – t_ликв. (возможно, что разборка производится и в период тушения);

время постановки в боевой расчет τ_б.р. = t_гот – t_возвр.;

время боевой работы τ_б = t_ок.бр. – t_пр.

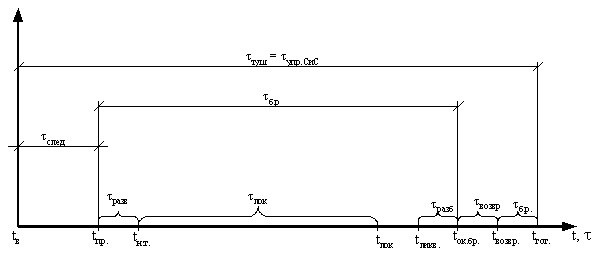
Рис.2.1. Временные характеристики процесса тушения пожара

Все указанные временные характеристики процесса пожаротушения являются непрерывными случайными величинами и могут быть описаны соответствующими функциями распределения и числовыми характеристиками (математическим ожиданием и дисперсией). В каждом конкретном случае тот или иной промежуток времени может быть равным нулю (например, время разборки и проливки при ликвидации загорания). В случае ложного или ошибочного вызова равны нулю все вышеперечисленные промежутки времени, кроме времени следования к месту вызова и обратно.

В любом случае время занятости (тушение) значительно больше времени боевой работы. Эту величину необходимо прежде всего знать для обоснования численности оперативных отделений пожарной охраны, а продолжительность подачи ОТВ необходима для обоснования запасов ОТВ (воды, пены, порошка и т.п.).

Время следования (время прибытия) является важной характеристикой эффективности оперативной деятельности пожарных подразделений.

Эти временные промежутки, характеризующие процесс пожаротушения, можно описать математически. Если найти функции распределения для каждого из перечисленных интервалов времени, то можно аналитически определить и функцию распределения времени занятости, поскольку она является суммой этих случайных величин.

Продолжительность боевой работы – это промежуток времени от момента введения сил и средств на пожаре (иными словами, от момента прибытия подразделения) до момента ликвидации пожара, т.е. выведения сил и средств. Теоретически она может принять любое значение от 0 до бесконечности.

Введем функцию распределения F(t) = P{t_p£t}, т.е. вероятность того, что продолжительность боевой работы будет меньше любого фиксированною значения t. Очевидно, что при t £0 имеем F(t) = 0.

Далее F(¥) =1, так как любой пожар наверняка будет ликвидирован за какой-то конечный промежуток времени. Учитывая, что F(t) - неубывающая функция, аналитически эту функцию во многих случаях можно записать так:

F(t) =

0, если t £ 0 е^-^m^t, если t > 0.

(2.1)

Здесь μ - некоторая постоянная, смысл которой будет выяснен несколько позже. Можно использовать и функцию Ф(t) = 1 – F(t) = P{t_т>t}. Ее аналитическое выражение будет иметь вид

Ф(t) =

0, если t £ 0 е^-^m^t, если t > 0.

(2.2)

Закон распределения, заданный функциям (2.1) или (2.2), играет большую роль в теории вероятностей и ее приложениях (в теории массового обслуживания, теории надежности) и называется показательным (экспоненциальным) законом распределения.

Плотность f(t) показательного закона распределения аналитически записывается так (учитывая, что f(t) = F'(t) = Ф'(t)):

f(t) =

0, если t £ 0 mе^-^m^t, если t > 0.

(2.3)

Используя выражения (2.1) ¸ (2.3), можно определить вероятность того, что продолжительность тушения пожара будет находиться в интервале [t₁, t₂]:

t₂

Р {t₁ £ t_раб < t₂} = F(t₂) – F(t₁) = 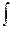f(t)dt = е^-mt1 – е^-mt2 = Ф(t₁) – Ф(t₂). (2.4)

t₁

Выясним физический смысл параметра m показательного закона распределения. Для этого найдем математическое ожидание и дисперсию распределения.

Для определения значения математического ожидания продолжительности пожаротушения М(t_р), если этот процесс описывается показательным законом распределения, нужно вычислить

М(t_р) = 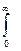tf(t)dt = 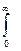tme^-mt dt. (2.5)

Применяя метод интегрирования по частям, находим

М(t_р) = t_ср.р. = 1/m. (2.6)

Отсюда становится ясным физический смысл параметра m - он равен обратной величине среднего времени боевой работы t_раб (вообще параметр показательного распределения равен обратной величине среднего значения случайной величины, распределенной по показательному закону).

Вычисляя аналогичным образом дисперсию случайной величины, подчиняющейся показательному распределению, получаем

D(t_р) = 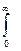t²me^-mtdt - (1/m)² = 1/m². (2.7)

Таким образом,

s(t_р) = 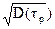= 1/m. (2.8)

Итак, если случайная величина подчиняется показательному закону распределения (2.1), то ее среднее значение равно среднеквадратическому отклонению. Именно поэтому при формировании статистической гипотезы о характере закона распределения некоторой непрерывной и случайной величины М(x) полезно сопоставлять значения s(x).

Если они окажутся достаточно близкими друг к другу, то можно предположить, что данная случайная величина описывается показательным законом распределения и проверить эту гипотезу с помощью критериев согласия. Показательным законом во многих случаях хорошо описываются такие ситуации, когда плотность распределения той или иной временной характеристики сравнительно быстро убывает при возрастании времени t. Это бывает, например, когда подавляющее большинство вызовов обслуживается пожарными подразделениями очень быстро, а длительные задержки в обслуживании вызовов наблюдаются редко. Так, рассматривая достаточно большой промежуток времени общего потока вызовов пожарных подразделений в городе и исследуя время боевой работы, можно предположить, что оно будет подчиняться показательному закону распределения, так как подавляющее большинство выездов связано с ошибочными или ложными вызовами или небольшими загораниями, ликвидация которых занимает очень мало времени. Такое предположение можно высказать (правда, с меньшей степенью уверенности) относительно времени прибытия пожарных подразделений к месту вызова, так как при правильной дислокации пожарных частей первые подразделения должны прибывать к месту вызова весьма быстро, а длительных переездов должно быть очень мало.

Время занятости вряд ли будет в большинстве случаев подчиняться показательному закону, так как с учетом времени следования к месту вызова и обратно оно будет сравнительно мало и характер кривой плотности распределения будет иной. Поэтому не следует думать, что показательный закон распределения временных характеристик процесса пожаротушения будет встречаться очень часто. Во многих случаях эти характеристики лучше будут описываться законом Эрланга (или каким-нибудь другим законом распределения). Закон Эрланга является в некотором смысле обобщением показательного закона распределения. Его плотность имеет следующее аналитическое выражение:

f(t) = [m(mt)^к / k!]е^-mt (t > 0; k = 0,1, …). (2.9)

Очевидно, при к=0 мы имеем показательный закон распределения, который можно иначе называть законом Эрланга нулевого порядка (при k=1 получим соответственно закон Эрланга первого порядка и т.д.).

Используя свойства математических ожиданий и дисперсий, получим, что математическое ожидание случайной величины, подчиненной закону Эрланга k-го порядка (2.9), равно

М(x) = (k + 1) /m. (2.10)

Дисперсия и стандарт (среднее квадратическое отклонение) соответственно равны

D(x) = (k + 1) / m²; (2.11)

k

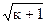s(x) = / m. (2.12)

Вес вышеперечисленные гипотезы о характере распределения тех или иных временных характеристик оперативной деятельности пожарной охраны получили в последние годы достаточно широкую статистическую проверку во многих российских и зарубежных городах.

В большинстве обследованных городов средняя продолжительность занятости пожарных подразделений обслуживанием вызовов не превышает 1ч и обычно составляет 0,8 - 0,9 ч в сутки.

Дата добавления: 2015-07-02