Пример 1. Решить в целых числах уравнение

Пример 1.

Решить в целых числах уравнение

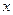
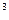
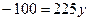
Решение:

Очевидно, что х должен быть кратным пяти. Полагая x = 5z, получаем

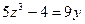(1)

Левая часть этого уравнения должна быть кратная девяти, и т.к. число 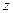может быть представлено в одном из трех видов: 3t, 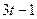, , 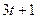то подстановкой этих выражений в уравнение (1) убеждаемся, что число, кратное девяти, дает только тот случай, когда z может быть представлено в виде .

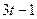В этом случае

,

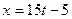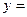
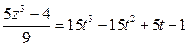
При любом целом 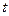получаем соответственно целые решения данного уравнения.

Ответ: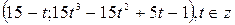

10. Другие методы решения уравнений.

На отдельных примерах рассмотрим несколько частных методов решения уравнений.

При решении следующего уравнения применяется неравенство Коши, справедливое для любых положительных чисел:

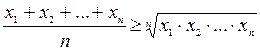
Решить в целых числах уравнение:

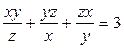
Решение:

1) Заметим, что слагаемые в левой части уравнения имеют одинаковый знак, а поскольку их сумма положительна, то каждое слагаемое также положительно. Поэтому к сумме, стоящей слева, применим неравенство Коши, получим:

3 =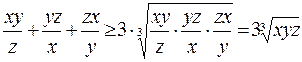

Откуда, .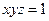

2) Исследуем возможные наборы трех целых чисел, которые в произведении дают 1. Это могут быть тройки (1,1,1), (1,-1,-1), (-1,-1,1), (-1,1,-1).

Непосредственной проверкой убеждаемся, что каждая из них является решением исходного уравнения.

Ответ: (1,1,1), (1,-1,-1), (-1,-1,1), (-1,1,-1).

Замечание: Если относительно одного из неизвестных уравнение является квадратным, то ограничивать перебор можно, используя неотрицательность дискриминанта.

Пример 2.

Решить уравнение в целых числах

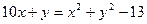
Решение:

Относительно х это уравнение – квадратное: 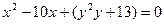. условием существования решения является 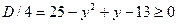, т.е. -3 .

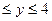Таким образом, достаточно перебрать случаи 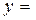4, 3, 2, 1, 0, -1, -2, -3.

Ответ: (-5, -3), (5, 4)

Дата добавления: 2015-07-02