
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пример 5
|
|
|
|
Пример 3.
Сколько целочисленных решений имеет уравнение 
Решение:
После возведения в квадрат получим 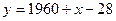
 , тогда
, тогда 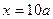
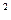 (
(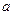 – целое) и
– целое) и 
Таким образом, получаем 15 решений при 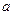 = 0, …, 14.
= 0, …, 14.
Ответ: 15 решений.
Пример 4.
Найти целочисленные решения уравнения 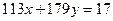 , удовлетворяющие неравенствам
, удовлетворяющие неравенствам 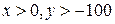
Решение:
Воспользуемся методом, сходным с алгоритмом Евклида.
Имеем 179 = 113 + 66.
Перепишем наше уравнение в виде 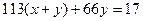
Обозначим 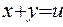 ,
, 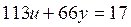 . Как видим, у нового уравнения один из коэффициентов уменьшился. Можно вновь 113 разделить на 66 с остатком, а лучше так:
. Как видим, у нового уравнения один из коэффициентов уменьшился. Можно вновь 113 разделить на 66 с остатком, а лучше так: 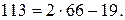
Получаем 
Обозначим 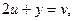

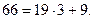
Получаем уравнение
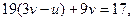
 .
.
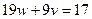 ,
,
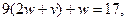

Наконец, получаем уравнение  . Это уравнение имеет очевидное решение:
. Это уравнение имеет очевидное решение:  , где
, где 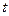 – любое целое число.
– любое целое число.
Двинулись в обратный путь:
 ,
,
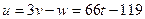 ,
,
 ,
,
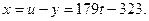
Таким образом, 
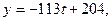 где
где 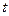 – произвольное целое. Из условия
– произвольное целое. Из условия 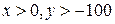 найдем
найдем 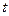 = 2,
= 2, 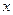 = 35,
= 35, 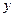 = -22
= -22
Ответ: 
Решить в целых положительных числах уравнение
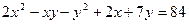
Решение:
Решая данное уравнение как квадратное относительно у, находим:
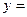
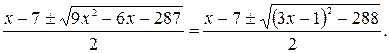 (1)
(1)
Мы видим, что число  должно быть точным квадратом, т.е.
должно быть точным квадратом, т.е.  = u
= u 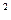
Так как х - натуральное число, то 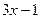 тоже натуральное, число u (как арифметическое значение корня) тоже натуральное, причем, очевидно,
тоже натуральное, число u (как арифметическое значение корня) тоже натуральное, причем, очевидно, 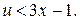
Положим, 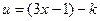 , где
, где 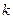 – натуральное число.
– натуральное число.
Тогда получаем: (3х – 1) 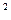 -288 = [(3x – 1) – k]
-288 = [(3x – 1) – k] 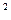 или 2k(3x – 1) = k
или 2k(3x – 1) = k 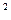 + 288
+ 288
откуда видно, что 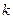 - число четное.
- число четное.
Пусть  (
(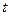 также натуральное число).
также натуральное число).
Тогда находим: 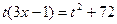
или 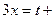
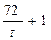 (2)
(2)
Отсюда ясно, что число  должно быть целым, т.е.
должно быть целым, т.е. 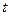 должно быть делителем числа 72. Возможные значения для
должно быть делителем числа 72. Возможные значения для 
Из них надо взять лишь такие, для которых число 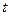 +
+ 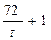 кратно трем (либо это число должно быть равно 3
кратно трем (либо это число должно быть равно 3 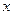 ). Этому условию удовлетворяют лишь числа
). Этому условию удовлетворяют лишь числа 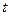
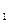 = 2,
= 2, 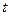
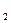 = 8,
= 8, 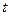
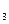 = 9,
= 9, 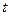
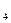 = 36.
= 36.
Подставляя эти значения в (2), находим для 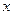 два значения: 13 и 6. Из уравнения (1) найдем соответствующие (только натуральные!) значения
два значения: 13 и 6. Из уравнения (1) найдем соответствующие (только натуральные!) значения 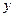 . В результате мы получаем два решения исходной системы:
. В результате мы получаем два решения исходной системы:
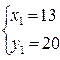

Ответ: 
|
|
|
|
|
Дата добавления: 2015-07-02; Просмотров: 324; Нарушение авторских прав?; Мы поможем в написании вашей работы!