Условие задачи № 4

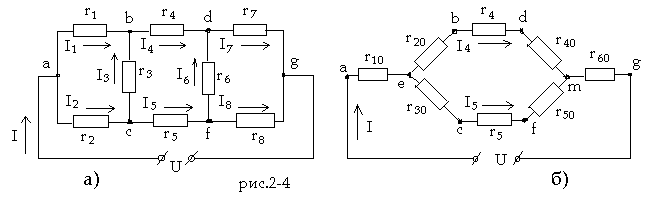
Найти эквивалентное сопротивление цепи (рис.2-4,а) и все токи, если U = 114 B,

r₁ = 30 ом, r₂ = r₃ = 10 ом, r₄ = 26 ом, r₅ = 11 ом, r₆ = 10 ом, r₇ = 40 ом, r₈ = 50 ом.

Решение задачи.

Заменим треугольники сопротивлений abc и dfg эквивалентными звездами (рис.2-4,б). В преобразованной схеме появились новые узлы e и m. Обратим внимание на то, что в преобразованной схеме сохраняются значения токов I, I₄, I₅ в участках цепи, которые не подвергались преобразованию.

Подсчитаем сопротивления лучей звезды r₁₀, r₂₀, r₃₀, эквивалентной треугольнику abc сопротивлений r₁, r₂, r₃.

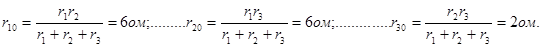
Определим сопротивления лучей звезды r₄₀, r₅₀, r₆₀, эквивалентной треугольнику dfg сопротивлений r₆, r₇, r₈:

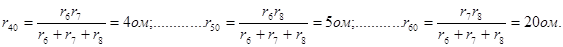
Входное сопротивление всей схемы

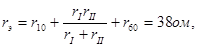где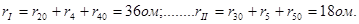

Ток в неразветвленной части цепи

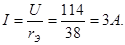
Токи в параллельных ветвях:

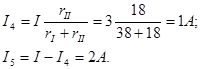
Теперь найдем токи в сопротивлениях заданной цепи. Для этого предварительно из схемы рис 2-4,б определим напряжения между точками a и b, a и с, с и b, d и g, f и g,

f и d:

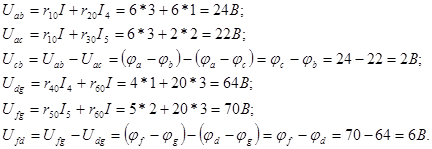
Искомые токи:

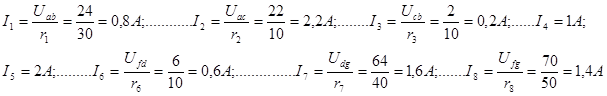
2.3 МЕТОД УЗЛОВЫХ ПОТЕНЦИАЛОВ

Условие задачи № 5.

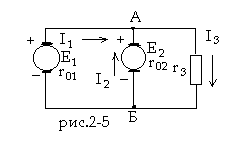
Два параллельно включенных генератора (рис.2-5) с э.д.с. E₁ = E₂ = 230 B и внутренними сопротивлениями r₀₁ = 0,5 ом и r₀₂ = 0,4 ом питают потребитель, эквивалентное сопротивление которого r₃ = 10 ом. Определить все токи, мощности генераторов, мощности потерь на внутренних сопротивлениях, а также мощность потребителя r₃.

Решение задачи.

Применим метод двух узлов (частный случай метода узловых потенциалов). Этот метод пригоден для расчета цепей, имеющих только два узла (при любом числе ветвей).

Для расчета применяется формула, определяющая напряжение между узловыми точками:

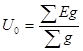
где -- алгебраическая сумма произведений э.д.с. на проводимость ветви;

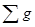-- сумма проводимостей ветвей.

Так, для рассматриваемой цепи (рис.2-5)

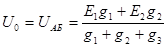
Здесь в числителе отсутствует слагаемое 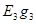, так как э.д.с. в третьей ветви нет. Если бы, например, э.д.с. E₂ действовала в обратном направлении, то перед слагаемым 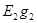надо было бы поставить знак минус.

Определяем проводимости ветвей:

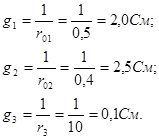
Узловое напряжение

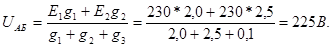
Рассматриваемая цепь (рис.2-5) имеет три ветви с токами I₁, I₂, I₃, направления которых до расчета цепи неизвестны, поэтому надо выбрать произвольно их положительные направления (стрелки на рис.2-5)

Принятые направления токов совпадают с направлениями действия э.д.с.. В таком случае узловое напряжение, или напряжение на концах ветви с э.д.с.., равно разности э.д.с. источника и падения напряжения на сопротивлении ветви, т.е.

откуда

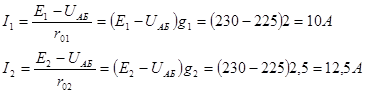
По закону Ома ток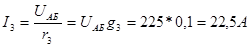

Мощности, развиваемые источниками:

P₁ = E₁I₁ = 230*10 = 2,30 кВт; P₂ = E₂I₂ = 230*12,5 = 2,875 кВт.

Мощности потерь на внутренних сопротивлениях:

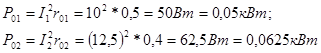
Мощность потребителя

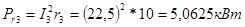
Составим баланс мощностей:

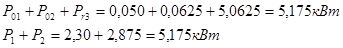
Итак, 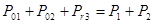, значит расчет выполнен правильно.

Условие задачи № 6.

Для схемы рис.2-6, а) пользуясь методом узловых потенциалов, определить все токи. Дано: E₁ = 30 B, E₂ = 10 B, E₃ = 200 B, E₄ = 56 B, r₁ = 20 ом, r₂ = 30 ом, r₃ = 6 ом, r₄ = 8 ом, r₅ = 15 ом, r₆ = 40 ом и r₇ = 10 ом.

Решение задачи.

Примем потенциал точки 3 равным нулю 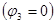. Запишем систему уравнений для определения потенциалов точек 1 и 2:

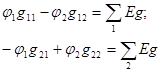(6-1)

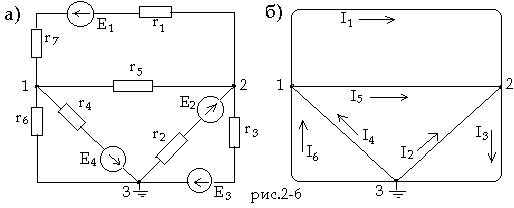
Подсчитаем g₁₁ – сумму проводимостей ветвей, присоединенных к узлу 1:

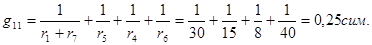
Аналогично g₂₂ – сумма проводимостей ветвей, присоединенных к узлу 2:

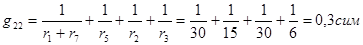
Сумма проводимостей, соединяющих первый и второй узлы,

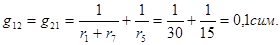
Подставляя числовые значения в уравнения (6-1), получим:

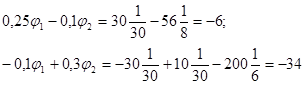
Решим последние два уравнения, найдем потенциалы точек 1 и 2:

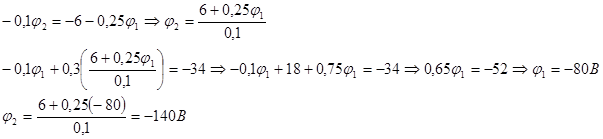Наконец, применяя закон Ома для отдельных ветвей, определим искомые токи: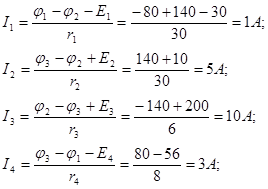

Направления найденных токов указаны на структурной схеме рис.2-6,б) цепи

рис.2-6,а).

Условие задачи № 7

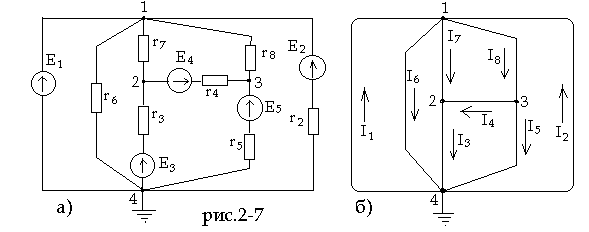
Методом узловых потенциалов определить токи во всех ветвях схемы, изображенной на рис.2-7а). Заданы: E₁ = 20 B, E₂ = 30 B, E₃ = 2 B, E₄ = 1,2 B, E₅ = 5,6 B, r₂ = 50 ом,

r₃ = 10 ом, r₄ = 20 ом, r₅ = 10 ом, r₆ = 100 ом, r₇ = 50 ом, r₈ = 20 ом.

Решение задачи.

Методом узловых потенциалов рекомендуется пользоваться в тех случаях, когда при этом методе число уравнений будет меньше числа уравнений, составленных по методу контурных токов.

Если в схеме некоторые узлы соединяются источниками напряжения (их сопротивления равны нулю), то число Y уравнений, составляемых по методу узловых потенциалов, уменьшается:

Y = N_у -- N_н – 1, (7-1)

где N_у – число узлов; N_н – число ветвей, содержащих только источники напряжения.

В нашем случае в цепи имеется ветвь с источником напряжения, не содержащая сопротивления. Целесообразно принять равным нулю потенциал одной из узловых точек, к которой подходит указанная ветвь, например потенциал узла 4 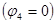. Тогда потенциал точки 1 имеет значение, равное E₁, т.е. 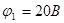. Общее число уравнений, согласно формуле (7-1), равно двум (N_у = 4, N_н = 1, Y = N_у – N_н – 1 = 2). Таким образом, в данной задаче достаточно составить по методу узловых потенциалов всего два уравнения для узлов 2 и 3:

для узла 2

,

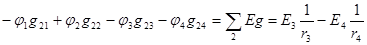для узла 3

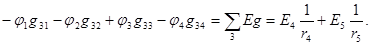
Найдем проводимости ветвей. Проводимости g₂₄ и g₃₄ искать нет необходимости, так как их произведения с 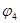даст нулевой результат.

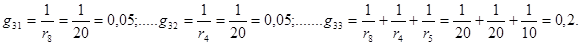
Подставим в уравнения числовые значения проводимостей, э.д.с., а также значения 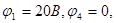получим следующую систему уравнений:

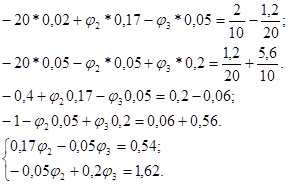
Решая эту систему уравнений, найдем:

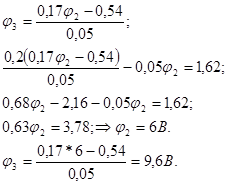
Наконец, применяя к отдельным ветвям формулы закона Ома, получим значения всех токов, которые нанесены на структурной схеме(рис.2-7,б):

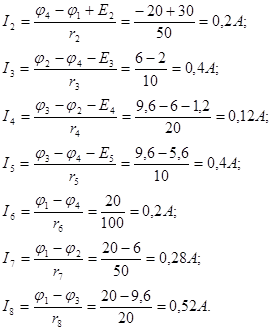
Обращаем особое внимание на то, что в ветви без сопротивления ток I₁ не определяется законом Ома и вычисляется на основании первого закона Кирхгофа:

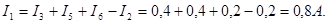
2.4 МЕТОД КОНТУРНЫХ ТОКОВ

Условие задачи № 8.

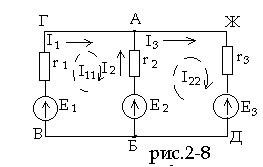Для цепи рис.2-8 дано: E₁ = 60 B; E₂ = 48 B;

E₃ = 6 B; r₁ = 200 ом; r₂ = 100 ом; r₃ = 10 ом.

Определить се токи методом контурных токов.

Решение задачи.

Метод контурных токов основан на использовании только второго закона Кирхгофа, что позволяет уменьшить число уравнений, которые надо решать совместно.

Достигается это разделением схемы на ячейки (независимые контуры) и введением для каждой ячейки (контура) своего тока – контурного тока, являющегося расчетной величиной.

Так, в заданной цепи (рис.2-8) можно рассмотреть две ячейки (ГАБВГ и АЖДБА) и ввести для них контурные токи: соответственно I₁₁ и I₂₂.

Из схемы цепи ясно, что для внешних ветвей (ГВ и ЖД) контурные токи совпадают с токами ветвей, т.е. I₁ = I₁₁ и I₃ = I₂₂. Для внутренней ветви схемы (ветвь АБ) ток I₂ определяется разностью контурных токов, т.е. I₂ = I₂₂ – I₁₁ (здесь учтено, что ток I₂ направлен согласно току I₂₂ и встречно току I₁₁).

Таким образом, в рассматриваемой цепи два контурных тока позволяют выразить токи трех ветвей.

Следующая операция – это определение собственных и общих сопротивлений контуров. Сумма всех сопротивлений контура называется его собственным сопротивлением и для контура ГАБВГ составляет

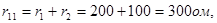для контура АЖДБА собственное сопротивление

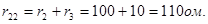
Сопротивление общей ветви двух контуров (ветвь АБ) называется их общим сопротивлением. Оно обозначается для первого контура r₁₂, для второго r₂₁. Поскольку r₁₂ и r₂₁ составляют сопротивление одной и той же ветви, то, очевидно, что r₁₂ = r₂₁. В нашем случае

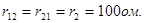
Составим контурное уравнение (уравнение по второму закону Кирхгофа) для контура БВГАБ:

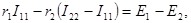
или, объединив все члены уравнения с токами I₁₁ и I₂₂, получим:

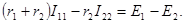
В этом уравнении алгебраическая сумма падений напряжений выражается произведением тока рассматриваемого контура I₁₁ на его собственное сопротивление r₁₁ и произведением тока другого контура I₂₂ на общее сопротивление первого и второго контуров r₁₂, т.е.

Аналогично составим уравнение для контура АЖДБА:

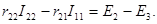
Подставив значения сопротивлений и э.д.с., получим:

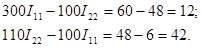
Таким образом, вычисление контурных токов I₁₁ и I₂₂ сводится к решению системы двух уравнений.

Умножив второе уравнение на 3 и сложив его почленно с первым, получим:

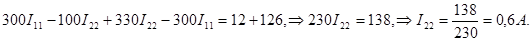
Подставляя значение I₂₂ в первое контурное уравнение, находим:

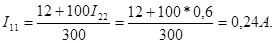
Используя записанные выше соотношения между токами контуров и ветвей, получаем значения токов ветвей:

I₁ = 0,24 A; I₃ = 0,6 A; I₂ = I₂₂ – I₁₁ = 0,6 – 0,24 = 0,36 A.

Условие задачи № 9.

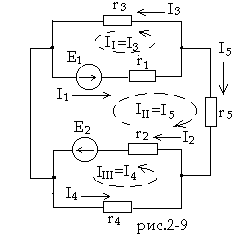Найти токи всех ветвей цепи схемы (рис.2-9), пользуясь методом контурных токов, если э.д.с.

E₁ = E₂ = 30 B и сопротивления r₁ = r₂ = 1 ом, r₃ = 4 ом,

r₄ = 2 ом, r₅ = 3 ом. Составить баланс мощностей.

Решение задачи.

Допустим, что токи I₃, I₄ и I₅ внешних ветвей цепи рис.2-9 являются контурными токами, замыкающимися, как указано на схеме пунктиром,

I_I = I₃, I_II = I₅, I_III = I₄. В смежных ветвях с сопротивлениями r₁ и r₂ этой схемы проходят по два контурных тока, поэтому токи таких ветвей определяются алгебраическим суммированием соответствующих контурных токов.

Составим систему уравнений контурных токов:

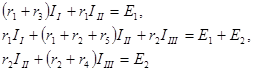
Подставляя числовые значения сопротивлений и э.д.с., а затем решая полученную систему уравнений, найдем значения контурных токов:

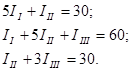
Выразим ток I₂ из первого уравнения и подставим найденное значение в другие уравнения:

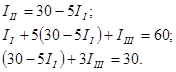
Раскроем скобки и приведем подобные члены:

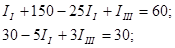
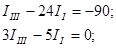
Выразим из последнего уравнения ток I_III и подставим значение в оставшееся уравнение:

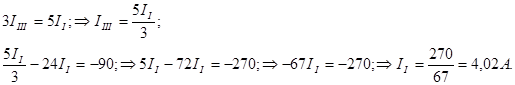
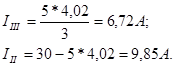
Токи ветвей будут:

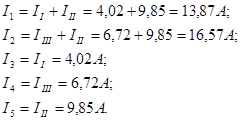
Составляем баланс мощностей. Мощности источников питания:

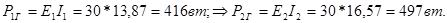
Мощности приемников энергии:

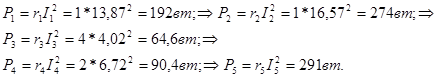
Баланс мощностей:

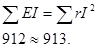
Условие задачи № 10.

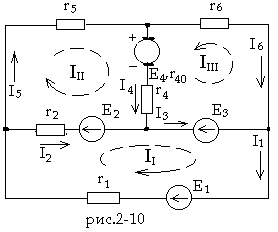Методом контурных токов найти токи в цепи, схема которой изображена на рис.2-10. Даны:

E₁ = 100B, E₂ = 30B, E₃ = 10B, E₄ = 6B,

r₁ = 10 ом, r₂ = 10 ом, r₄ = 6 ом, r₅ = 5 ом,

r₆ = 15 ом, r₄₀ = 1 ом.

Решение задачи.

Выберем направления контурных токов, которые обозначим через I_I, I_II, I_III.

Составим систему уравнений для контуров:

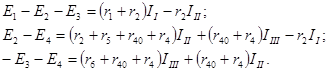
После подстановки числовых значений имеем:

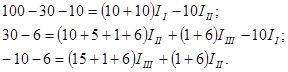
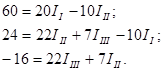
Выражаем из первого уравнения ток I_II, при этом сокращая его на 10:

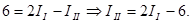
Подставим это значение в два оставшихся уравнения:

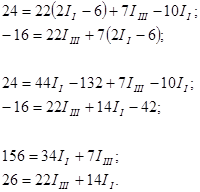
Выразим из первого уравнения I_III и подставим это значение во второе уравнение, найдем значение тока I_I:

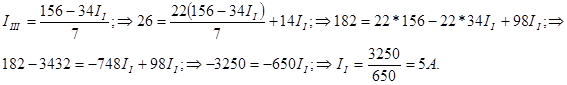
Далее найдем другие контурные токи:

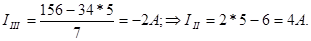
С помощью найденных контурных токов найдем истинные токи во всех ветвях.

В ветви, где действует э.д.с. E₁, истинный ток I₁ имеет направление контурного тока I_I и равен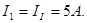

В ветви с сопротивлением r₅ истинный ток I₅ имеет направление контурного тока I_II и равен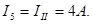

В ветви с сопротивлением r₆ истинный ток I₆ имеет направление, противоположное контурному току I_III, и равен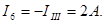

В ветви с сопротивлением r₂ истинный ток I₂ получится от наложения контурных токов I_I и I_II и будет иметь направление большего контурного тока I_I:

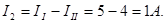
В ветви с сопротивлением r₄ истинный ток I₄ получится от наложения контурных токов I_II и I_III и будет иметь направление контурного тока I_II:

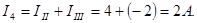
В ветви, где действует э.д.с. E₃, истинный ток I₃ получится от наложения контурных токов I_I и I_III и будет иметь направление тока I_I:

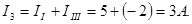
Покажем, как эта же задача может быть решена с помощью определителей. Для этого уравнения контурных токов следует записать в форме (смотри раздел 1.5):

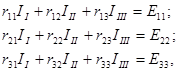
где

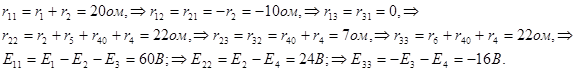
Составим определитель 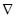и вычислим его значение:

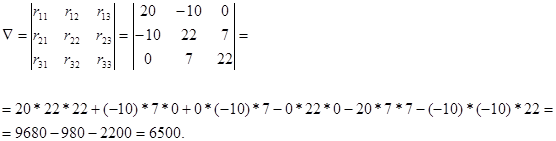
Вычислим значения алгебраических дополнений определителя, рассчитав его миноры и умножив каждый из них на (-1)^k+j, где k – номер вычеркиваемой строки, а j – номер вычеркиваемого столбца; 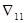- это алгебраическое дополнение, получающееся из основного определителя 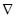путем вычеркивания первой строки и первого столбца, умноженное на (-1)¹⁺¹:

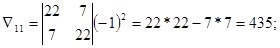
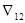- алгебраическое дополнение, получающееся из основного определителя при вычеркивании первой строки и второго столбца, умноженное на (-1)¹⁺²:

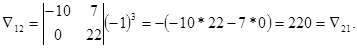
Аналогично найдем:

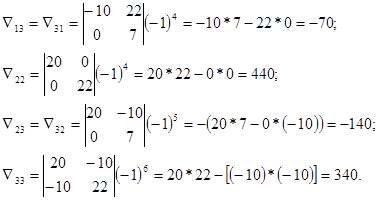
По формуле (5-1) (смотри раздел 1-5) находим контурные токи:

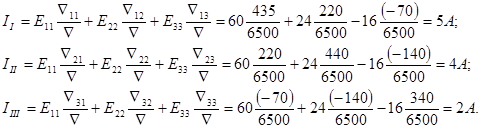
Таким образом, получили те же результаты, что и ранее. Дальнейшее нахождение истинных токов в ветвях описано выше.

2.5 МЕТОД НАЛОЖЕНИЯ

Условие задачи № 11.

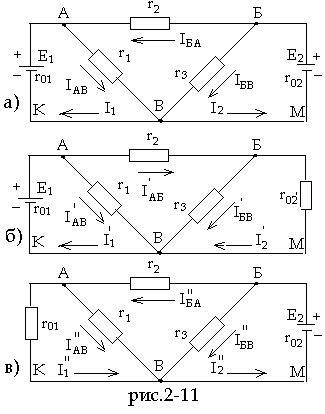
Для цепи рис.2-11 определить токи во всех участках и напряжения между узловыми точками А, Б и В при следующих данных:

r₁ = r₃ = 2 ом; r₂ = 1,6 ом; E₁ = 3,6 B; E₂ = 4,8 B; r₀₁ = r₀₂ = 0,5 ом.

Решение задачи.

По методу наложения ток в любом участке цепи рассматривается как алгебраическая сумма частичных токов, созданных каждой э.д.с. в отдельности. В нашем случае следует: во-первых, определить частичные токи от э.д.с. E₁ при отсутствии э.д.с. E₂, т.е. рассчитать простую цепь по рис.2-11б); во-вторых, найти частичные токи от э.д.с. E₂ при отсутствии э.д.с. E₁, т.е. рассчитать простую цепь по рис.2-11в); в-третьих, алгебраически сложить частичные токи двух последних схем.

Итак, метод наложения позволяет заменить расчет одной сложной цепи с несколькими источниками энергии (рис.2-11а) расчетом нескольких (в данном случае двух) цепей с одним источником энергии в каждой.

Все частичные токи в нашей задаче от э.д.с. E₁ (рис.2-11б) обозначим буквой I с одним штрихом, а все частичные токи от э.д.с. E₂ (рис.2-11в) – с двумя штрихами. Для цепи с э.д.с. E₁ (рис.2-11б) рассчитаем сначала общее сопротивление. Сопротивление участка БВ

Оно соединено последовательно с сопротивлением r₂, поэтому

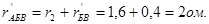
Два одинаковых сопротивления 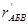и r₁ соединены параллельно, поэтому общее сопротивление всей внешней цепи

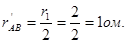
Ток источника 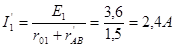разветвляется в узловой точке А на два одинаковых тока:

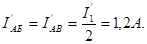
Ток 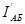разветвляется в узловой точке Б на токи:

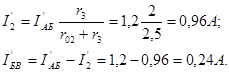
Для цепи с э.д.с. E₂ (рис.2-11в)

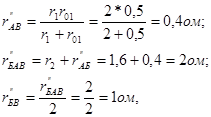
так как 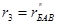. В ветви источника с э.д.с. E₂ ток

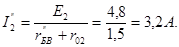
Поскольку 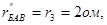то ток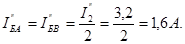

Токи в параллельных ветвях участка АВ

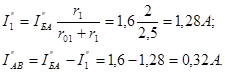
Выполним алгебраическое сложение частичных токов. На участке ВКА частичный ток 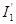(рис.2-11б) направлен от узла В к узлу А, а частичный ток 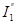(рис.2-11в) – от А к В, т.е. навстречу первому. Поэтому суммарный ток

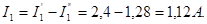
Направление тока I₁ (рис.2-11а) совпадает с направлением большего частичного тока, т.е. тока .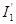

Аналогичным образом определяем I_БА и I₂:

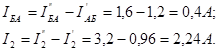
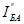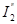Направления токов I_БА и I₂ (рис.2-11а) совпадают с направлениями токов и соответственно.

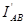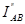В ветви АВ оба частичных тока ( и ) совпадают по направлению, поэтому

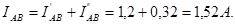
Аналогично

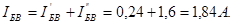
Вычислим напряжения между узловыми точками

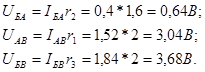
Для проверки расчетов составим уравнения по законам Кирхгофа.

Для узла А: 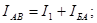действительно, 1,52 = 1,12 + 0,4.

Для узла Б: 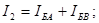действительно, 2,24 = 0,4 + 1,84.

Для контура АБВ: 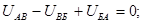действительно, + 3,04 – 3,68 + 0,64 = 0 (обход против направления движения стрелки часов).

Условие задачи № 12.

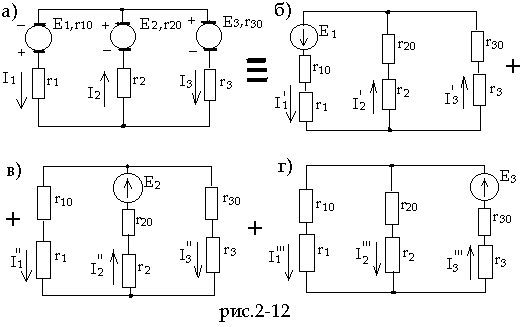
Методом наложения рассчитать токи в схеме рис.2-12а), если E₁ = 10 B, E₂ = 40 B,

E₃ = 5 B, r₁₀ = 5 ом, r₂₀ = r₃₀ = 2 ом, r₁ = 30 ом, r₂ = 3 ом, r₃ = 8 ом.

Решение задачи.

Обозначим положительные направления токов исходной схемы на рис.2-12а). Предположим, что действует только э.д.с. E₁, а э.д.с. E₂ и E₃ – недействующие (рис.2-12б).

Тогда

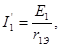
где

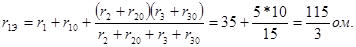
Ток

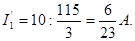
Токи в параллельных ветвях определяются по формуле:

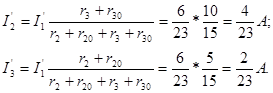
Проведем расчет, предполагая, что действует э.д.с. E₂, а э.д.с. E₁ и E₃ не действуют (рис.2-12в):

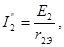
где

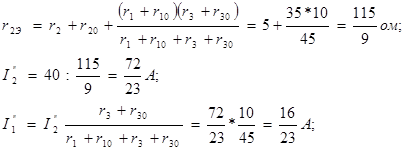
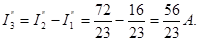
Аналогично рассчитаем величины токов при действии только одной э.д.с. E₃ (рис.2-12г):

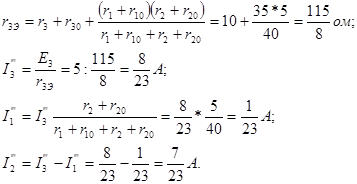
Истинное значение тока в каждой ветви найдется как алгебраическая сумма токов, определяемых действием каждой э.д.с. в отдельности.

Ток в первой ветви

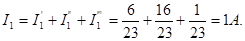
Ток во второй ветви

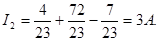
Ток в третьей ветви

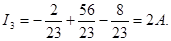
2.6 МЕТОД ЭКВИВАЛЕНТНОГО ГЕНЕРАТОРА.

Условие задачи № 13.

Для схемы рис.2-13а) методом эквивалентного генератора напряжения найти ток в ветви с сопротивлением r₁, если E₁ = 18 B, E₂ = 21 B, r₁₀ = 1 ом, r₁ = 2 ом, r₂₀ = 2 ом,

r₂ = 7 ом, r₃ = 6 ом.

Решение задачи.

Обозначим положительное направление искомого тока I₁ на исходной схеме (см. рис.2-13а). Рассмотрим часть схемы, подключенную к исследуемой первой ветви (обведенную штриховой линией), в качестве эквивалентного генератора напряжения с э.д.с. E_г и сопротивлением r_г. Нарисуем эквивалентную электрическую схему с эквивалентным генератором напряжения (рис.2-13б).

На схеме произвольно выбрано положительное направление э.д.с. эквивалентного генератора E_г к точке p. Это позволяет записать для режима холостого хода эквивалетного генератора с отключенной первой ветвью (рис.2-13в)

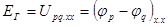
Развернутая схема эквивалентного генератора в режиме холостого хода показана на рис.2-13г). Во внутренних ветвях генератора ток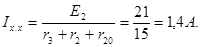

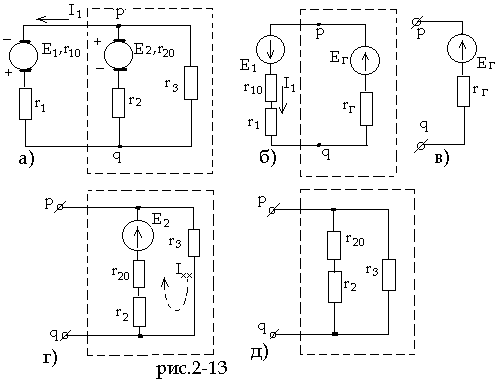
Напряжение холостого хода определяет э.д.с. генератора:

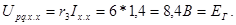
Найдем сопротивление 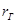эквивалентного генератора.

Для подсчета сопротивления генератора преобразуем его схему (см.рис.2-13г), заменив источник напряжения E₂ короткозамкнутым участком (рис.2-13д). Входное сопротивление последней схемы является сопротивлением эквивалентного генератора

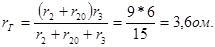
Возвращаясь к схеме рис.2-13б, находим искомый ток по закону Ома:

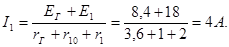
Условие задачи № 14.

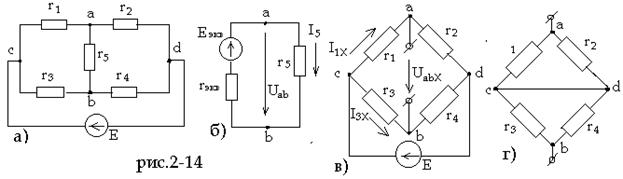
Определить ток в измерительной диагонали неуравновешенного моста (рис.2-14а), воспользовавшись методом эквивалентного генератора, если E = 6 B, r₁ = r₂ = 1 ком,

r₃ = 4 ком, r₄ = 2 ком и r₅ = 2,17 ком.

Решение задачи.2

В соответствии с теоремой об эквивалентном генераторе воздействие всей цепи на рассматриваемую ветвь с сопротивлением r₅ можно заменить воздействием эквивалентного генератора (рис.2-14б), э.д.с. E_экв и внутреннее сопротивление r_экв которого равны

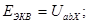
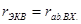
Для определения напряжения U_{ab X} разомкнем ветвь с сопротивлением r₅ (рис.2-14в):

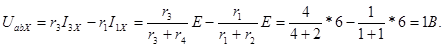
Сопротивление r_экв определяем по схеме рис.2-14г):

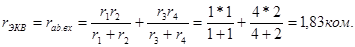
Ток диагонали находим из схемы рис.2-14б)

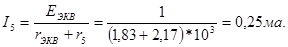
Дата добавления: 2015-07-02