КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вектор скорости точки
|
|
|
|
Векторный способ задания движения точки.
Векторный, 2) координатный, 3) естественный (или траекторный).
Способы задания движения точки
Для задания движения точки можно применять один из следующих трех способов:
Пусть точка 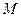 движется по отношению к некоторой системе отсчета
движется по отношению к некоторой системе отсчета 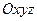 (рис.1.1). Положение этой точки в любой момент времени можно определить,
(рис.1.1). Положение этой точки в любой момент времени можно определить,

Рисунок 1.1
задав её радиус-вектор 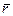 , проведенный из начала координат в точку
, проведенный из начала координат в точку 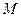 . При движении точки
. При движении точки 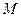 вектор
вектор 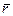 будет с течением времени изменяться и по модулю, и по направлению. Следовательно,
будет с течением времени изменяться и по модулю, и по направлению. Следовательно, 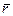 является переменным вектором (вектором-функцией), зависящим от аргумента
является переменным вектором (вектором-функцией), зависящим от аргумента  :
:
 . .
| (1) |
Это равенство и определяет закон движения точки в векторной форме, так как оно позволяет в любой момент времени построить соответствующий вектор 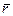 и найти положение движущейся точки.
и найти положение движущейся точки.
Геометрическое место концов вектора 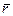 , т.е. годограф этого вектора, определяет траекторию движущейся точки.
, т.е. годограф этого вектора, определяет траекторию движущейся точки.
Аналитически, как известно, вектор задается его проекциями на координатные оси. Для вектора 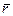 будет:
будет:
 и
и 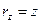 ,
,
где  - координаты точки. Тогда, если ввести единичные векторы (орты) координатных осей, получим для вектора выражение
- координаты точки. Тогда, если ввести единичные векторы (орты) координатных осей, получим для вектора выражение
 . .
| (2) |
Следовательно, зависимость  будет известна, если будут заданы координаты
будет известна, если будут заданы координаты  точки как функции времени. Такой способ задания движения точки (координатный) рассмотрим ниже.
точки как функции времени. Такой способ задания движения точки (координатный) рассмотрим ниже.
2.Координатный способ задания движения точки.
Чтобы знать закон движения точки, т.е. её положение в пространстве в любой момент времени, надо знать значения координат точки для каждого момента времени, т.е. знать зависимости
|
Эти уравнения и есть уравнения движения точки в прямоугольных декартовых координатах. Они определяют закон движения точки при координатном способе задания движения.
Если движение происходит в одной и той же плоскости, то, приняв эту плоскость за плоскость Oxy, получим
|
При прямолинейном движении точки, если вдоль ее траектории направить координатную ось Ох, движение будет определяться одним уравнением

| (5) |
Это и есть закон прямолинейного движения.
3. Естественный способ задания движения точки.
Естественным (или траекторным) способом задания движения удобно пользоваться, когда траектория точки известна заранее. Пусть кривая 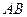 является траекторией точки
является траекторией точки 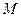 при её движении относительно координат
при её движении относительно координат 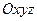 (рис. 1.2). Выберем на этой траектории точку (неподвижную) О и примем её за начало отсчета, и установим на траектории положительное и отрицательное направление отсчета. Положение точки
(рис. 1.2). Выберем на этой траектории точку (неподвижную) О и примем её за начало отсчета, и установим на траектории положительное и отрицательное направление отсчета. Положение точки 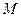 на траектории будет однозначно определяться криволинейной координатой
на траектории будет однозначно определяться криволинейной координатой  , которая равна расстоянию от точки О до точки
, которая равна расстоянию от точки О до точки 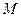 , измеренному вдоль дуги траектории и взятому с соответствующим знаком. При перемещении точки расстояние S с течением времени будет изменяться.
, измеренному вдоль дуги траектории и взятому с соответствующим знаком. При перемещении точки расстояние S с течением времени будет изменяться.

Рисунок 1.2
Чтобы знать положение точки 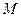 на траектории в любой момент времени надо знать зависимость
на траектории в любой момент времени надо знать зависимость
 . .
| (6) |
Это уравнение и выражает закон движения точки 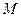 вдоль траектории.
вдоль траектории.
Таким образом, чтобы задать движение точки естественным способом, надо задать: 1) траекторию точки; 2) начало отсчета на траектории с указанием знака (+ или –); 3) закон движения точки вдоль траектории в виде  .
.
Одной из кинематических характеристик движения точки является векторная величина, называемая скоростью точки.
Скорость точки - это векторная величина, характеризующая быстроту и направление движения точки в данной системе отсчета.
Введем сначала понятие о средней скорости точки за какой-нибудь промежуток времени. Пусть движущаяся точка находится в момент времени  в положении
в положении 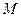 (рис. 1.3), определяемом радиус-вектором
(рис. 1.3), определяемом радиус-вектором 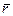 , а в момент
, а в момент 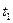 приходит в положение
приходит в положение  , определяемое вектором
, определяемое вектором 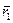 . Тогда перемещение точки за промежуток времени
. Тогда перемещение точки за промежуток времени  определяется вектором
определяется вектором 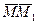 , который будем называть вектором перемещения точки. Этот вектор направлен по хорде, если точка движется криволинейно (рис. 1.3,а), и вдоль самой траектории
, который будем называть вектором перемещения точки. Этот вектор направлен по хорде, если точка движется криволинейно (рис. 1.3,а), и вдоль самой траектории 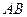 , когда движение является прямолинейным (рис. 1.3,б).
, когда движение является прямолинейным (рис. 1.3,б).

Рисунок 1.3
Из треугольника  , видно, что
, видно, что 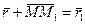 , следовательно,
, следовательно,
 .
.
Отношение вектора перемещения точки к соответствующему промежутку времени дает векторную величину, называемую средней по модулю и направлению скоростью точки за промежуток времени 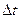 :
:
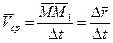 . .
| (7) |
Направлен вектор 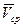 так же, как и вектор
так же, как и вектор 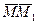 , т.е. при криволинейном движении вдоль хорды
, т.е. при криволинейном движении вдоль хорды 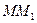 , в сторону движения точки, а при прямолинейном движении – вдоль самой траектории.
, в сторону движения точки, а при прямолинейном движении – вдоль самой траектории.
Очевидно, что чем меньше промежуток времени 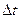 , тем величина
, тем величина 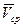 будет точнее характеризовать движение точки.
будет точнее характеризовать движение точки.
Поэтому скоростью точки 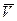 в данный момент времени
в данный момент времени  называется векторная величина
называется векторная величина 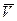 , к которой стремится скорость
, к которой стремится скорость 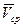 при стремлении промежутка времени
при стремлении промежутка времени 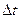 к нулю.
к нулю.
 .
.
Предел отношения 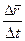 при
при  представляет собой первую производную от вектора
представляет собой первую производную от вектора 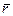 по аргументу
по аргументу  и обозначается
и обозначается  , тогда
, тогда
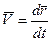 . .
| (8) |
Итак, вектор скорости точки в данный момент времени равен первой производной от радиус-вектора точки по времени. Так как предельным направлением секущей 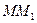 является касательная, то вектор скорости в данный момент времени направлен по касательной к траектории точки в сторону движения.
является касательная, то вектор скорости в данный момент времени направлен по касательной к траектории точки в сторону движения.
Размерность скорости  , т.е.
, т.е. 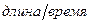 . Единицы измерения
. Единицы измерения 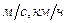 .
.
|
|
|
|
|
Дата добавления: 2015-06-27; Просмотров: 1913; Нарушение авторских прав?; Мы поможем в написании вашей работы!

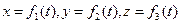 .
.