
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Скорость точки
|
|
|
|
Скорость и ускорение точки при естественном способе задания движения
При естественном способе задания движения точки заданы траектория точки и закон движения точки вдоль этой траектории в виде S=f(t).
В этом случае значения 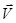 и
и 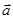 определяют по их проекциям не на оси системы отсчета Oxyz, а на подвижные оси Mτnb, имеющие начало в точке М и движущиеся вместе с нею(рис.1.7). Эти оси называют осями естественного трехгранника (или скоростными осями) и направлены они следующим образом:
определяют по их проекциям не на оси системы отсчета Oxyz, а на подвижные оси Mτnb, имеющие начало в точке М и движущиеся вместе с нею(рис.1.7). Эти оси называют осями естественного трехгранника (или скоростными осями) и направлены они следующим образом:
ось Мτ – по касательной к траектории в сторону положительного отсчета расстояния S;
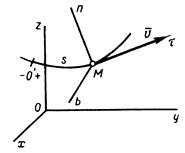
Рисунок 1.7
ось Mn – по нормали к траектории, лежащей в соприкасающейся плоскости и направленной в сторону вогнутости траектории;
ось Mb – перпендикулярно к первым двум так, чтобы она образовала с ними правую систему осей.
Mn – называется главной нормалью, если она лежит в соприкасающейся плоскости (в плоскости самой кривой, если кривая плоская), перпендикулярная ей нормаль Mb – бинормалью.
Найдем значение скорости точки 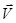 . Если за промежуток времени
. Если за промежуток времени 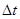 точка совершит вдоль дуги траектории перемещение
точка совершит вдоль дуги траектории перемещение 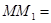 Δ S (рис. 1.2), где одновременно Δ S – приращение координаты S, то численно средней скоростью точки за этот промежуток времени будет
Δ S (рис. 1.2), где одновременно Δ S – приращение координаты S, то численно средней скоростью точки за этот промежуток времени будет 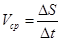 и в пределе, найдем, что
и в пределе, найдем, что
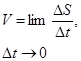 или или 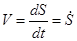 . .
| (16) |
Таким образом, числовое значение скорости точки в данный момент времени равно первой производной от расстояния (криволинейной координаты) S этой точки по времени.
Значение скорости V можно также находить как отношение элементарного перемещения dS точки к соответствующему промежутку времени dt. Так как всегда dt> 0, то знак скорости совпадает со знаком dS. Следовательно, когда V> 0, скорость направлена в сторону положительного отсчета расстояния S, а когда V <0, - в противоположную сторону. Таким образом, величина V одновременно определяет и модуль скорости, и сторону, куда она направлена.
|
|
|
|
|
Дата добавления: 2015-06-27; Просмотров: 377; Нарушение авторских прав?; Мы поможем в написании вашей работы!