Скорости и ускорения точек тела

Рассмотрим скорости и ускорения точек тела, движущегося вокруг неподвижной точки. Так как при этом движении в каждый момент времени тело имеет мгновенную ось вращения ОР, вокруг которой происходит поворот с угловой скоростью 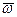(рис. 4.5), то

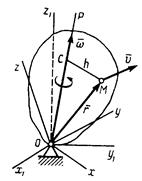
Рисунок 4.5

вектор скорости какой-нибудь точки М тела будет определяться равенством

,

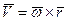(60)

где 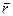- радиус-вектор, проведенный в точку М из неподвижной точки О. Направлен вектор 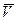перпендикулярно плоскости МОР, проходящей через точку М и ось ОР в сторону поворота тела, т.е. куда указывает стрелка 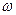. Численно

,

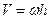(61)

где h=MC – расстояние точки М до мгновенной оси вращения тела ОР, вдоль которой направлен вектор .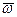

Геометрически скорость любой точки М тела в данный момент времени можно найти, зная в этот момент скорость 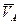какой-нибудь точки А тела и направление скорости 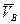другой точки В этого тела. Пусть 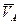и направление 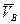известны. Проведем тогда через точку А плоскость 1, перпендикулярную вектору 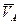. Как показано (рис. 4.6), мгновенная ось ОР должна лежать в этой плоскости. Но одновременно ось ОР должна лежать в плоскости 2, проведенной через точку В перпендикулярно вектору 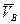. Следовательно, прямая, по которой пересекутся эти плоскости, и будет мгновенной осью вращения ОР. Теперь, определив расстояние h точки А от оси ОР, по формуле 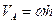найдем угловую скорость тела в данный момент вре-

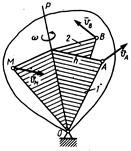
Рисунок 4.6

мени: 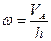. После этого значение скорости 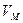любой точки М тела находится по формуле 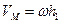, а вектор 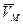будет направлен перпендикулярно плоскости ОМР.

В частном случае, когда известно, что скорость какой-то точки тела равна в данный момент времени нулю, прямая, проходящая через эту точку и неподвижную точку О тела, будет мгновенной осью вращения и расчет существенно сократится.

Аналитически скорость 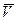определяется по ее проекциям на какие-нибудь координатные оси. Найдем проекции вектора 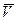на оси Oxyz, жестко связанные с телом и движущиеся с ним (см. рис. 4.4); эти оси имеют то преимущество, что в них координаты x, y, z точки М будут величинами постоянными. Так как 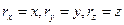, то

= .

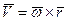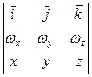Отсюда, разлагая определитель по элементам первой строки и учитывая, что 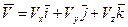и что, следовательно, коэффициенты при 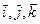в этом разложении должны равняться 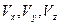соответственно, получим

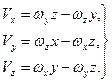
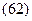
Эти формулы, как и формула (60), называют формулами Эйлера.

В частном случае формулы (62), конечно справедливы и при вращательном движении тела вокруг неподвижной оси z. Так как при этом 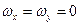и 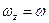, то для такого случая

.

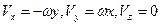Вектор ускорения точки М определим как производную вектора скорости по времени, т.е. дифференцируя по времени равенство 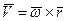; в результате чего получим 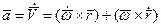. Так как 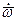= 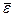, а 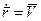, то окончательно

.

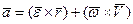(63)

Первое слагаемое этого равенства называют вращательной составляющей ускорения, обозначим её 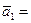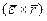. Вектор 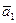направлен перпендикулярно плоскости, проходящей через точку М и вектор 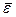(рис. 4.7), в ту сторону, куда указывает дуговая стрелка ,

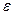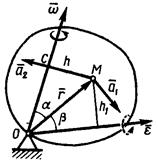
Рисунок 4.7

а по модулю

,

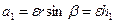где 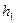- расстояние от точки М до вектора .

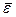Второе слагаемое 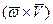называют осестремительной составляющей ускорения, обозначим её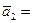 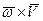. Вектор 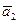направлен как вектор векторного произведения векторов 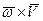(т.е. перпендикулярно одновременно двум векторам 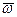– и , и 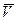), что дает направление вдоль МС, т.е. по перпендикуляру, опущенному из точки М на мгновенную ось вращения ОР, вдоль которой направлен вектор 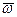. По модулю 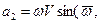^ 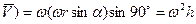, так как .

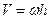Заметим, что в отличие от результатов, полученных для вращающегося тела, здесь (при сферическом движении тела) 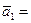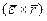не будет вектором касательного ускорения точки М (по касательной направлен вектор 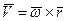, а направление вектора 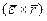будет вообще другим); следовательно, и вектор 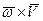не будет вектором нормального ускорения точки М.

Таким образом, формула (63) примет вид

.

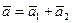Это равенство выражает теорему Ривальса об ускорении точки тела, совершающего сферическое движение: ускорение точки тела, вращающегося вокруг неподвижной точки, равно векторной сумме вращательного и осестремительного ускорений.

В общем случае вращательное и осестремительное ускорения не перпендикулярны друг другу, следовательно, модуль ускорения точки, как диагонали параллелограмма ускорений, вычисляют по формуле

.

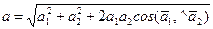Дата добавления: 2015-06-27