Сложение поступательных движений

Теорема о сложении ускорений (теорема Кориолиса)

Найдем зависимость между относительным, переносным и абсолютным ускорениями точки.

Абсолютное ускорение точки в сложном движении определим, продифференцировав 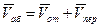по времени, т.е.

.

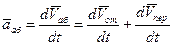(70)

Следует обратить внимание на то, что при абсолютном движении изменение каждого из векторов слагается из изменений при относительном и переносном движениях. Учитывая это можно записать

,

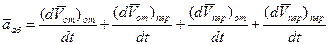(71)

где в индексе после скобок указан тот вид движения, при совершении которого изменяется вектор, стоящий внутри скобок.

Но по определению относительное ускорение характеризует изменение относительной скорости только при относительном движении; движение осей Oxyz, т.е. переносное движение при этом во внимание не принимается. Поэтому

.

(72)

В свою очередь, переносное ускорение характеризует изменение переносной скорости только при переносном движении, поэтому

.

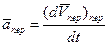(73)

Другие два слагаемых правой части равенства образуют так называемое кориолисово ускорение точки

.

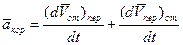(74)

Величина , характеризующая изменение относительной скорости точки при переносном движении и изменение переносной скорости точки при её относительном движении, называется поворотным, или кориолисовым, ускорением точки.

Таким образом, получаем

.

(75)

Это равенство выражает теорему о сложении ускорений (теорема Кориолиса): при сложном движении ускорение точки равно геометрической сумме относительного, переносного и поворотного, или кориолисова ускорений.

Найдем для вычисления формулу, вытекающую из равенства (74).

Начнем с определения 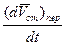. При рассматриваемом переносном движении вектор , направленный по касательной кривой АВ, переместится вместе с этой кривой поступательно (придет в положение 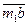, рис. 5.3) и одновременно повернется вокруг точки

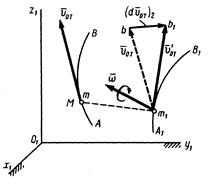
Рисунок 5.3

до положения 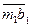. В результате вектор получит в переносном движении приращени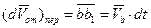е , где 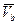- скорость, с которой перемещается точка b при повороте вектора 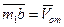вокруг точки . Так как этот поворот происходит с угловой скоростью 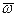, то по формуле . В результате получаем 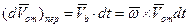и

.

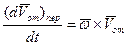(76)

Теперь определим . Скорость равна скорости той неизменно связанной с подвижными осями точки m кривой АВ, с которой в данный момент времени совпадает точка М (рис. 5.4). Если точку О принять за полюс и обозначить через вектор 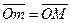, то .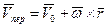

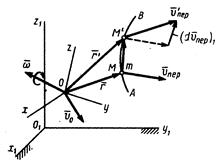
Рисунок 5.4

Совершив за промежуток времени dt относительное перемещение , точка придет в положение , для которого и

.

Следовательно, вследствие того, что точка совершает относительное перемещение , вектор получает приращение ,

откуда

.

(77)

Тогда согласно (74) получим

.

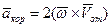(78)

Таким образом, кориолисово ускорение равно удвоенному произведению переносной угловой скорости (угловой скорости подвижной системы отсчета) на относительную скорость точки.

Модуль кориолисова ускорения, если угол между векторам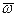и и обозначить через α, будет равен

.

(79)

Направлен вектор так же, как и вектор 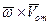, т.е. перпендикулярно плоскости, проходящей через векторы 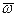и , в ту сторону, откуда кратчайшее совмещение 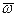с видно происходящим против хода часовой стрелки (рис. 5.5).

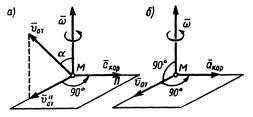
Рисунок 5.5

Глава 13. Сложное движение тела

13.1. Сложение поступательных движений.

13.2. Сложение вращений вокруг двух параллельных осей.

13.3. Цилиндрические зубчатые передачи.

13.4. Сложение вращений вокруг пересекающихся осей.

13.5. Сложение поступательного и вращательного движений. Винтовое движение.

Рассмотрим случай, когда относительное движение тела является поступательным со скоростью , а переносное движение тоже поступательное со скоростью . Тогда все точки тела в относительном движении будут иметь скорость , а в переносном - . По теореме сложения скоростей все точки тела в абсолютном движении имеют одну и ту же скорость , т.е. абсолютное движение тоже будет поступательным.

Итак, при сложении двух поступательных движений со скоростями и результирующее движение также будет поступательным со скоростью .

Дата добавления: 2015-06-27