Сложение поступательного и вращательного движений. Винтовое движение

Рассмотрим тело, вращающееся с угловой скоростью 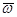вокруг оси, жестко скрепленной с другим телом, имеющим поступательное движение со скоростью (рис. 6.6). В зависимости от значения угла α между векторам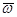и и здесь возможны три случая.

Рисунок 6.6

1. Скорость поступательного движения перпендикулярна оси вращения ( ). Пусть сложное движение тела слагается из вращательного движения вокруг оси Аа с угловой скоростью 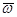и поступательного движения со скоростью , перпендикулярной 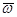(рис. 6.7). Легко видеть, что это плоскопараллельное движение. Тогда движение слагается из поступательного со скоростью (если точку А считать полюсом) и вращательного вокруг оси Аа, проходящей через полюс.

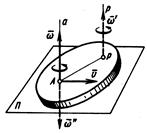
Рисунок 6.7

Вектор можно заменить парой угловых скоростей , беря их соответственно 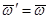, а 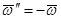. При этом расстояние АР определится из равенства , откуда (учитывая, что )

.

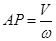(85)

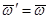Векторы при сложении дают нуль, и мы получаем, что движение тела в этом случае можно рассматривать как мгновенное вращение вокруг оси с угловой скоростью , то есть точка Р является мгновенным центром скоростей. Здесь мы еще раз убеждаемся, что поворот тела вокруг осей Аа и происходит с одной и той же угловой скоростью 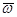, т.е. вращательная часть движения не зависит от выбора полюса.

2. Винтовое движение ().

Ось Аа называют осью винта (рис. 6.8). Когда векторы и 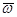направлены в разные стороны, то при принятом нами правиле изображения 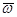винт будет левым, если в одну сторону, - правым.

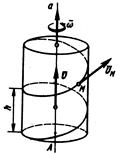
Рисунок 6.8

Расстояние, проходимое за время одного оборота любой точкой, лежащей на оси винта, называется шагом h винта. Если величины 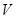и 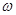постоянны, то шаг винта также будет постоянным. Обозначая время одного оборота через Т, получаем в этом случае и 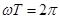, откуда .

При постоянном шаге любая точка М тела, не лежащая на оси вала, описывает винтовую линию.

Скорость произвольной точки М слагается из переносной скорости поступательного движения 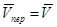, и перпендикулярной ей относительной скорости , получаемой во вращательном движении и равной 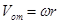, следовательно

.

3. Скорость поступательного движения образует произвольный угол с осью вращения. Сложное движение, совершаемое телом в этом случае, представляет собой общий

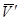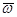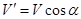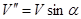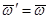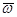случай движения свободного тела. Разложим вектор (рис. 6.9,а) на составляющие , направленную вдоль (), и , перпендикулярную (). Скорость можно заменить парой угловых скоростей и , после чего векторы и 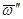можно отбросить. Расстояние АС найдем по формуле (78)

.

Тогда у тела остается вращение с угловой скоростью 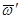и поступательное движе-

Рисунок 6.9

ние со скоростью 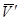. Следовательно, распределение скоростей точек тела в данный момент времени будет таким же, как и при винтовом движении вокруг оси Сс с угловой скоростью 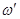= 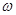и поступательной скоростью .

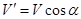Проделанными операциями (рис. 6.9,б) мы перешли от полюса А к полюсу С. Результат подтверждает, что в общем случае движения твердого тела угловая скорость при переносе полюса не изменяется 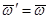, а меняется только поступательная скорость.

Так как при движении свободного твердого тела величины , 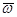и α будут все время изменяться, то будет непрерывно изменяться и положение оси Сс которую называют мгновенной винтовой осью. Таким образом, движение свободного тела можно еще рассматривать как слагающееся из серии мгновенных винтовых движений вокруг непрерывно изменяющихся винтовых осей.

Дата добавления: 2015-06-27