КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Общий случай движения свободного твердого тела
|
|
|
|
Рассмотрим наиболее общий случай движения твердого тела, когда оно является свободным и может перемещаться как угодно по отношению к системе отсчета 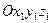 (рис. 4.8).
(рис. 4.8).
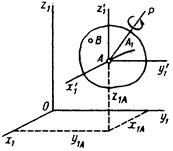
Рисунок 4.8
Установим вид уравнений, определяющих закон рассматриваемого движения. Выберем произвольную точку А тела в качестве полюса и проведем через неё оси 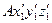 , которые при движении тела будут перемешаться вместе с полюсом поступательно. Тогда положение тела в системе отсчета
, которые при движении тела будут перемешаться вместе с полюсом поступательно. Тогда положение тела в системе отсчета 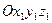 будет известно, если будем знать положение полюса А, т.е. его координаты
будет известно, если будем знать положение полюса А, т.е. его координаты  , и положение тела по отношению к осям
, и положение тела по отношению к осям 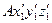 , определяемое, как и в случае рассмотрения движения тела, имеющего одну неподвижную точку, т.е. определяемую углами Эйлера φ;ψ;θ (рис.4.1). Следовательно, уравнения движения свободного твердого тела, позволяющие найти его положение по отношению к системе отсчета
, определяемое, как и в случае рассмотрения движения тела, имеющего одну неподвижную точку, т.е. определяемую углами Эйлера φ;ψ;θ (рис.4.1). Следовательно, уравнения движения свободного твердого тела, позволяющие найти его положение по отношению к системе отсчета 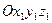 в любой момент времени, имеют вид
в любой момент времени, имеют вид
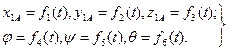
| (64) |
Первые три из уравнений определяют поступательную часть движения вместе с полюсом А. Последние три уравнения определяют сферическое движение тела вокруг точки А, которое, как было установлено, представляет собой последовательность элементарных поворотов вокруг мгновенных осей вращения. Отсюда сделаем вывод, что в общем случае движение свободного твердого тела можно рассматривать как слагающееся из поступательного движения, при котором все точки тела движутся как произвольно выбранный полюс А со скоростью 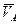 , и из серии элементарных поворотов с угловой скоростью
, и из серии элементарных поворотов с угловой скоростью 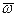 вокруг мгновенных осей вращения, проходящих через полюс А (рис. 4.9).
вокруг мгновенных осей вращения, проходящих через полюс А (рис. 4.9).
Соответственно этому основными характеристиками движения являются: скорость 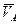 и ускорение
и ускорение 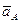 полюса А, а также угловая скорость
полюса А, а также угловая скорость 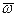 и угловое ускорение
и угловое ускорение 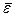 вращения тела вокруг полюса. Если в качестве полюса принять другую точку тела, например, какую-нибудь
вращения тела вокруг полюса. Если в качестве полюса принять другую точку тела, например, какую-нибудь
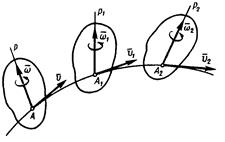
Рисунок 4.9
точку В (рис. 4.8), то величины 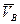 и
и 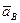 в общем случае не будут равны
в общем случае не будут равны 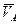 и
и 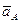 , а величины
, а величины 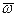 и
и 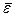 останутся неизменными (как и для плоскопараллельного движения тела, эти величины от выбора полюса не зависят).
останутся неизменными (как и для плоскопараллельного движения тела, эти величины от выбора полюса не зависят).
Скорость любой точки М в рассматриваемом движении слагается из скорости 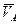 полюса А и скорости
полюса А и скорости 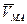 , которую точка М получает при сферическом движении тела вокруг полюса А. Скорость
, которую точка М получает при сферическом движении тела вокруг полюса А. Скорость
 . .
| (65) |
Таким образом,
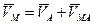 или или 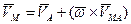 . .
| (66) |
Аналогично для ускорения любой точки М найдем
|
или
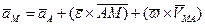 .
.
Глава 12. Сложное движение точки
12.1. Относительное, переносное и абсолютное движения.
12.2. Теорема о сложении скоростей.
12.3. Теорема о сложении ускорений (теорема Кориолиса).
|
|
|
|
|
Дата добавления: 2015-06-27; Просмотров: 564; Нарушение авторских прав?; Мы поможем в написании вашей работы!