Движение твердого тела, имеющего одну неподвижную точку

Рассмотрим движение твердого тела, одна из точек которого во все время движения остается неподвижной. При таком движении тела все другие его точки движутся по сферическим поверхностям, центры которых совпадают с неподвижной точкой. По этой причине движение тела вокруг неподвижной точки называют ещё сферическим движением тела.

Примером сферического движения твердого тела может служить движение волчка, имеющего неподвижную точку.

Рассмотрим движение твердого тела по отношению к неподвижной системе отсчета 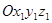, у которой точка О совпадает с неподвижной точкой О тела (рис. 4.1). Положение тела по отношению к этой системе отсчета можно определить следующим образом. С

Рисунок 4.1

движущимся телом жестко скрепим систему осей Oxyz. Теперь для определения положения тела следует задать положение подвижной системы осей Oxyz по отношению к неподвижной системе отсчета 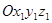. Для этой цели Эйлер предложил использовать три угловые координаты: угол собственного вращения, угол прецессии, угол нутации.

Прямая ОК, вдоль которой пересекаются плоскости Oxy и , называется линией узлов. Тогда положение тела по отношению к осям 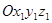можно определить по положению трехгранника Oxyz, а сними и самого тела можно определить углами (углами Эйлера):

(51)

Тогда φ – угол собственного вращения; ψ – угол прецессии; θ – угол нутации. Положительные направления отсчета углов показаны на рис. 4.1 дуговыми стрелками.

Углы Эйлера являются независимыми параметрами (координатами), характеризующими положение тела с одной неподвижной точкой. Чтобы знать положение тела в любой момент времени, надо знать зависимости

.

(52)

Эти уравнения, определяющие закон происходящего движения, называются уравнениями движения тела вокруг неподвижной точки.

Произвольное движение тела, при котором изменяются величины углов φ,ψ,θ, представляется как совокупность трех движений: 1) вращение вокруг оси Oz (собственное вращение) с угловой скоростью ; 2) вращение вокруг оси (прецессия) с угловой скоростью ; 3) вращение вокруг линии узлов ОК (нутация) с угловой скоростью 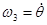. Векторы 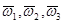этих угловых скоростей направлены соответственно по осям Oz, и ОК (рис. 4.2).

Рисунок 4.2

Поскольку при движении тела изменяются все три угла, движение тела представляет собой вращение с угловой скоростью 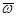, равной геометрической сумме названных угловых скоростей. Таким образом,

;

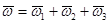ось этого вращения ОР, вдоль которой направлен вектор 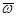, при движении меняет свое направление в пространстве, но проходит все время через неподвижную точку О. По этой причине 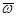называют мгновенной угловой скоростью, а ось ОР – мгновенной осью вращения.

Процесс движения тела вокруг неподвижной точки можно представить как последовательность элементарных поворотов вокруг мгновенных осей вращения.

Мгновенная ось представляет собой геометрическое место точек тела, скорости которых в данный момент времени равны нулю.

Для определения вектора 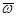найдем его проекции на подвижные оси Oxyz (рис. 4.3). Вектор 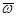можно представить в виде

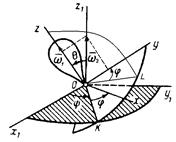
Рисунок 4.3

,

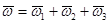(53)

где численно

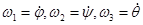
(54)

Проектируя обе части равенства (53) на оси x, y, z, получим:

, , .

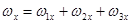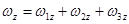(55)

Проекции векторов и находим сразу [см. рис. 4.3 и обозначения (54)]:

, ; , , .

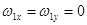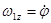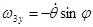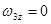Для определения проекций вектора проведем через оси и 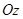плоскость, которая пересечется с плоскостью вдоль линии OL. так как линия ОК перпендикулярна плоскости 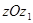, то она перпендикулярна и линии OL ( 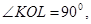а . Тогда, проектируя вектор на линию OL, а эту проекцию в свою очередь на оси Ох и Oy, получим:

, , .

Подставляя все вычисленные проекции в правые части равенств (55), найдем окончательно

(56)

Уравнения (56) называются кинематическими уравнениями Эйлера. Они определяют проекции вектора угловой скорости тела 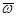на подвижные оси через углы Эйлера; тем самым определяется и вектор .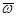

Аналогично можно найти проекции вектора 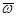на неподвижные оси 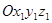. Соответствующие формулы имеют вид

(57)

При сферическом движении тела положение мгновенной оси вращения со временем изменяется, а, следовательно, изменяется не только модуль, но и направление вектора угловой скорости.

Изменение вектора 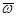характеризуется векторной величиной

,

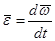(58)

называемой угловым ускорением тела в данный момент времени или мгновенным ускорением.

При изменении вектора 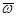его конец А будет описывать в пространстве некоторую кривую AD, являющуюся годографом вектора 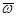(рис. 4.4). Тогда сравнивая выражение углового ускорения 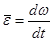с равенством 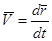, приходим к выводу, что ускорение

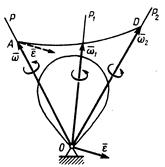
Рисунок 4.4

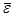можно вычислить как скорость, с которой конец вектора 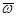перемещается вдоль кривой AD. В частности, направление 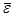совпадает с направлением касательной к кривой AD в соответствующей точке. Следовательно, в данном случае, в отличие от случая вращения вокруг неподвижной оси, направление вектора 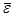не совпадает с направлением вектора .

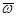Векторы 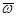и 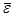являются основными кинематическими характеристиками движения тела, имеющего неподвижную точку. Их можно определить аналитически, зная уравнения движения (52).

Значения 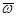можно найти и геометрически.

Используя равенства (57), можно определить проекции на неподвижные оси 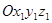вектора 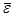. Так как значение 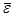дается формулой (58), то

.

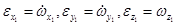(59)

Эти проекции и определяют вектор 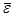. Таким образом, зная уравнения движения (52), можно по полученным формулам найт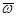и и .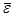

Дата добавления: 2015-06-27