Общие теоремы при ударе

Теорема об изменении количества движения следует из (7.7)

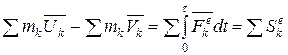. (11.3)

Здесь слева стоит разность количеств движения системы после и до удара, справа – геометрическая сумма внешних ударных импульсов. От внутренних ударов количество движения системы не зависит.

Разновидностью (11.3) является теорема об изменении движения центра масс

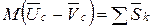, (11.4)

где 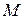- масса системы, 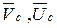- скорость центра масс до и после удара.

Теорема об изменении кинетического момента выводится из равенства:

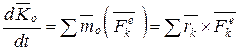, (11.5)

где – кинетический момент системы относительно неподвижного центра, 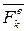- внешние силы, 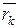- радиусы-векторы точек приложения сил.

Проинтегрируем обе части равенства (11.5) по времени

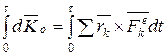
(11.6)

где 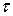- время удара. Величины 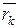при ударе остаются постоянными, а потому из (11.6) следует теорема:

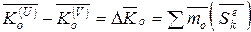
(11.7)

Изменение кинетического момента системы относительно некоторого центра за время удара равно сумме моментов внешних ударных импульсов относительно того же центра. От внутренних ударов кинетический момент не зависит.

Заметим еще, если правую часть в (11.3), (11.4) или (11.6) обратить в нуль, то придем к соответствующим законам сохранения, утверждающим: когда внешняя мера воздействия на систему равна нулю, мера движения системы остается неизменной.

Что касается закона изменения кинетической энергии при ударе, то он выражается теоремами Карно. При этом под ударом понимается либо мгновенное наложение на систему связей, либо мгновенное освобождение системы от связей.

1. Случай мгновенного наложения абсолютно неупругих идеальных связей. Таковыми называют связи, которые, будучи наложенными при ударе, продолжают действовать и после удара. Теорема Карно утверждает (первая теорема):

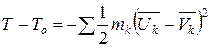
(11.8)

где 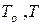- кинетическая энергия до и после удара, - скорости точек до и после удара, разности 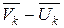называют потерянными скоростями. Очевидно, при мгновенном наложении на систему абсолютно неупругих идеальных связей происходит потеря кинетической энергии, равной кинетической энергии, соответствующей потерянным скоростям.

2. Случай мгновенного снятия абсолютно неупругих идеальных связей. Таковыми называют связи, которые, будучи снятыми при ударе, отсутствуют и после удара. Теорема Карно (вторая теорема) утверждает:

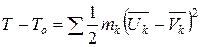
(11.9)

где разности 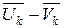называют приобретенными скоростями. Правая часть положительна, что свидетельствует об увеличении энергии: кинетическая энергия, приобретенная системой в результате мгновенного снятия связей, равна кинетической энергии, соответствующей приобретенным скоростям.

3. Общая теорема Карно:

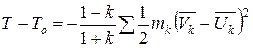
(11.10)

При мгновенном наложении на систему упругих связей возникают потери кинетической энергии, и величина этих потерь зависит не только от потерянных скоростей, но и от коэффициента восстановления.

Дата добавления: 2015-06-27