Малые свободные колебания системы с двумя степенями свободы

Пусть дана система с двумя степенями свободы и - обобщенные координаты. Кинетическая и потенциальная энергия системы дается формулами (10.2):

Функции Т и П определенно положительны, а потому:

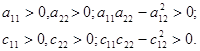
(10.11)

Уравнения Лагранжа для соответствующих координат:

(10.12)

(9.46)

Подставив (10.2) в (10.12), получим дифференциальные уравнения малых колебаний системы с двумя степенями свободы:

(10.13)

Примем решение системы в виде:

,

(10.14)

где A, B, k, α – некоторые постоянные. Подставив (10.14) в (10.13), и сократив на 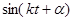, получим:

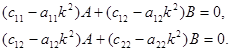
(10.15)

Система имеет нулевое решение A=B=0, соответствующее устойчивому положению равновесия. Для ненулевых решений составим из (10.15) отношение:

.

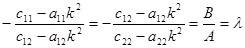(10.16)

Из первого равенства находим:

.

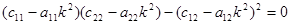(10.17)

Данное условие, служащее для определения частот, называют уравнением частот. Запишем его в виде:

(10.18)

где ; .

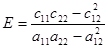Квадратное (относительно ) уравнение (10.18) в силу неравенств устойчивости имеет два вещественных положительных корня. Расположим их в порядке возрастания:

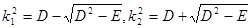
(10.19)

Отсюда найдем две частоты. Одна из них 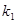- низшая, другая - высшая. Это собственные частоты системы. Колебание с частотой 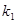называют первым главным колебанием, с частотой - вторым главным колебанием системы.

Вернувшись к решению (10.14), мы можем теперь записать – для первого главного колебания:

(10.20)

Для второго главного колебания:

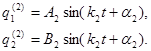
(10.21)

Главные колебания являются колебаниями гармоническими.

Подставив поочередно 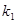и в (10.16), найдем связи между амплитудами A и B в главных колебаниях: . Множител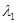и и называют коэффициентами собственных форм (коэффициентами распределения амплитуд). Они могут быть как положительными, так и отрицательными. При обе координаты в главном колебании находятся в одной фазе; при - в противофазе.

Результирующее движение по каждой координате будет суммой двух главных колебаний:

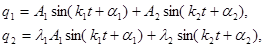
(10.22)

где 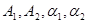- зависят от начальных условий, 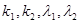- от начальных условий не зависят и определяются параметрами самой колебательной системы. В общем случае частоты 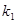и несоизмеримы, а потому результирующее движение не будет периодическим.

Примеры.

1. Определить собственные частоты и собственные формы колебаний (малых) двойного математического маятника, образованного двумя материальными точками равной массы m и двумя стержнями длиной каждый.

Подобная система в общем виде была рассмотрена в примере 2 (§34). Воспользуемся полученными там формулами (2) и (3).

При , получим:

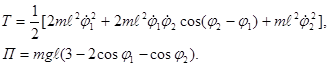
(1)

Функции T и П должны быть приведены к квадратичным формам:

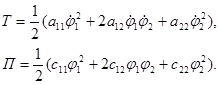
(2)

Так как колебания малые, то с точностью до малых второго порядка включительно:

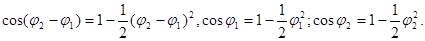
(3)

С учетом (3) из (1), замечаем:

(4)

Сравнивая (4) и (2), замечаем:

Раскрывая уравнение (7.52) частот, получим:

Из (9.50) находим коэффициенты распределения: .

Первое главное колебание:

Движение в фазе - в каждое мгновение стержни вращаются в одном направлении.

Второе главное колебание:

Движение в противофазе – в каждое мгновение стержни вращаются в прямо противоположных направлениях.

Формы колебаний показаны на рис. 50. Во втором главном колебании имеется особенная точка F, которая остается неподвижной. Такие точки называют узлами. Концевая точка O к узлам не относится.

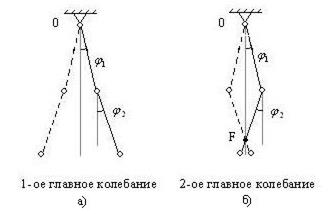
Рис. 50

2. Два твердых тела с массам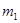и и 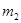и две пружины, жесткостью 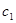и 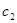, объединены в систему, которая располагается на гладкой горизонтальной плоскости и может совершать малые прямолинейные колебания.

Определить собственные частоты и установить формы колебаний.

Рис. 51

Пусть - обобщенные координаты, отсчитываемые от положений равновесия тел. Кинетическая и потенциальная энергия:

Для упрощения выкладок возьмем упрощенный вариант: .

В результате:

.

Коэффициенты квадратичных форм:

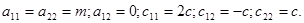
Уравнение для вычисления частот:

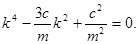
Его решение:

По формулам (9.50) находим:

Картина движения показана на рис. 52. При втором главном колебании точка F остается неподвижной (узел).

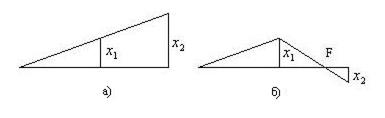
Рис. 52

Первое главное колебание:

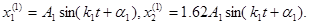
Тела движутся в фазе, либо вправо либо влево. Амплитуда колебаний второго тела в 1,62 раза больше.

Второе главное колебание:

Тела движутся в противофазе: либо навстречу друг другу, к узлу, либо расходятся от узла. Амплитуда колебаний второго тела составляет 0,62 амплитуды первого.

Дата добавления: 2015-06-27