Малые свободные колебания системы с одной степенью свободы

Для системы с одной степенью свободы уравнения Лагранжа при малых колебаниях:

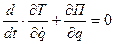
Кинетическая и потенциальная энергия:

.

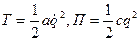Выполняя над Т и П указанные действия, получим:

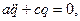
(10.5)

или

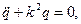
(10.6)

где 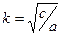- угловая частота колебаний, 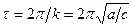- период.

Общее решение уравнения (10.6) можно принять в одной из таких форм:

,

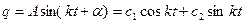(10.7)

,

где 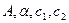- произвольные постоянные, определяемые по начальным условиям; А – амплитуда, α – начальная фаза. Приняв во внимание разложение функции 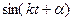, нетрудно установить связь между одной и другой парой постоянных:

.

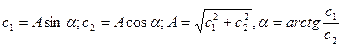(10.8)

Остановимся на первом представлении и найдем постоянные A и α. Положим, что в начальный момент времени t = 0 задано:

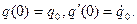
(10.9)

Исходим из того, что

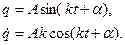
Сюда подставим t = 0 и (10.9):

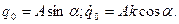
Решая данную систему, найдем:

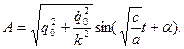
(10.10)

Замечание. Если в задаче требуется определить лишь частоту или период малых колебаний, то нет необходимости в составлении и решении дифференциального уравнения колебаний. В этом случае достаточно составить кинетическую и потенциальную энергию в форме 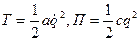, и затем найти то, что требуется:

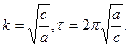
Пример.

Однородный цилиндр радиуса R и массы M может кататься без скольжения по горизонтальной плоскости. В точках и цилиндра шарнирно прикреплены пружины длиной 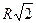и жесткостью каждая. Другие концы пружин закреплены на плоскости катания. Когда диаметр AB горизонтален (положение равновесия), пружины не напряжены. Определить период малых колебаний цилиндра.

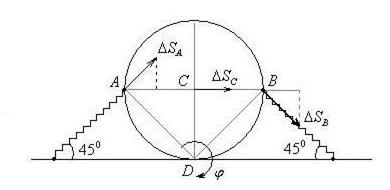
Рис. 49

Система имеет одну степень свободы. В качестве обобщенной координаты возьмем угол 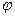поворота цилиндра. Точка D является мгновенным центром скоростей. При малых колебаниях её можно считать неподвижной. В решении задачи ничего не изменится, если в точке D ввести неподвижный шарнир. Колебания можно считать малыми до тех пор, пока можно считать постоянными углы наклона пружин к плоскости.

Перемещения точек при малых колебаниях направлены по скоростям этих точек. Причем для малых перемещений также выполняется теорема о равенстве проекций. Например, в нашей задаче:

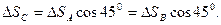
Итак, сообщим цилиндру бесконечно малый поворот 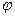вокруг точки D. Производная 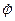будет угловой скоростью. Кинетическая энергия найдется по формуле:

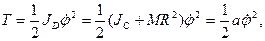
где .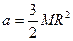

Потенциальная энергия вызывается силами упругости двух пружин. Перемещения точек A и B:

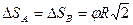
направлены по осям пружин; 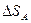- удлинение, 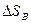- осадка. Отсюда следует:

,

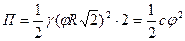где .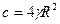

Период малых колебаний равен:

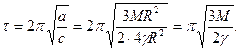
Дата добавления: 2015-06-27