Понятие об устойчивости равновесия

Колебания системы будут оставаться малыми, если они совершаются в окрестности её устойчивого положения равновесия. Устойчивость есть либо стремление системы вернуться в исходное положение, после того как она из него была выведена, либо как способность пребывать вблизи этого исходного положения. В первом случае устойчивость называют асимптотической, во втором – обыкновенной. Если же система, после того как её точкам сообщили малые смещения и скорости, еще далее начинает уходить от положения равновесия, то её положение равновесия будет называться неустойчивым. Строгое понятие устойчивости и неустойчивости дано А. М. Ляпуновым - / /.

На рис. показан пример – шарик на гладкой поверхности.

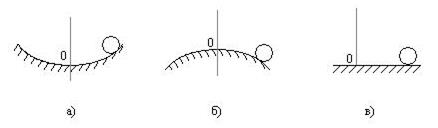
Рис. 46

Нетрудно оценить его состояние равновесия в отношении устойчивости. В случае а) равновесие устойчиво, в случае б) – неустойчиво. Случай в) является особенным. Здесь шарик безразличен к смещениям, но неустойчив относительно скоростей. Подобные системы изучаются в теории устойчивости движения.

Достаточный признак устойчивости равновесия консервативной системы сформулирован в теореме Лагранжа-Дирихле: если в положении равновесия потенциальная энергия системы имеет минимум, то равновесие устойчиво.

Отсюда следует, что вопрос об устойчивости сводится к изучению структуры выражения потенциальной энергии.

.

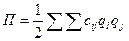10.3

В положении равновесия П = 0. Чтобы нулевое значение было минимумом, функция П в окрестности этой точки должна быть определенно положительной квадратичной формой. Оценочным критерием определенной положительности квадратичной формы являются неравенства Сильвестра.

.

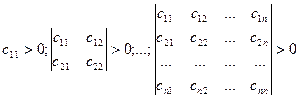10.4

Данные неравенства можно трактовать как условия устойчивости положения равновесия консервативной системы.

Примеры.

1. Однородный брусок заданных размеров и веса положен на цилиндр заданного радиуса. Относительное перемещение бруска и цилиндра происходит при чистом качении. Выяснить, при каком условии равновесие бруска на цилиндре будет устойчивым?

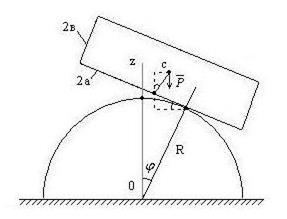
Рис. 47

Сообщим системе перемещение и составим выражение потенциальной энергии силы тяжести:

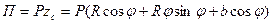
(1)

Равновесие устойчиво, если:

.

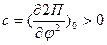(2)

Из (1) находим производные:

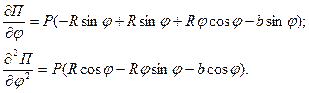
Отсюда при 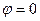получаем условие устойчивости:

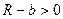
(3)

На рис. показаны возможные случаи устойчивости и неустойчивости.

Рис. 48

Дата добавления: 2015-06-27