
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Равносильность формул алгебры высказываний
|
|
|
|
Равносильность формул алгебры высказываний. Свойства отношения равносильности: рефлексивность, симметричность, транзитивность. Основные равносильности, определяющие свойства логических операций над формулами (законы алгебры высказываний).
Правила равносильных преобразований формул алгебры высказываний (правилo подстановки). Методы доказательства равносильности формул: посредством равносильных преобразований и с помощью таблицы истинности. Совместность множества формул. Упрощение систем высказываний.
10.1. Доказать, что на множестве формул алгебры высказываний отношение равносильности формул является отношением эквивалентности.
10.2. Доказать законы алгебры высказываний:
1)  закон тождества;
закон тождества;
2) 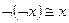 закон двойного отрицания;
закон двойного отрицания;
3) 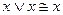 и
и  законы идемпотентности;
законы идемпотентности;
4) 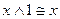 ,
, 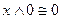 и
и 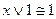 ,
, 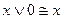 ;
;
5) 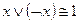 закон исключенного третьего;
закон исключенного третьего;
6)  закон противоречия;
закон противоречия;
7) 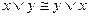 и
и 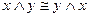 законы коммутативности;
законы коммутативности;
8)  и
и  законы ассоциативности;
законы ассоциативности;
9) 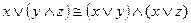 законы
законы
и 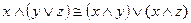 дистрибутивности;
дистрибутивности;
10) 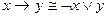 закон замены импликации;
закон замены импликации;
11) 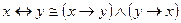 закон удаления эквиваленции;
закон удаления эквиваленции;
12) 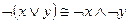 и
и 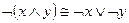 законы де Моргана;
законы де Моргана;
13)  и
и 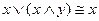 законы поглощения;
законы поглощения;
14)  и
и 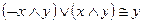 законы склеивания;
законы склеивания;
15) 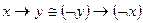 закон контрапозиции;
закон контрапозиции;
16)  закон силлогизма;
закон силлогизма;
17) 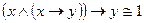 закон заключения.
закон заключения.
10.3. Докажите равносильность следующих формул двумя способами: посредством равносильных преобразований и с помощью таблиц истинности:
1) 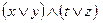 и
и 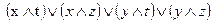 ;
;
2)  и
и 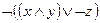 ;
;
3) 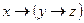 и
и 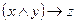 ;
;
4) 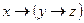 и
и 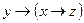 ;
;
5) 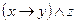 и
и 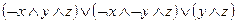 ;
;
6)  и
и  ;
;
7)  и
и  ;
;
8)  и
и 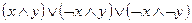 ;
;
9) 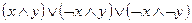 и
и 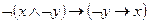 .
.
10.4. Доказать, что существует 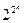 неэквивалентных формул от
неэквивалентных формул от 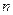 переменных.
переменных.
10.5. Пусть формулы 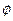 и
и 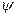 эквивалентны и
эквивалентны и 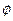 является подформулой формулы
является подформулой формулы 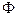 . Доказать, что если формула
. Доказать, что если формула  получена из формулы
получена из формулы 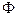 подстановкой вместо подформулы
подстановкой вместо подформулы 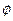 формулы
формулы 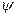 , то
, то 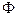 и
и  эквивалентны.
эквивалентны.
10.6. Упростить следующие формулы посредством равносильных преобразований:
1) 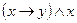 ;
;
2) 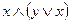 ;
;
3)  ;
;
4) 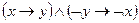 ;
;
5) 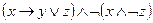 ;
;
6)  ;
;
7)  ;
;
8) 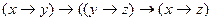 ;
;
9) 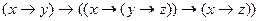 .
.
10.7. Определить, на каких наборах значений переменных следующие формулы ложны:
1) 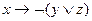 ;
;
2) 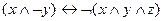 ;
;
3) 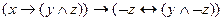 ;
;
4) 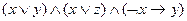 ;
;
5) 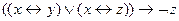 .
.
10.8. Доказать, что если формулы  и
и 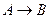 тождественно истинны, то формула
тождественно истинны, то формула 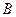 тождественно истинна.
тождественно истинна.
10.9. Доказать, что если формулы 
 и
и 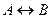 тождественно истинны, то формула
тождественно истинны, то формула 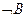 тождественно ложна.
тождественно ложна.
10.10. Доказать, что если формулы 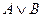 и
и 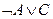 тождественно истинны, то формула
тождественно истинны, то формула 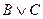 тождественно истинна.
тождественно истинна.
10.11. Доказать, что если формулы 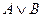 ,
,  и
и 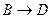 тождественно истинны, то формула
тождественно истинны, то формула 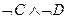 тождественно ложна.
тождественно ложна.
10.12. Доказать, что если 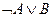 ,
,  тождественно истинны, то формула
тождественно истинны, то формула 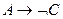 тождественно истинна.
тождественно истинна.
10.13. Пусть буквы  ,
, 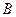 ,
,  обозначают суждения:
обозначают суждения:
 – «Множество рациональных чисел счетно»,
– «Множество рациональных чисел счетно»,
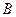 – «Множество рациональных чисел конечно»,
– «Множество рациональных чисел конечно»,
 – «Множество комплексных чисел счетно».
– «Множество комплексных чисел счетно».
Переведите на обычный язык следующие формулы: 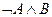 ,
, 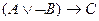 ,
, 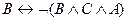 ,
, 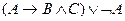 . Определите их истинность.
. Определите их истинность.
10.14. Формализовать утверждения и привести их по возможности к более простому виду:
1) Если функция непрерывна в данной точке, то она не имеет в ней разрыва; функция имеет разрыв в данной точке.
2) Либо Санчо Панса станет губернатором, либо Дон Кихот – не доблестный рыцарь, а Дон Кихот – доблестный рыцарь, так как Дульцинея Тобосская любит только доблестных рыцарей.
3) Если треугольник равносторонний, то все углы в треугольнике равны или все его высоты имеют одинаковую длину; и неверно, что треугольник равносторонний, но высоты треугольника не равны.
4) Необходимым условием победы спортсмена является его хорошая физическая форма.
5) Хорошей физической формы спортсмена не достаточно для его победы.
6) Чтобы быть допущенным к экзамену необходимо и достаточно сдать зачет.
7) Чтобы сдать экзамен, необходимо, но не достаточно сдать зачет.
8) Чтобы улучшить состояние здоровья достаточно, но не необходимо съездить на море.
9) Отрезки 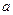 ,
, 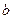 ,
, 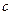 являются сторонами треугольника, если
являются сторонами треугольника, если  , но для того чтобы отрезки
, но для того чтобы отрезки 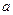 ,
, 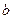 ,
, 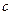 не являлись сторонами треугольника, необходимо, чтобы
не являлись сторонами треугольника, необходимо, чтобы  .
.
10) Чтобы Боб был счастлив, достаточно, чтобы ему купили велосипед или отпустили в кино; чтобы Боб был счастлив и его отпустили в кино, необходимо, чтобы ему купили велосипед; Боб счастлив, так как ему купят велосипед и отпустят в кино.
10.15. До царя Гороха дошла молва, что кто-то из троих богатырей убил Змея Горыныча. Царь приказал всем троим явиться ко двору и молвили они:
Илья Муромец: «Змея убил Добрыня Никитич»;
Добрыня Никитич: «Змея убил Алеша Попович»;
Алеша Попович: «Я убил Змея».
При этом известно, что один из них сказал правду, а двое слукавили. Кто убил змея?
10.16. В велогонках приняли участие пять школьников. После гонок пять болельщиков заявили:
«Коля занял первое место, а Ваня – четвертое»;
«Сережа занял второе место, а Ваня – четвертое»;
«Сережа занял второе место, а Коля – третье»;
«Толя занял первое место, а Надя – второе»;
«Надя заняла третье место, а Толя – пятое».
Зная, что одно из показаний каждого болельщика верное, а другое - неверное, найти правильное распределение мест.
10.17. В стране Чудес проводилось следствие по делу об украденной муке. На суде Мартовский Заяц заявил, что муку украл Болванщик. В свою очередь Болванщик и Соня дали показания, которые по каким-то причинам не были записаны. В ходе судебного заседания выяснилось, что муку украл лишь один из трех подсудимых и что только он дал правдивые показания. Кто украл муку?
|
|
|
|
|
Дата добавления: 2015-06-27; Просмотров: 2172; Нарушение авторских прав?; Мы поможем в написании вашей работы!