
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Нормальные формы формул алгебры высказываний
|
|
|
|
Элементарная конъюнкция (ЭК), элементарная дизъюнкция (ЭД) от высказывательных переменных. Свойство ЭК (ЭД) принимать значение 1 (0) ровно на одном наборе значений переменных. Конъюнктивная нормальная форма (КНФ) и дизъюнктивная нормальная форма (ДНФ) формулы алгебры высказываний. Критерии существования КНФ и ДНФ. Алгоритмы построения различных КНФ и ДНФ для заданной формулы. Критерий тождественной истинности (ложности) формул алгебры высказываний, основанный на свойствах ЭД и КНФ (ЭК и ДНФ).
13.1. Указать элементарные конъюнкции и элементарные дизъюнкции среди следующих формул:
1) 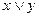 ; 5)
; 5) 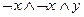 ;
;
2)  ; 6)
; 6) 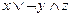 ;
;
3) 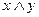 ; 7)
; 7) 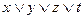 ;
;
4) 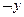 ; 8)
; 8) 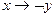 .
.
13.2. Доказать, что каждая элементарная конъюнкция истинна, а каждая элементарная дизъюнкция ложна только на одном наборе истинностных значений входящих в нее переменных.
13.3. Установить, какие из данных формул являются элементарными конъюнкциями, элементарными дизъюнкциями, КНФ и ДНФ:
1)  ; 6)
; 6) 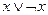 ;
;
2) 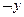 ; 7)
; 7) 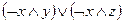 ;
;
3) 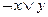 ; 8)
; 8) 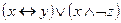 ;
;
4) 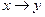 ; 9)
; 9) 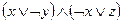 ;
;
5) 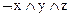 ; 10)
; 10) 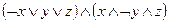 .
.
13.4. В упражнении 13.3. определить для элементарных конъюнкций и ДНФ наборы значений переменных, на которых они принимают значение 1; для элементарных дизъюнкций и КНФ – наборы, на которых они принимают значение 0.
13.5. Построить различные элементарные конъюнкции, содержащие
а) одну; б) две; в) три
из переменных  ,
, 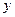 ,
, 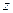 и являющиеся истинными на каждом из следующих наборов:
и являющиеся истинными на каждом из следующих наборов:
1) 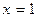 ,
, 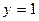 ,
, 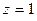 ;
;
2) 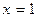 ,
, 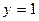 ,
, 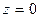 ;
;
3) 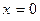 ,
,  ,
, 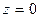 .
.
13.6. Построить различные элементарные дизъюнкции, содержащие
а) одну; б) две; в) три
из переменных  ,
, 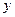 ,
, 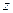 и являющиеся ложными на каждом из следующих наборов:
и являющиеся ложными на каждом из следующих наборов:
1) 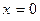 ,
,  ,
, 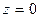 ;
;
2) 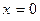 ,
, 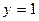 ,
, 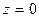 ;
;
3) 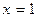 ,
, 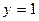 ,
, 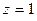 .
.
13.7. Построить различные КНФ, являющиеся ложными на следующих наборах значений переменных  ,
, 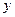 ,
, 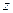 :
:
1) 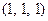 ,
, 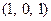 ;
;
2) 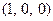 ,
, 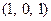 ,
, 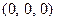 ;
;
3) 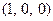 .
.
13.8. Построить различные ДНФ, являющиеся истинными на наборах значений переменных  ,
, 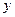 ,
, 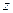 , приведенных в упражнении 13.7.
, приведенных в упражнении 13.7.
13.9. Следующие формулы преобразовать так, чтобы они содержали только операции 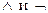 :
:
1) 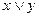 ;
;
2) 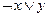 ;
;
3) 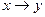 ;
;
4) 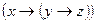 ;
;
5) 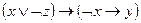 .
.
13.10. Следующие формулы преобразовать так, чтобы они содержали только операции 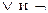 :
:
1) 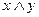 ;
;
2) 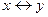 ;
;
3) 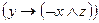 ;
;
4) 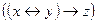 .
.
13.11. Следующие формулы преобразовать так, чтобы они содержали только операции 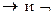 :
:
1) 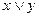 ;
;
2) 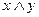 ;
;
3) 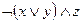 ;
;
4) 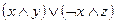 .
.
13.12. Доказать, что следующие системы связок являются полными, то есть для любой формулы существует эквивалентная ей формула, содержащая логические связки только из заданной системы:
1) 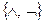 ;
;
2)  ;
;
3) 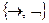 .
.
13.13. Доказать, что системы связок
1) 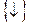 ;
;
2) 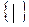
где 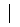 – штрих Шеффера (или дизъюнкция отрицаний):
– штрих Шеффера (или дизъюнкция отрицаний): 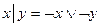 ,
,
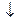 – стрелка Пирса (или конъюнкция отрицаний):
– стрелка Пирса (или конъюнкция отрицаний): 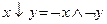 ,
,
являются полными.
13.14. Доказать, что следующие системы связок не являются полными, то есть, не достаточны для выражения любой формулы:
1) 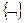 ;
;
2) 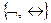 ;
;
1) 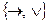 .
.
13.15. Следующие формулы преобразовать так, чтобы отрицание относилось только к высказывательным переменным:
1) 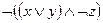 ;
;
2) 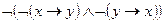 ;
;
3) 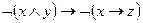 ;
;
4) 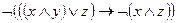 .
.
13.16. Следующие формулы преобразовать так, чтобы они содержали только операции 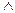 ,
, 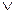 ,
, 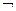 , при этом
, при этом 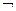 относилось только к высказывательным переменным:
относилось только к высказывательным переменным:
1) 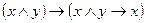 ;
;
2) 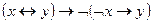 ;
;
3) 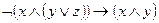 ;
;
4) 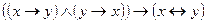 .
.
13.17. Приведите следующие формулы к различным КНФ и различным ДНФ с помощью равносильных преобразований:
1) 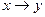 ; 7)
; 7) 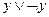 ;
;
2) 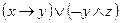 ; 8)
; 8) 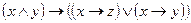 ;
;
3) 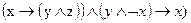 ; 9)
; 9)  ;
;
4) 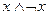 ; 10)
; 10) 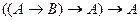 ;
;
5) 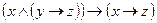 ; 11)
; 11) 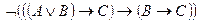 ;
;
6) 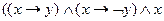 ; 12)
; 12) 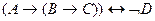 .
.
13.18. Показать, что для любой формулы существует бесконечное множество различных КНФ и ДНФ.
13.19. Указать тип формул упражнения 13.17., используя критерии тождественной истинности и тождественной ложности формул, основанные на свойствах элементарной дизъюнкции и КНФ; элементарной конъюнкции и ДНФ.
13.20. Может ли Андрей получить 3, а Миша 4, если известно, что каждое из приведенных ниже высказываний истинно:
а) Коля получил 5 или Нина не получила 4;
б) Нина получила 4 или Андрей не получил 3;
в) Маша не получила 4 или Даша получила 2;
г) Даша не получила 2 или Володя не получил 4;
д) Коля не получил 5 или Володя получил 4.
13.21. При составлении расписания уроков на один день учителя математики, истории и литературы высказали следующие пожелания: математик просил поставить ему или первый, или второй урок; историк – или первый, или третий; учитель литературы – или второй, или третий. Как составить расписание уроков, чтобы учесть все пожелания?
13.22. (Задача Венна.) Существовал финансовый клуб с такими правилами:
а) Члены финансового комитета должны избираться среди членов общей дирекции.
б) Нельзя быть одновременно членом общей дирекции и членом библиотечного совета, не будучи членом финансового комитета.
в) Ни один член библиотечного совета не может быть членом финансового комитета.
Упростить правила.
13.23. (Задача Кислера.) Браун, Джонс и Смит обвиняются в подделке сведений о подлежащих налоговому обложению доходах. Они дают следующие показания под присягой:
Браун: Джонс виновен, а Смит невиновен.
Джонс: Если Браун виновен, то виновен и Смит.
Смит: Я невиновен, но хотя бы один из них двоих виновен.
Ответить на вопросы:
а) Совместимы ли показания всех троих одновременно?
б) Показания одного из обвиняемых следуют из показаний другого; о чьих показаниях идет речь?
в) Если все трое невиновны, то кто совершил лжесвидетельство?
г) Предполагая, что показания всех обвиняемых верны, указать, кто виновен, а кто невиновен?
д) Если невиновный говорит истину, а виновный лжет, то кто невиновен, а то виновен?
|
|
|
|
|
Дата добавления: 2015-06-27; Просмотров: 949; Нарушение авторских прав?; Мы поможем в написании вашей работы!