
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Совершенные нормальные формы формул алгебры высказываний
|
|
|
|
Полная элементарная конъюнкция (ПЭК) и полная элементарная дизъюнкция (ПЭД). Совершенная конъюнктивная нормальная форма (СКНФ) и совершенная дизъюнктивная нормальная форма (СДНФ). Критерии существования и единственности СКНФ и СДНФ. Алгоритмы преобразования элементарной конъюнкции к конъюнкции полных элементарных дизъюнкций, элементарной дизъюнкции – к дизъюнкции полных элементарных конъюнкций. Алгоритмы построения ПЭК (ПЭД), истинной (ложной) на данном наборе значений переменных. Алгоритмы построения СКНФ (СДНФ) для заданной опровержимой (выполнимой) формулы: построение с помощью равносильных преобразований, построение с помощью таблицы истинности. Алгоритмы перехода от СКНФ к СДНФ и обратно для формул, являющихся одновременно опровержимыми и выполнимыми. Правила вычисления истинностных значений ПЭК, СДНФ и ПЭД, СКНФ в соответствии с их определениями. Критерий равносильности формул, основанный на свойствах СДНФ и СКНФ.
14.1. Установить, какие из данных формул являются элементарными конъюнкциями, элементарными дизъюнкциями, полными элементарными конъюнкциями, полными элементарными дизъюнкциями, КНФ, ДНФ, СКНФ, СДНФ от одной, двух или трех переменных:
1) 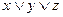 ; 6)
; 6) 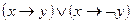 ;
;
2) 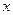 ; 7)
; 7) 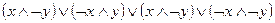 ;
;
3) 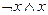 ; 8)
; 8) 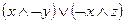 ;
;
4) 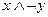 ; 9)
; 9) 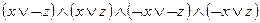 ;
;
5) 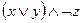 ; 10)
; 10) 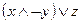 .
.
14.2. Построить различные элементарные конъюнкции (дизъюнкции) от высказывательных переменных 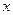 ,
, 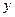 ,
, 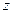 .
.
14.3. Построить различные полные элементарные конъюнкции (дизъюнкции) от высказывательных переменных 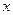 ,
, 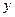 ,
, 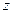 .
.
14.4. Следующие элементарные конъюнкции (элементарные дизъюнкции) преобразовать в конъюнкции полных элементарных дизъюнкций (полных элементарных конъюнкций) от трех переменных:
1) 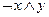 ;
;
2) 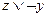 ;
;
3) 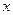 ;
;
4) 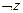 .
.
14.5. Следующие формулы привести к СКНФ и СДНФ посредством равносильных преобразований:
1) 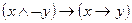 ; 6)
; 6) 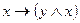 ;
;
2) 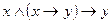 ; 7)
; 7) 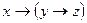 ;
;
3) 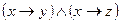 ; 8)
; 8) 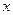 ;
;
4) 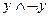 ; 9)
; 9) 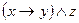 ;
;
5) 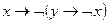 ; 10)
; 10) 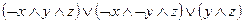 .
.
14.6. Построить полные элементарные конъюнкции и полные элементарные дизъюнкции, принимающие значение 1 и 0 соответственно только на следующем наборе значений переменных:
1) 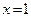 ,
, 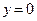 ;
;
2) 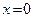 ,
, 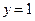 ,
, 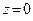 ;
;
3) 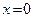 ;
;
4) 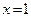 ,
, 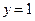 ,
, 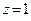 .
.
14.7. Построить СКНФ и СДНФ, принимающие соответственно значения 0 и 1 на следующих наборах значений переменных:
1) 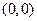 ,
, 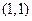 ;
;
2) 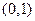 ;
;
3) 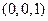 ,
, 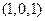 ,
, 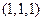 ;
;
4) 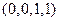 ,
, 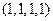 ;
;
5) 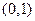 ,
, 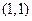 ,
, 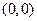 ,
, 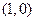 .
.
14.8. Длякаждой из формул упражнения 14.5. найти СКНФ и СДНФ, используя ее таблицу истинности.
14.9. Определить тип формулы, если известна ее СДНФ:
1) 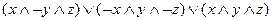 ;
;
2) 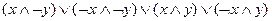 ;
;
3) СДНФ не существует;
4) 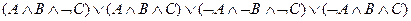 .
.
Указать наборы значений переменных, на которых формула истинна.
14.10. Определить тип формулы, если известна ее СКНФ:
1) 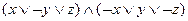 ;
;
2) 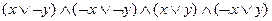 ;
;
3) СКНФ не существует;
4) 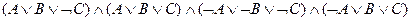 .
.
Указать наборы значений переменных, на которых формула ложна.
14.11. Построить все возможные формулы 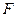 такие, чтобы следующая формула была тавтологией:
такие, чтобы следующая формула была тавтологией:
1) 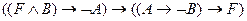 ;
;
2) 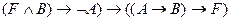 ;
;
3) 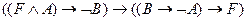 ;
;
4) 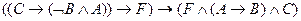 .
.
14.12. Найдите формулу от трех переменных, которая принимает такое же значение, как и большинство ее аргументов.
14.13. Найдите такую формулу от четырех переменных, которая принимает значение 1 тогда и тогда, когда ее первый аргумент принимает значение 0.
14.14. Один из трех поросят украл желудь. При расследовании этого происшествия они сделали следующие заявления:
Ниф-Ниф: Я не делал этого. Нуф-Нуф не делал этого.
Наф-Наф: Я не делал этого. Это сделал Ниф-Ниф.
Нуф-Нуф: Ниф-Ниф не делал этого. Это сделал Наф-Наф.
Как впоследствии выяснилось, один из них дважды сказал правду, другой – дважды солгал, третий – раз сказал правду, раз солгал. Кто взял желудь?
14.15. Богини Гера, Афродита и Афина пришли к юному Парису, чтобы тот установил, кто из них прекраснее всех. Они высказали следующие утверждения:
Афродита: Я самая прекрасная. Гера не самая прекрасная.
Гера: Я самая прекрасная.
Афина: Афродита не самая прекрасная. Я самая прекрасная.
Парис предположил, что все утверждения прекраснейшей из богинь истинны, а все утверждения двух остальных ложны. Кого назвал прекраснейшей Парис?
14.16. На судекаждый из троих подсудимых обвинял одного из двух других. Оказалось, что первый из них был единственным, кто говорил правду. Если бы каждый стал обвинять другого из них (но не себя), то второй был бы единственным, кто сказал правду. Кто виновен?
В следующих задачах (14.17. – 14.19.) кроме уже известных рыцарей и лжецов (см. примечание к задачам 12.11. – 12.15.) на острове появляются хитрецы – те, кто иногда говорят правду, а иногда лгут.
14.17. Из трех жителей К, М и Р отдаленного района один является рыцарем, один – лжецом, а третий – хитрецом. Они произнесли следующие утверждения:
К: «Я – хитрец»;
М: «Это правда»;
Р: «Я не хитрец».
Кто есть кто?
14.18. Три аборигена: А, Б, С (рыцарь, лжец и хитрец) – на вопрос: «Кто Б?» – ответили:
А: «Лжец»;
Б: «Я хитрец»;
С: «Рыцарь».
Кто рыцарь и кто хитрец?
14.19. Двое людей, К и М, о которых известно, что каждый из них либо рыцарь, либо лжец, либо хитрец, утверждают:
К: «М – рыцарь»;
М: «К – рыцарь».
Докажите, что по меньшей мере один из них говорит правду и является хитрецом.
14.20. После представления «Ревизора» состоялся диалог.
Бобчинский: «Это Вы, Петр Иванович, первый сказали «Э!». Вы сами так говорили».
Добчинский: «Нет, Петр Иванович, я так не говорил. Это Вы семгу первый заказали. Вы и сказали «Э!». А у меня зуб во рту со свистом».
Бобчинский: «Что я семгу первый заказал, это верно. И верно, что у Вас зуб со свистом. А все-таки, это Вы первый сказали «Э!».
Выясните, кто первым сказал «Э!», если известно, что из девяти произнесенных в этом диалоге утверждений четное число верных.
|
|
|
|
|
Дата добавления: 2015-06-27; Просмотров: 1658; Нарушение авторских прав?; Мы поможем в написании вашей работы!