По закону парности касательных напряжений

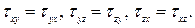
(3.1)

Таким образом, напряженное состояние в точке тела определяется шестью напряжениями. Эти напряжения объединены в комплексный показатель – тензор напряжений

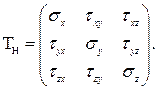
В силу гипотезы о сплошности материала каждое напряжение является функцией координат точки, т. е.

.

Тензор напряжений, определяемый выражением (3.2), является тензором второго ранга, симметричным (в силу соотношений (3.1)) относительно главной диагонали. Это свойство позволяет получить при анализе напряженного состояния ряд важных соотношений.

Установлено, что если известны напряжения в трех взаимно перпендикулярных площадках, проходящих через исследуемую точку, то напряжение в этой точке может быть определено однозначно. Для этого получены формулы, определяющие составляющие 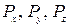полного напряжения 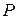в наклонной площадке, расположенной бесконечно близко к рассматриваемой точке. Ориентация наклонной площадки задается направляющими косинусами 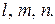[ 7 ].

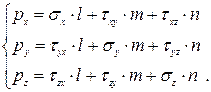(3.3)

Нормальное напряжение в наклонной площадке определяется соотношением [7]

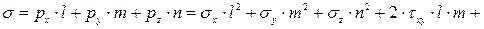
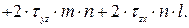(3.4)

Касательное напряжение, действующее в наклонной площадке, определяется из выражения [ 7 ]

(3.5)

Наклонная площадка может иметь такую ориентацию, что в ней будут действовать только нормальные или только касательные напряжения. Площадки, на которых отсутствуют касательные напряжения, называют главными площадками, а действующие на них напряжения – главными. Доказано, что через каждую точку тела можно провести единственные три взаимно перпендикулярные главные площадки, в каждой из которых действует одно главное напряжение. Между главными напряжениями установлено соотношение

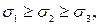(3.6)

где 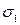- наибольшее главное напряжение; 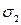- среднее главное напряжение; -
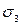наименьшее главное напряжение.

Главные напряжения определяют из характеристического уравнения [ 7 ]

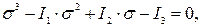(3.7)

где 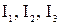- первый, второй и третий инварианты напряженного состояния.

Инварианты определяют из соотношений:

(3.8)

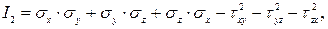(3.9)

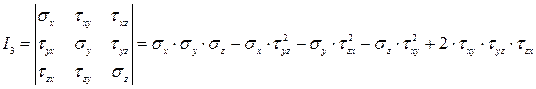(3.10)

В уравнениях (3.8) − (3.10) 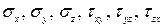- известные напряжения, действующие в трех взаимно перпендикулярных площадках, проходящих через рассматриваемую точку деформированного тела.

Главные напряжения характеризуют физическое состояние упругого тела и поэтому их величина не зависит от выбора системы отсчета (координатных осей). При поворотах осей они сохраняют для данной точки упругого тела постоянную величину. Поэтому 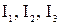названы инвариантами, т. е. при заданной внешней нагрузке их величины постоянны и определяются выражениями (3.8) − (3.10).

Положение главных площадок вычисляют из соотношений [ 7 ]

(3.11)

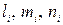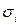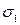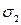Здесь - направляющие косинусы нормали v _i к главной площадке, где действует главное напряжение ( или , или ).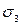

Нормали к главным площадкам образуют систему трех взаимно перпендикулярных осей, называемых главными осями напряженного состояния в точке упругого тела. Показано в [ 7 ], что решением кубического уравнения (3.7) всегда являются вещественные значения .

Область допустимых значений нормальных и касательных напряжений в произвольных площадках определяют на основании анализа соотношений

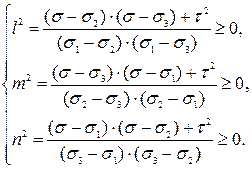(3.12)

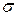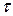с помощью круговых диаграмм Мора. Эти же диаграммы позволяют отыскивать экстремальные значения и , которые могут быть достигнуты в любой точке упругого деформированного тела.

В частности, показано, что

(3.13)

Рассмотрение уравнения (3.7) при различных значениях входящих в него инвариантов приводит к детальному анализу частных случаев трехосного (объемного) напряженного состояния:

а) двухосного (плоского),

б) одноосного (линейного).

Тензор напряжений, оценивающий физическое состояние упругого деформированного тела, представляют в виде

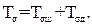(3.14)

В выражении (3.14) введены следующие обозначения:

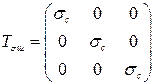– шаровой тензор напряженного состояния; (3.15)

– тензор-девиатор напряженного состояния (3.16)

где 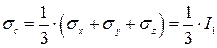(3.17)

Такое представление тензора напряжений позволяет рассматривать процесс деформирования состоящим из двух взаимосвязанных явлений – изменения объема тела (всестороннее растяжение или сжатие), которое оценивается составляющими шарового тензора, и изменения формы тела (линейные и угловые деформации) – оценивается с помощью составляющих тензора–девиатора [ 7 ].

3.2. Деформированное состояние в точке упругого тела

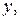
Произвольная точка тела после деформирования занимает по отношению к неподвижной системе координат новое положение, характеризующееся радиусом – вектором. Если перемещение точек в направлении осей 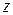обозначить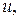

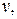
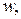
то в силу гипотезы оплошности материала тела, они будут непрерывными функциями координат:

(3.18)

Доказано [ 7 ], что деформированное состояние в каждой точке упругого тела характеризуется изменением длин отрезков, проходящих через эту точку, линейными деформациями и изменением углов между отрезками – угловыми деформациями.

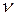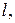
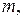
Относительная линейная деформация в произвольном направлении, характеризующемся нормалью с направляющими косинусами 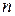, определяется из уравнения [ 7 ]

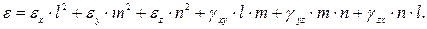(3.19)

В уравнение (3.19) введем следующие соотношения [ 7 ]:

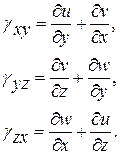(3.20)

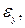
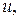
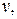
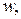Формулы (3.20) называют формулами Коши. Три первые из них определяют относительные линейные деформации , через перемещения последние – относительные угловые деформации.

Показано [7], что в некоторых направлениях, называемых главными направлениями, линейные деформации принимают экстремальные значения, которые обозначают

(3.21)

В площадках, перпендикулярных к этим главным деформациям, углы между двумя направлениями не искажаются.

Если известны главные деформации 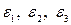, то линейная деформация в любом направлении, определяемом направляющими косинусами 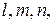и искажение пря-мого угла между направлениям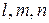и () и () выражаются формулами [ 7 ]:

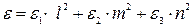
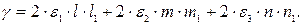(3.22)

Деформированное состояние характеризуется тензором деформаций

Известно [7], что . Поэтому тензор деформаций

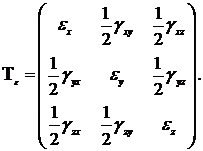(3.23)

является тензором второго ранга, симметричным относительно главной диагонали, что позволяет при анализе деформированного состояния сделать ряд важных выводов.

Главные деформации 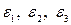отыскивают из решения характеристического уравнения

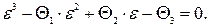(3.24)

В уравнении (3.24) введены следующие обозначения:

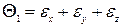(3.25)

- первый инвариант деформированного состояния

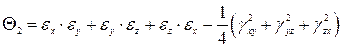(3.26)

- второй инвариант деформированного состояния;

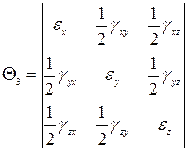(3.27)

- третий инвариант деформированного состояния.

Составляющие тензора зависят от направления координатных осей, но выражения (3.2) − (3.27) не изменяются при повороте координатных осей, поэтому и называются инвариантами.

Известно, что 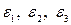- всегда вещественные корни уравнения (3.24).

Как и при напряженном, при деформированном состоянии анализ уравнения (3.24) при определенных значениях 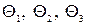приводит к частным случаям:

а) плоскому (двухосному),

б) линейному (одноосному).

Основные соотношения деформаций в каждом из частных деформированных состояний определены и приводятся, например, в [ 7 ].

Деформации должны удовлетворять следующим соотношениям:

(3.28)

Эти зависимости называют условиями Сен-Венана (условиями совместности деформаций). Их геометрический смысл состоит в следующем. Предположим, что тело в начальном состоянии разложено на элементарные параллелепипеды. Деформации ребер и углов каждого элемента должны удовлетворять условиям (3.28), иначе из деформированных элементов нельзя составить сплошного (неразрывного) деформированного тела.

3.3. Закон Гука

Между составляющими тензора напряжений и тензора деформаций существуют зависимости, которые для материалов с различными физическими свойствами определены опытным путем. Для малых деформаций (в сравнении с размерами деформируемых тел) эти зависимости представлены линейными функциями.

Физические свойства, которые обнаруживаются в испытываемых образцах при различных видах нагружений, называют механическими свойствами материала. В рамках принятой модели твердого деформируемого тела результаты испытаний распространены для изотропных материалов, т. е. таких, у которых механические свойства не зависят от ориентации вырезанного из них для испытаний образца.

Экспериментально установлено, что если образец растягивается в одном направлении, что порождает действие в этом же направлении напряжения 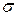, то происходит его удлинение. Пусть - относительная деформация в направлении действия . Относительная деформация в любом перпендикулярном действию 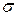направлении, ведет к сокращению поперечных размеров. Опытным путем установлено, что при этом имеют место соотношения:

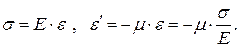(3.29)

Постоянная 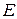называется модулем упругости или модулем Юнга, или модулем упругости первого рода. Постоянную 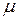- называют коэффициентом Пуассона или коэффициентом поперечной деформации. Доказано, что

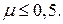(3.30)

Знак равенства имеет место для несжимаемых тел, модель которых используют в теории пластического течения материала.

Формула (3.29) определяет закон Гука при одноосном напряженном состоянии.

Если к телу приложить нагрузки одновременно в трех взаимно перпендикулярных направлениях, вызывающих появление 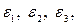то получим

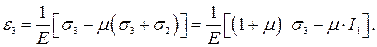(3.31)

Зависимости (3.31) устанавливают связь между главными напряжениями и главными деформациями.

Когда на гранях образцов действуют не только нормальные, но и касательные напряжения, приходим к зависимостям вида

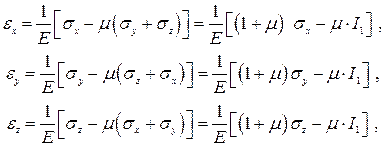
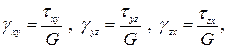(3.32)

где 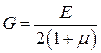- модуль сдвига или модуль упругости второго рода.

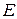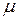Формулы (3.32) выражают обобщенный закон Гука для изотропного упругого тела, механические свойства которого характеризуются двумя постоянными: и , определяемыми при растяжении (реже при сжатии).

При решении ряда задач о упругом деформировании обобщенный закон Гука удобно представлять следующими соотношениями:

(3.33)

где 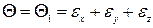- первый инвариант деформированного состояния в точке тела;

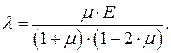
Коэффициенты 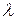и при таком представлении обобщенного закона Гука называют постоянными Ляме.

При решениях частных задач используют соотношения

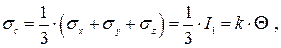(3.34)

где - объемный модуль упругости.

Для анизотропного материала (т. е. такого, у которого механические свойства по разным направлениям различны) сохраняется линейная зависимость между напряжениями и деформациями, но число упругих постоянных возрастает [17].

В самом общем случае анизотропии число упругих постоянных равно 21. У анизотропных тел линейные деформации возникают от действия касательных напряжений, а угловые деформации могут возникать при действии нормальных напряжений.

3.4 Теории предельных состояний

Для безопасной работы любой конструкции необходимо, чтобы все ее детали выдерживали рабочие нагрузки без разрушения или пластических деформаций. Напряженное состояние, при котором происходит разрушение материала или начинается его пластическое деформирование, называется предельным.

Наиболее просто предельное состояние установить при линейном напряженном состоянии, для чего образцы из различных материалов подвергают одноосному растяжению (реже сжатию).

При таких опытах образцы подвергаются воздействию возрастающей нагрузки до их разрушения. В ходе испытаний измеряются нагрузка на образец и его абсолютное удлинение, определяемое на определенной длине (базе). Одновременно записывается диаграмма “ 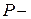∆ 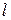”, где 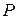- растягивающее усилие, ∆ 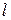- абсолютное

удлинение образца ∆ 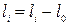. Затем строится диаграмма “ ”, где 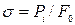- нормальные напряжения ( - текущие значения растягивающей силы, 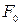- первоначальная площадь поперечного сечения образца), 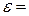∆ 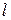/ 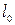- относительное удлинение образца в каждый момент растяжения ( 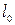- исходная длина базы).

Диаграммы деформирования всех материалов можно отнести к одному из трех основных типов (рис. 3.1).

До точки “а” на диаграммах соблюдается закон Гука, т. е. выдерживается линейная зависимость между напряжениями и деформациями.

Тип диаграммы (рис 3.1а) соответствует образцам из низкоуглеродистых сталей различных марок. Для такой диаграммы характерно наличие площадки текучести (участок “вс”). Напряжение 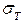называют пределом текучести. Разгрузка образца и его повторное растяжение приводят к повышению величины 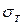. Напряжение, соответствующее максимальной нагрузке на образец называют пределом прочности .

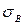Диаграмма (рис.3.1б) соответствует цветным металлам и сплавам, легированным сталям. На этой диаграмме отсутствует площадка текучести. Поэтому определяют условный предел текучести 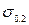(реже 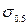), соответствующий относительной линейной деформации 0.2 % (0.5 %).

Такие конструкционные материалы, как чугун, закаленные стали, керамические материалы, бетон, имеют свою диаграмму деформирования (3.1в). Главной ее особенностью является отсутствие развитых пластических деформаций при разрушении образца. Такие материалы называют хрупкими, для них определяют только предел прочности.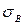

При линейном напряженном состоянии для пластичных материалов предельное напряжение равно пределу текучест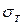и или 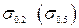, а для хрупких – пределу прочности 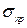. Если материал какой-либо детали испытывает линейное напряженное состояние, то условием его нормальной (безопасной) работы является выполнение неравенства

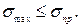(3.35)

Максимальное напряжение должно быть меньше предельного по следующим причинам:

1) рабочие нагрузки, действующие на детали, определяются приближенно, они могут иметь случайный характер;

2) механические свойства материалов имеют определенный разброс;

3) по указанным причинам предельные напряжения определяются с некоторой погрешностью.

Эти обстоятельства, а также ряд других приводят к тому, что максимальные напряжения 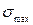должны быть значительно меньше предельных .

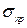На основании анализа работы существующих конструкций, с учетом условий их эксплуатации, устанавливают степень уменьшения предельных напряжений с гарантией нормальной работы конструкции.

Максимальное напряжение, при котором гарантирована нормальная (безопасная) работа конструкции, называется допускаемым напряжением и обозначается [ 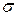]. Отношение называется коэффициентом запаса прочности. Его величина для различных конструкций и материалов устанавливается отраслевыми нормами в зависимости от условий работы и степени ответственности конструкции. С учетом изложенного условие прочности можно представить в виде

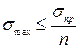или (3.36)

Оценка прочности материалов при сложном напряженном состоянии сопряжена с определенными принципиальными трудностями. В настоящее время они устраняются с помощью гипотез (теорий) о преимущественном влиянии какого-либо фактора (или группы факторов) на переход материала в предельное состояние. Такие гипотезы получили название теорий (гипотез) прочности.

Каждая теория прочности ставит в соответствие сложному напряженному состоянию, реально реализующемуся в конкретных условиях нагружения, линейное напряженное состояние (что достаточно просто оценить экспериментально), характеризующееся эквивалентным напряжением 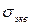. Сложное напряженное состояние и линейное будут равноопасны, т. е. будут иметь равные коэффициенты запаса прочности, если у них равны факторы, определяющие предельное состояние. После определения 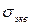расчет проводят путем сопоставления эквивалентного и допускаемого напряжений.

Наиболее употребительные теории (гипотезы) прочности будут рассмотрены ниже.

3.5. Интегральные характеристики напряжений в сечениях

В сечении тела плоскостью, перпендикулярной его продольной оси, совпадающей с осью Z системы координат XYZ, силы взаимодействия частей тела можно привести к главному вектору 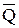и к главному моменту 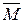, поместив центр их приведения в произвольную точку сечения. Составляющие этих векторов –

поперечные силы 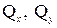, нормальное усилие 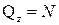, изгибающие моменты 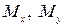и крутящий момент 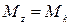- можно выразить через напряжения 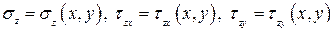, действующие в произвольной точке А с координатами (x, y). В окрестности точки А следует выделить элементарную площадку 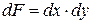(рис. 3.2). Тогда

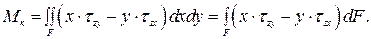(3.37)

Выражения (3.37) называют интегральными характеристиками напряжений (ИХН) в сечении. Рассекая тело плоскостями, перпендикулярными к осям “ ” и “ 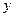” получают аналогичные выражения.

При конкретных условиях нагружения эти соотношения позволяют определить пригодные для практических расчетов формулы. К примеру, напряжение 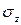входит

в выражения 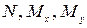. Установим зависимость между этими величинами. В конкретном сечении 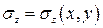. Запишем напряжение 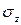в виде полинома

(3.38)

где 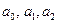-постоянные коэффициенты, требующие определения.

Подставив (3.38) в выражения (3.37) для 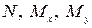, получим

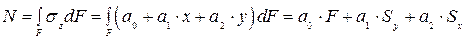(3.39)

(3.40)

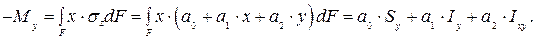(3.41)

В уравнениях (3.39) - (3.41) 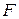- площадь сечения; 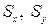- статические моменты сечения относительно осей 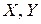; 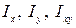- осевые и центробежный моменты инерции сечения.

Если оси координат XYZ выбрать не произвольными, а главными центральными, то 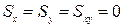, и из выражений (3.39) - (3.41) определим, что

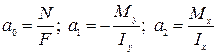(3.42)

Подставив коэффициенты 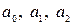из (3.42) в (3.38), получим

(3.43)

С помощью формулы (3.43) определяют нормальные напряжения в любой точке сечения с координатами 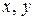; ее часто используются при расчетах, в частности при рассмотрении растяжения (сжатия), плоского поперечного изгиба, косого изгиба, изгиба с растяжением (сжатием).

Для оценки прочности материала, имеющего определенные механические свойства, необходимо знать все составляющие тензора напряжений, но для построения этих функций уравнений (3.37) недостаточно. Необходимо построить полную математическую модель деформирования твердого упругого тела, включающую следующие составные части:

1) уравнения равновесия для каждого элемента тела, получаемые на основании общих принципов механики;

2) геометрические (кинематические) соотношения между деформациями и перемещениями; для малых деформаций эти соотношения выражаются формулами Коши (3.20);

3) физические зависимости между напряжениями и деформациями; для изотропных упругих тел эти зависимости выражаются формулами (3.31) или (3.32);

4) граничные и начальные условия (при действии динамических и импульсных нагрузок), которым должны удовлетворять перемещения, напряжения и деформации на поверхностях, ограничивающих тело.

Дата добавления: 2015-06-28