Тогда прогиб

После интегрирования получим

,

или

,

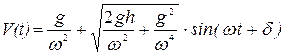где - сдвиг фаз.

Найдем частоту свободных колебаний систе-

мы, для чего вычислим предварительно .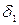

    Рис. 7.8    

.

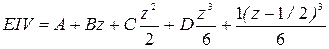Найдем постоянные из граничных условий.

1) 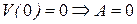, 2) ,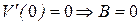

3) ,

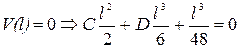4) ,

.

,

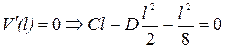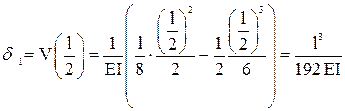а частота собственных колебаний

.

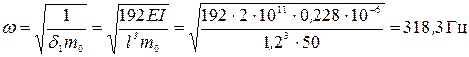Определим амплитуду колебаний относительно положения равновесия, соответ-ствующего прогибу :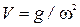

.

В заключение отметим, что расчет продольных и крутильных колебаний может быть выполнен аналогично рассмотренным расчетам поперечных колебаний, пос-кольку все они описываются одинаковыми дифференциальными уравнениями.

Так, для крутильных колебаний математической моделью является уравнение 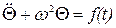, а для продольных – .

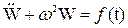7.2. Колебания систем с бесконечным числом степеней свободы

Примером стержневой системы с бесконечным числом степеней свободы может служить любая упругая система с распределенной массой. Такие системы целесооб-разно разбить на две группы: системы, совершающие продольные или крутильные колебания, и системы, совершающие поперечные колебания.

Продольные и крутильные колебания

Продольные и крутильные свободные колебания стержней описываются подоб-ными дифференциальными уравнениями. Для продольных колебаний стержней с постоянным поперечным сечением

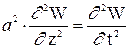, (7.3)

где 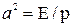; 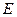- модуль Юнга; - масса единицы объема.

Для крутильных колебаний

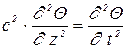, (7.4)

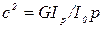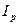где ; - модуль сдвига; - полярный момент инерции поперечного се-чения; - момент инерции единицы длины стержня.

Поскольку с математической точки зрения уравнения продольных колебаний (7.3) и крутильных (7.4) аналогичны, то и в дальнейшем будем рассматривать лишь одно из них, например уравнение продольных колебаний. Решение может быть получено методом Фурье:

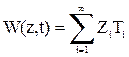, (7.5)

где 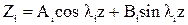- собственные формы прогибов, - собственные значения частот возмущающей силы, .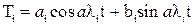

Постоянные 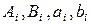должны находиться из граничных и начальных условий:

. (7.6)

Рассмотрим свободные продольные колебания стержня (рис. 7.9), вызванные предварительным смещением его правого свободного конца на величину .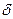

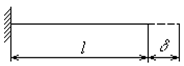    Рис. 7.9    

Из граничных условий

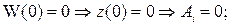
Поскольку 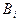не может равняться нулю, то

.

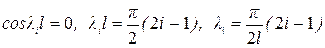Запишем выражение собственных форм колебаний:

.

Составим начальные условия. Для этого найдем выражение растянутой оси стержня при смещении правого конца на величину .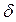

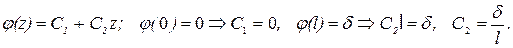
Окончательно

.

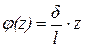Будем считать, что в начальный момент все точки оси стержня покоились, т. е. .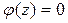

Запишем общее решение (7.5) в виде

.

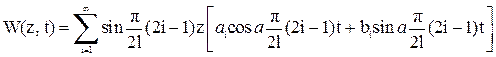Здесь коэффициенты 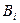учитываются постоянными 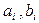. Начальные условия (7.6) приводят к соотношениям:

; .

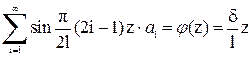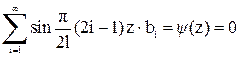Второе из этих начальных условий может быть выполнено при 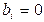, а для опре-деления коэффициентов 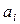воспользуемся свойством ортогональности собственных форм, т.е. условием

при 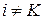. (7.7)

Умножим обе части соотношения 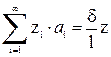на z_к и проинтегрируем по "z" в пределах от нуля до .

.

Из условия ортогональности собственных форм (7.7) следует, что все интегралы в левой части уравнения будут равны нулю при 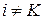, т.е. сумма будет содержать единственное слагаемое

.

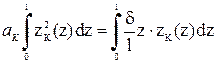Из этого выражения может быть получена формула для определения коэффи-циентов

.

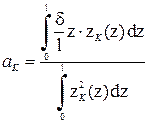Полученная формула вместе с выражением

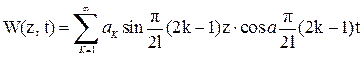
дает окончательное решение поставленной задачи.

Подсчитаем первый коэффициент 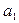и первую собственную частоту .

,

,

,

;

.

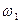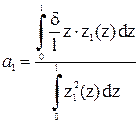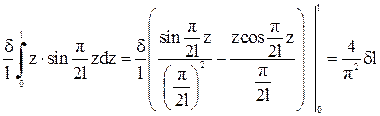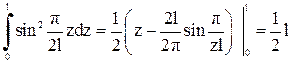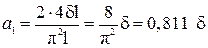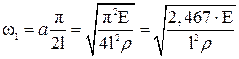В практических расчетах наибольший интерес представляет первая частота собственных колебаний , при которой, как правило, возникает резонанс. Эта частота может быть определена достаточно просто приближенным методом. Так, при продольных колебаниях стержня квадрат первой частоты может быть найден из выражения

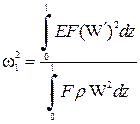, (7.8)

где - площадь поперечного сечения; - плотность материала стержня; - длина стержня.

Приближенность решения заключается в том, что в качестве функции 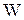выбирается любая функция, удовлетворяющая граничным условиям. Если же выбрать функцию, отвечающую форме колебаний данной системы, то получим точное решение.

Если стержень несет кроме распределенной и сосредоточенные массы, приложен-ные в сечениях 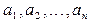(рис. 7.10), то формула квадрата частоты собственных колебаний примет вид

      Рис. 7.10 Стержень с сосредоточенными массами  

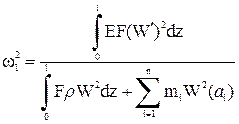. (7.9)

Определим 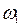для стержня (рис.7.9) при его продольных колебаниях. В качестве возьмем уравнение растянутой оси от равномерно приложенной нагрузки

(рис. 7.11).

;

; ; ;

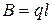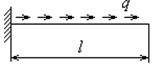    Рис. 7.11    

.

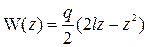Обозначим 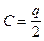, тогда .

Дата добавления: 2015-06-28