Подставив найденные величины в (7.10), получим

.

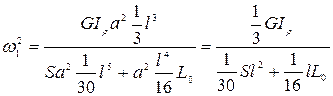Вычислив полярный момент инерции

,

найдем численное значение

.

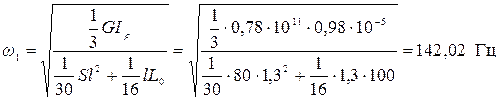Поперечные колебания

Точное решение задачи о поперечных колебаниях системы с распределенной массой может быть получено с помощью решения дифференциального уравнения

,

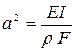
методом Фурье. Рассмотрим лишь приближенное определение первой собственной частоты колебаний .

При поперечных колебаниях стержня квадрат первой собственной частоты нахо­дится по формуле, аналогичной (7.9):

, (7.11)

где в качестве также используется любая функция, удовлетворяющая гранич-ным условиям. Формулу (7.11) называют формулой Рэлея, если V (z) принять в фор-ме, соответствующей статическому нагружению стержня.

    Рис. 7.14    

В качестве функции V (z) удобно брать первые слагаемые

рядов Тейлора или Фурье. Например, для балки (рис. 7.14)

построим функцию 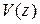в виде степенного и тригонометрического

полиномов.

Граничные условия для такого закрепления следующие:

1) 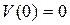, 2) , 3) , 4) .

Чтобы удовлетворялись четыре граничных условия,

возьмем четыре первых члена ряда Фурье:

, (7.12)

тогда

;

;

.

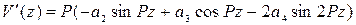Граничные условия приводят к следующей системе линейных уравнений:

(7.13)

Два последних уравнения (7.13) представляют систему двух однородных урав-нений, для решения которой необходимо, чтобы определитель, составленный из коэффициентов при , равнялся нулю.

,

.

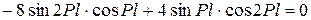После преобразования

.

Поскольку выражение в скобках не может равняться нулю, то

, и .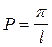

Тогда из третьего уравнения системы (7.13) следует, что , а из первого уравнения .

Обозначив , получим окончательное выражение

. (7.14)

Построим теперь V (z) в виде степенного полинома. Для этого возьмем

.

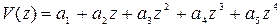Граничные условия приведут к системе уравнений:

Решая систему, находим, что , .

Обозначив , получим

.

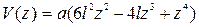Аналогично могут быть найдены коэффициенты для других граничных условий. Для некоторых часто встречающихся типов закрепления функции V (z) в тригонометрической и степенной формах приведены в табл. 7.1.

Необходимо отметить, что выражение (7.14), удовлетворяющее всем граничным условиям, довольно громоздко. Поэтому в расчетах используют более простые выражения, которые, однако, отвечают не всем граничным условиям. Эти выражения в табл. 7.1 помечены звездочкой. Использование этих функций незначительно снижает точность расчета частоты собственных колебаний.

Примеры решения задач

Задача 1

Схема колебательной системы показана на рис. 7.15. Исходные данные к задаче следующие: сосредоточенная масса 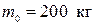, распределенная масса , длина стержня , поперечное сечение - двутавр № 18а, модуль упругости материала .

Таблица 7.1

Условия закрепления	Граничные условия	Функции V (z), l - длина стержня l
1)	, , , .
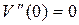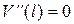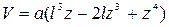
2)	, , , .
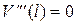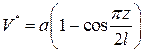
3)	, , , .
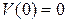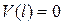4)	, , , .
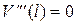5)	, , , .
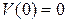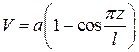
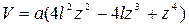
6)	, , , .

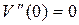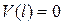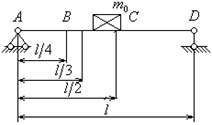    Рис. 7.15    

а) Определение частоты собственных колеба

ний без учета распределенной массы

Для определения частоты необходимо найти - перемещение от единичной силы в точке

.Рассмотрим расчетную схему (рис. 7.16).

Найдем ,

.

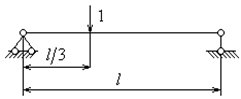    Рис. 7.16    

Граничные условия

1) 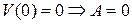, 2) ,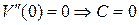

3) ,

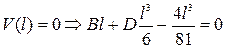4) .

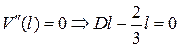Из третьего и четвертого граничных усло-

вий следует, что

; .

,

.

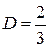Знак минус указывает только на направление перемещения, а в расчетах необхо-димо использовать абсолютную величину .

Из таблиц сортамента найдем .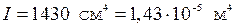

.

Проверим размерность .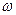

.

Ответ: .

б) Определение частоты собственных колебаний с учетом распределенной массы

Запишем формулу (7.11) с учетом того, что масса распределена на участках и 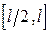и в точке приложена сосредоточенная масса .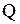

.

Выберем в качестве 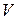тригонометрическое выражение (табл. 7.1)

,

тогда вторая производная примет вид

.

Вычислим интегралы, входящие в выражения :

;

;

;

.

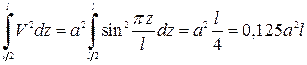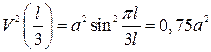Подсчитаем величину

.

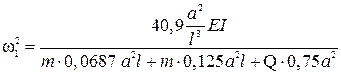Поделив на числитель и знаменатель, получим

;

.

Таким образом, учет распределенной массы дал некоторое снижение частоты колебаний.

Задача 2

Исходные данные: кг; кг/м; ; ; 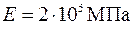поперечное сечение - двутавр №16.

а) Определение частоты собственных колебаний без учета распределенной массы

Найдем 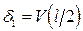при помощи интеграла Мора:

.

    Рис. 7.17    

Граничные условия:

1) ;

2) ;

, ;

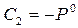      Рис. 7.18 Расчетная схема к определению    

;

.

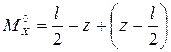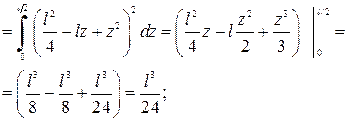
Из таблиц сортамента [19] найдем .

; .

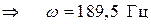б) Определение собственной частоты с учетом распределенной массы

Расположение точек , , 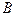, (рис. 7.17) означает, что на участке распределена погонная масса , а на участке . Запишем с учетом этого формулу Рэлея:

.

Из табл. 7.1 выберем в качестве функции V (z) степенной полином

.

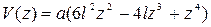Найдем вторую производную

.

Вычислим интегралы в формуле Рэлея:

;

;

;

.

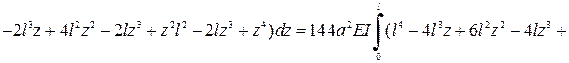
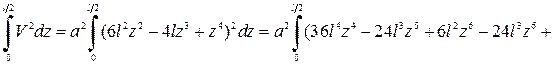
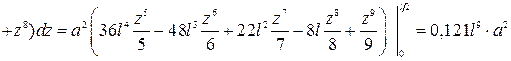Найдем

Поделив на числитель и знаменатель, получим

,

.

Подсчитаем эту же собственную частоту, используя функцию , удовлетворяющую не всем граничным условиям:

, ,

;

;

.

.

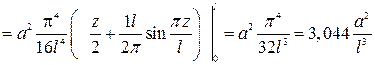После преобразования найдем

.

Таким образом, использование более простого выражения V (z) привело к незна-чительному изменению величины .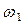

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Анурьев В.И. Справочник конструктора-машиностроителя. 7-е изд., перераб. и доп. М.: Машиностроение, 1992. Т.1. 816 с; Т.2. 784 с; Т.З. 720 с.

2. Беляев И.М. Сопротивление материалов.,М.: Наука, 1953. 856 с.

3. Белый В.Д., Карасев А.В., Соколовский З.Н. Расчёт деталей машин на прочность и жёсткость: Учеб. пособие / ОмПИ. Новосибирск: Изд. НИСИ, 1978. 83 с.

4. Белый В.Д. Стержни и стержневые системы: Учеб. пособие. Омск: Изд. ОмПИ, 1980. 92 с.

5. Белый В.Д., Карасев А.В., Соколовский З.Н. Расчет стержневых элементов машин и механизмов: Учеб. пособие. Омск: Изд. ОмПИ, 1980. 80 с.

6. Белый В.Д. Прочность и устойчивость стержневых систем: Учеб. пособие. Омск: Изд. ОмПИ, 1981. 72 с.

7. Белый В.Д. Напряжения и деформации в твердых телах: Учеб. пособие. Омск: Изд. ОмПИ, 1982. 84 с.

8. Белый В.Д. Поперечные колебания стержней: Учеб. пособие. Омск: Изд. ОмПИ, 1983.84 с.

9. Белый В.Д. Тонкостенные стержни: Учеб. пособие. Омск: Изд. ОмПИ, 1984. 82 с.

10. Белый В.Д. Пластины и оболочки: Учеб. пособие. Омск: Изд. ОмПИ, 1985. 100 с.

11. Белый В.Д. Напряжения и деформации в стержнях и стержневых системах: Учеб. пособие. Омск: Изд. ОмПИ, 1986. 103 с.

12. Бейзельман Р.Л., Ципкин Б.В., Перель Л.Д. Подшипники качения. М.:
Машиностроение, 1975. 605 с.

13. Зенкевич О. Метод конечных элементов в технике. М.: Наука, 1975. 314 с.

14. Общетехнический справочник / Под ред. Е.А. Скороходова. 2-е изд.,
перераб. и доп. М.: Машиностроение, 1982. 415 с.

15. Проектирование механических передач / С.А. Чернавский, Г.А. Снесарев,
Б.С.Козинков и др. 5-е изд., перераб. и доп. М.: Машиностроение, 1984. 560 с.

16. Путята Т.В., Можаровский Н.С., Соколов Н.Г. Прикладная механика.
Киев: Виша школа, 1985. 563 с.

17. Работнов Ю.Н. Механика деформируемого твёрдого тела. М.: Наука, 1979. 744 с.

18. Решетов Д.Н. Детали машин. М.: Машиностроение, 1975. 665 с.

19. Справочник по сопротивлению материалов / Под ред. Г.С. Писаренко. 2-е изд., перераб. и доп. Киев: Наук, думка, 1988. 736 с.

20. Тимошенко СП. Колебания в инженерном деле. М.: Гос. изд-во физ.-
матлит., 1959. 439 с.

21.Тимошенко СП. Сопротивление материалов. М.: Мир, 1965. 692 с. 22. Феодосьев В.И. Сопротивление материалов. М.: Наука, 1986. 512 с.

Добренко Александр Максимович

Сердюк Виталий Степанович

ИНЖЕНЕРНЫЕ РАСЧЕТЫ ПРИ ПРОЕКТИРОВАНИИ БЕЗОПАСНЫХ ТЕХНИЧЕСКИХ СИСТЕМ

Учебное пособие

Дата добавления: 2015-06-28