
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Расчет стержней на колебания
|
|
|
|
Процесс изменения параметра системы (координаты, деформации, напряжения и др.), который характеризуется многократным поочередным возрастанием и убыванием параметра во времени, называется колебательным процессом, а соответствующий параметр - колеблющейся величиной.
В зависимости от характера источника энергии различают колебания: собственные, вынужденные, параметрические и автоколебания.
Колебания, которые совершаются без поступления энергии извне, называются свободными или собственными колебаниями. В том случае, когда колебания вызываются переменным внешним воздействием, они называются вынужденными. Колебания называются параметрическими, если они вызываются изменением во времени параметров системы. Колебания, возникающие и поддерживающиеся от источника энергии неколебательной природы, называются автоколебаниями.
В зависимости от вида деформации упругих элементов различают продольные, поперечные и крутильные колебания (рис. 7.1).
По количеству степеней свободы различают колебательные системы с одной, несколькими и с бесконечным числом степеней свободы.
7.1. Колебания упругой системы с одной степенью свободы
Примером такой системы может служить невесомая система, содержащая одну материальную точку, положение которой определяется одним параметром - прогибом, углом поворота, осевым перемещением (рис. 7.1).
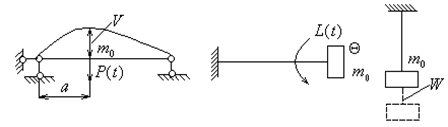
а) б) в)
Рис. 7.1 Колебательные системы с одной степенью свободы:
а - поперечные, б - крутильные,
в - продольные колебания
При поперечных колебаниях дифференциальное уравнение движения без учета затухания имеет вид

 V-ω2 V = f (t), (7.1)
V-ω2 V = f (t), (7.1)
где 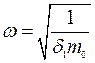 -угловая частота собственных колебаний,
-угловая частота собственных колебаний,  ,
,  - перемещение балки в точке
- перемещение балки в точке 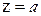 от единичной силы, статически приложенной в этом же сечении.
от единичной силы, статически приложенной в этом же сечении.
Решение уравнения (7.1) может быть получено методом Коши:
 , (7.2)
, (7.2)
где  и
и 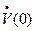 - перемещение и скорость в начальный момент времени
- перемещение и скорость в начальный момент времени 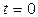 .
.
 Рис. 7.2 Рис. 7.2
|
Рассмотрим свободные колебания балки (рис. 7.2), вызванные мгновенным присоединением в точке  cсосредоточенной массы
cсосредоточенной массы 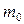 , имеющей первоначальную скорость
, имеющей первоначальную скорость 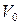 .
.
В этом случае переменное внешнее воздействие отсутствует, т.е.  , перемещение в начальный момент также равно нулю (V(0) = 0), а скорость
, перемещение в начальный момент также равно нулю (V(0) = 0), а скорость  . Тогда движение системы будет происходить по закону
. Тогда движение системы будет происходить по закону
 .
.
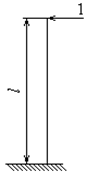 Рис. 7.3
Рис. 7.3
|
Для определения собственной частоты колебаний  необходимо приложить в точке
необходимо приложить в точке  единичную силу (рис.7.3) и найти перемещение
единичную силу (рис.7.3) и найти перемещение 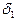 . Используем для этой цели интеграл
. Используем для этой цели интеграл
Мора [8]
 .
.
Необходимо отметить, что последнее слагаемое следует учитывать лишь в одной точке:  . Для определения
. Для определения 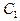 ,
, 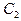 используем граничные условия
используем граничные условия

из которых найдем 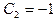 ,
,  .
.
Тогда
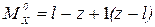 ,
,
а перемещение
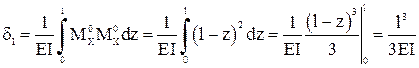 .
.
Окончательно получим выражение
 .
.
Таким образом, колебания будут совершаться по гармоническому закону с амплитудой 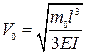 .
.
Рассмотрим вынужденные колебания шарнирно опертой балки (рис. 7.4) без учета затухания.
 Рис. 7.4
Рис. 7.4
|
Пусть  , поперечное сечение стержня – круг диаметром
, поперечное сечение стержня – круг диаметром  ,
, 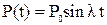 ,
, 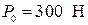 ,
,  частота возмущающей силы.
частота возмущающей силы.
Предположим, что в начальный момент времени балка покоилась, т.е.  и
и 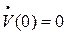 .
.
Тогда из (7.2) следует, что
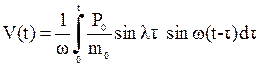 .
.
Преобразуем полученное выражение:


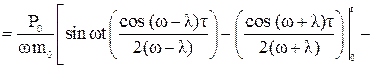
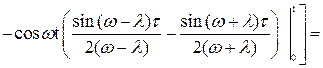
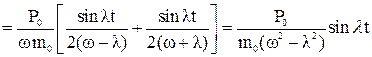 .
.
Необходимо обратить внимание на то, что найденное уравнение движения имеет смысл только при  .
.
 Рис. 7.5
Рис. 7.5
|
Определим собственную частоту колебаний  , используя интеграл Мора для вычисления
, используя интеграл Мора для вычисления  .
.

Найдем 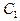 и
и 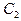 из граничных условий
из граничных условий
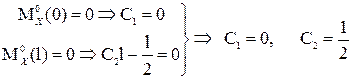 .
.
Определим

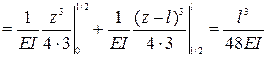 .
.
Для расчета частоты собственных колебаний необходимо вычислить осевой мо-мент инерции
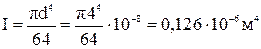 .
.
|
|
|
|
|
Дата добавления: 2015-06-28; Просмотров: 504; Нарушение авторских прав?; Мы поможем в написании вашей работы!