
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Примеры вычисления критической нагрузки приближенным методом
|
|
|
|
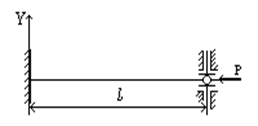
Задача 1
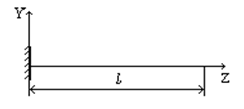
Защемленный левым концом стержень с постоянным поперечным сечением 6х12 см сжимается силой Р (рис. 6.18).
|
Таблица 6.4
| Схема закрепления концов стержня | Граничные условия | Рекомендуемые функции V(z) | ||
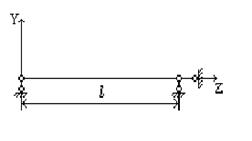 1 1
| ||||
| 1) |
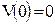 , ,  , ,  , , 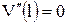 . .
|
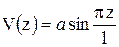 , ,
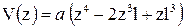
| ||
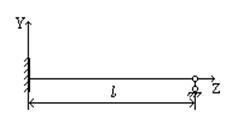 2) 2)
|
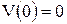 , ,  , , 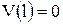 , , 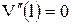 . .
|

| ||

|
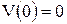 , ,  , , 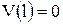 , , 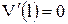 . .
|

| ||
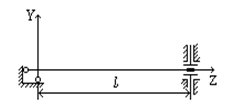 4) 4)
|
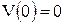 , ,  , ,  , , 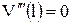 . .
|
 , ,

| ||
 5) 5)
| 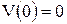 , , 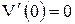 , ,  , , 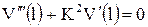 . .
| 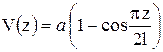 , ,

| ||
 6) 6) 
| 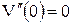 , , 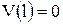 , ,

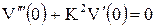
|  , ,
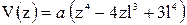
| ||
 7) 7)
| 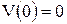 , ,  , ,

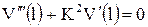 . .
| 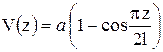 , ,
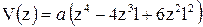
| ||
 Окончание табл. 6.4 Окончание табл. 6.4
| ||||
 8) 8)
| 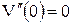 , , 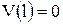 , ,
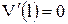 , , 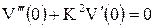 . .
|  , ,
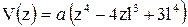
| ||
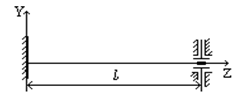 9) 9)
|
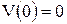 , , 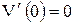 , , 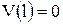 , ,  . .
|
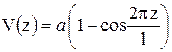 , ,
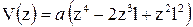
| ||
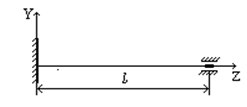 10) 10)
|
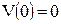 , , 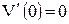 , ,  , ,  . .
|
 , ,
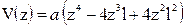
| ||
| 11) |
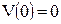 , ,  , ,  , ,  . .
|
 , ,
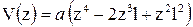
| ||
 12) 12)
|
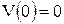 , , 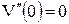 , ,
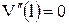
 . .
|
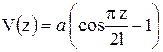 . .
| ||
Выберем функцию для изогнутой оси стержня в виде 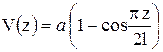 , запишем производные и проверим граничные условия:
, запишем производные и проверим граничные условия:
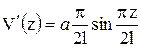 ;
;  ;
; 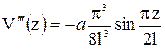 .
.
Граничные условия 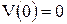 ,
,  ,
, 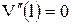 ,
, 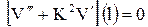 удовлетворяются. Следовательно, функция выбрана верно.
удовлетворяются. Следовательно, функция выбрана верно.
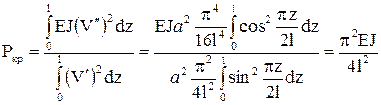 .
.
После подстановки исходных данных получим величину критической силы Ркр=1,07 МН.
Задача 2
 Стержень (рис. 6.19) сжимается силой Р.
Стержень (рис. 6.19) сжимается силой Р.
Определить критическую силу, если l=1 м и E=2.105 МПа. I=2.10-6 м4.
|
 . Производные функции
. Производные функции 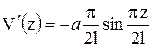 ;
;
 ;
; 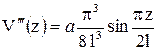 . Граничные условия
. Граничные условия 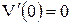 ,
, 
 и
и 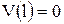 удовлетворяются.
удовлетворяются.
Вычислим критическую силу
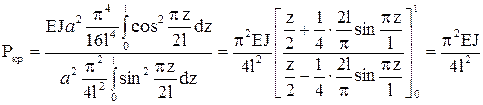 .
.
В результате подстановки исходных данных получим значение критической силы Ркр=1,03 MH.
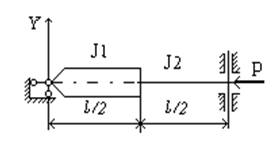 Задача 3
Задача 3
Определить силу Ркр и коэффициент приведения длины  для стержня (рис. 6.20). Вычисления сделать при следующих исходных данных:l=1,2м и E=2.105 МПа. J1=2J2 =1,9.10‑6 м4.
для стержня (рис. 6.20). Вычисления сделать при следующих исходных данных:l=1,2м и E=2.105 МПа. J1=2J2 =1,9.10‑6 м4.
|
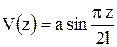 . Граничные условия удовлетворяются. Тогда
. Граничные условия удовлетворяются. Тогда
 .
.
Из этого выражения можно вычислить коэффициент приведения длины  .
.
 .
.
При подстановке исходных данных получим значение Ркр=0,5 МН.
Разберем несколько примеров, когда по длине стержня действуют осевые погонные нагрузки постоянной интенсивности q.
Задача 4
 Стержень (рис. 6.21) нагружен погонной нагрузкой постоянной интенсивности q. Определить критическую нагрузку
Стержень (рис. 6.21) нагружен погонной нагрузкой постоянной интенсивности q. Определить критическую нагрузку  , если l=3,5 м и E=2.105 МПа. J=3.10-6 м4.
, если l=3,5 м и E=2.105 МПа. J=3.10-6 м4.
Используя уравнение (6.26) и учитывая, что  , получаем выражение для критической
, получаем выражение для критической
|
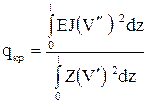 . (6.30)
. (6.30)
Уравнение формы изогнутой оси можно выбрать в виде полинома
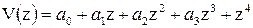 .
.
Запишем производные и из граничных условий найдем постоянные 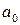 ,
,  ,
,
 и
и  :
:
 ;
;
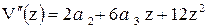 .
.
Граничные условия  и
и  дают значения
дают значения 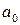 = 0 и
= 0 и  = 0. Граничные условия в защемленном конце
= 0. Граничные условия в защемленном конце 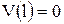 и
и 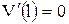 позволяют найти значения
позволяют найти значения  и
и 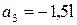 . Уравнение
. Уравнение 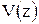 примет следующий вид:
примет следующий вид:
 ,
,
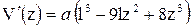 ,
,
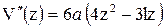 .
.
По формуле (6.30) определяем
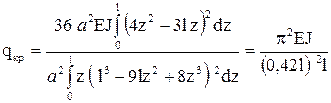 .
.
Таким образом, получим

Задача 5
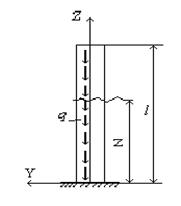
Определить критическую длину стальной стойки, на которую действует собственный вес (рис. 6.22), когда не теряется устойчивость.
Исходные данные: 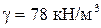 , E=2.105 МПа, F=6.10-2 м2, J=2.10‑4 м4.
, E=2.105 МПа, F=6.10-2 м2, J=2.10‑4 м4.
Вычислим 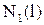 и подставим в уравнение (6.26)
и подставим в уравнение (6.26)
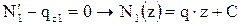
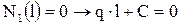 .
.
 Отсюда
Отсюда  . Тогда
. Тогда  .
.
 . (6.31)
. (6.31)
Решим задачу, используя несколько вариантов выбора формы изогнутой оси.
|
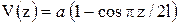 .
.
Определим первую и вторую производные:
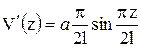 ,
,  .
.
Подставив производные в формулу (6.31), вычислим критическую нагрузку
 .
.
Коэффициент приведения длины  =1,1.
=1,1.
Теперь можно найти критическую длину стойки
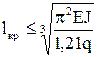 ,
,
где 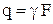 .
.
Подставив исходные данные, найдем, что 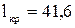 м.
м.
Вес стойки при этой длине 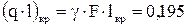 МН
МН
б) Выберем в качестве функции тригонометрический полином
 .
.
Найдем производные этого полинома и из граничных условий – коэффициенты a 0, a 1 и a 2:
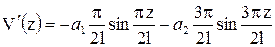 ;
;
 ;
;
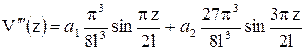 .
.
Граничные условия  ,
, 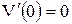 ,
, 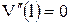 и
и  дают два уравнения:
дают два уравнения: 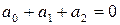 и
и 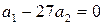 , откуда
, откуда 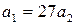 ,
,  .
.
Тогда уравнения будут следующими:
 ;
;
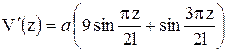 ;
;
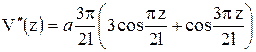 .
.
Вычислим критическую нагрузку
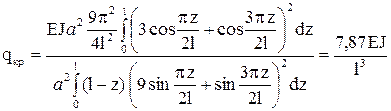 .
.
Критическая длина стойки
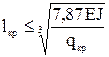 ,
, 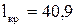 м.
м.
Вес стойки при этой длине  МН.
МН.
в) Выберем в качестве функции алгебраический полином пятой степени.
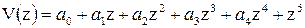 ;
;
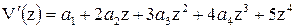 ;
;
 ;
;
 .
.
Используя граничные условия, находим коэффициенты полинома:
 ,
, 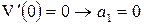 ,
,  ;
;
 ;
;
 .
.
Отсюда  . Тогда
. Тогда 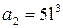 .
.
Получим полином и его производные по переменной “z” в следующем виде:
 ;
;
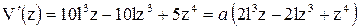 ;
;
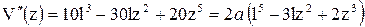 .
.
Вычислим критическую нагрузку и критическую длину стойки:
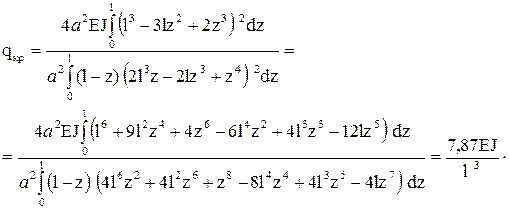
Подставив исходные данные, получим
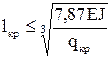 ,
, 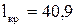 м.
м.
Вес стойки  МН.
МН.
Точное решение с использованием функций Бесселя получено в следующем виде  , откуда
, откуда 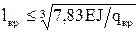 ,
,  м.
м.
Таким образом, все выбранные функции дают довольно близкие к точному решению значения, кроме функции 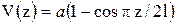 , так как эта функция не удовлетворяет граничному условию
, так как эта функция не удовлетворяет граничному условию  , поэтому получено завышенное значение на 1,7 % значение
, поэтому получено завышенное значение на 1,7 % значение 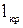 .
.
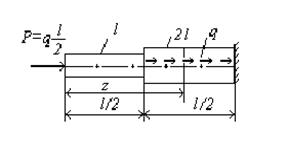
Задача 6
Для ступенчатого стержня переменного сечения, нагруженного в соответствии со схемой (рис. 6.23), определить критическую нагрузку и коэффициент приведения длины 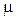 . Задачу решим двумя вариантами.
. Задачу решим двумя вариантами.
I вариант. Запишем уравнение изогнутой оси стержня: 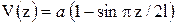 .
.
 Для вычисления критической нагрузки потребуются первая и вторая производные,
Для вычисления критической нагрузки потребуются первая и вторая производные,
а для проверки граничных условий - еще и третья. Запишем эти производные:
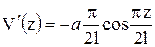 ;
; 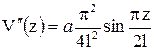 ;
;
|
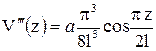 .
.
Значения функции и производных на концах стержня  ,
, 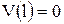 ,
, 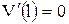 и
и 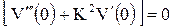 удовлетворяют граничным условиям.
удовлетворяют граничным условиям.
Запишем уравнение равновесия для деформированного стержня
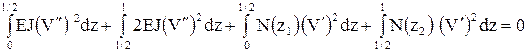 .
.
Уравнение продольных сил на первом и втором участках будут равны ( ,
, 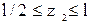 )
)
 и
и 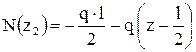 .
.
Получим

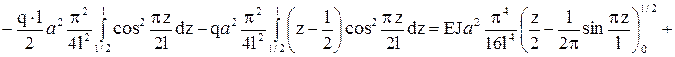


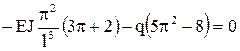 ,
,
 ,
,
где 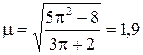 .
.
II вариант. Рассмотрим конструкцию как стержневую систему.
Для первого стержня  . Запишем первые три производные этого уравнения:
. Запишем первые три производные этого уравнения: 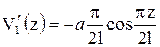 ;
; 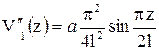 ;
; 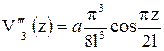 .
.
Для второго стержня  .
.
Первые три производные этого уравнения по переменной “z”
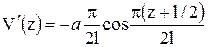 ;
;  ;
; 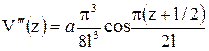 .
.
удовлетворяют всем граничным условиям:
1)  ; 2)
; 2)  ; 3)
; 3) 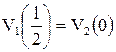 ;
;
4) 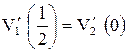 ; 5)
; 5) 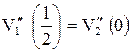 ; 6)
; 6) 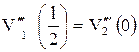 ;
;
7) 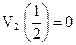 ; 8)
; 8) 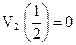 .
.
Для составления уравнений N1(z) и N2(z) рассмотрим стержневую систему (рис.6.24) и запишем уравнения

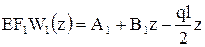 ,
, 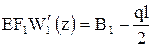 ,
,
 ,
, 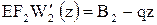 .
.
Из граничных условий и условий сопряжений находим
1)  ;
;
2)
|
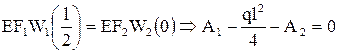 ;
;
3) 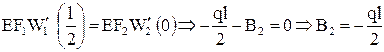 ;
;
4)  .
.
Тогда получим 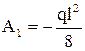 .
.
Теперь составим уравнения продольных сил для первого и второго участков
 ,
,  ;
;
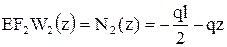 ,
,  .
.
Уравнение равновесия запишем в следующем виде:

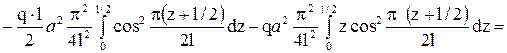
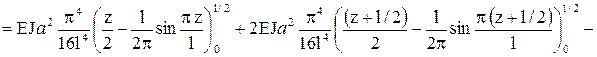

 ,
,
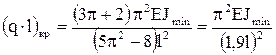 ,
,
где 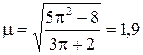 .
.
Если момент инерции сечения стержня  = 200 см4, l= 3 м и E = 2 105 MПа, получим
= 200 см4, l= 3 м и E = 2 105 MПа, получим
 .
.
Критическая нагрузка  =12 т.
=12 т.
Расчеты на устойчивость по коэффициенту снижения
основного допускаемого напряжения на сжатие
Ранее предполагалось, что в стержне при сжатии не возникают пластические деформации. Это предположение верно для тонких и длинных стержней, в которых напряжения сжатия при критических нагрузках остаются меньше предела пропорциональности. Для коротких стержней больших поперечных сечений критическая сила будет большей и в этом случае могут возникнуть пластические деформации еще до наступления потери устойчивости. Простой расчет на сжатие здесь не годится, так как стержень имеет достаточную длину и сохраняет особенности поведения, связанные с потерей устойчивости. С другой стороны, расчет на устойчивость по формуле Эйлера также не корректен, поскольку в стержне возникают пластические деформации. В этом случае расчет на устойчивость ведется по коэффициенту снижения основного допускаемого напряжения на сжатие. Этот метод заключается в том, что допускаемое напряжение на устойчивость 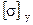 определяют как часть допускаемого напряжения на простое сжатие
определяют как часть допускаемого напряжения на простое сжатие  .
.
 , (6.32)
, (6.32)
где  - коэффициент снижения основного допускаемого напряжения на сжатие
- коэффициент снижения основного допускаемого напряжения на сжатие
(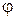 < 1).
< 1).
Допускаемые напряжения устойчивости и сжатия равны соответственно
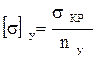 и
и 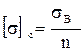 , (6.33)
, (6.33)
где  - критическое напряжение, определяемое по формуле Эйлера;
- критическое напряжение, определяемое по формуле Эйлера;  - предел прочности материала;
- предел прочности материала; 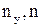 - коэффициенты запаса устойчивости и прочности.
- коэффициенты запаса устойчивости и прочности.
Таблица 6.5
| Гиб- кость | Значение коэффициента 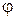
| ||||
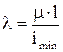
| Сталь Ст.2, Ст.3, 40С | Сталь Ст.5 | Чугун | Дерево (сосна, ель) | Сталь СПК |
| 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 0.99 | 0.98 | 0.97 | 0.99 | 0.97 | |
| 0.96 | 0.95 | 0.91 | 0.97 | 0.95 | |
| 0.94 | 0.92 | 0.81 | 0.93 | 0.91 | |
| 0.92 | 0.89 | 0.69 | 0.87 | 0.87 | |
| 0.89 | 0.86 | 0.57 | 0.80 | 0.83 | |
| 0.86 | 0.82 | 0.44 | 0.71 | 0.79 | |
| 0.79 | 0.76 | 0.34 | 0.60 | 0.72 | |
| 0.75 | 0.70 | 0.26 | 0.48 | 0.65 | |
| 0.69 | 0.62 | 0.20 | 0.38 | 0.55 | |
| 0.60 | 0.51 | 0.16 | 0.31 | 0.43 | |
| 0.52 | 0.43 | - | 0.25 | 0.35 | |
| 0.45 | 0.38 | - | 0.22 | 0.30 | |
| 0.40 | 0.32 | - | 0.18 | 0.26 | |
| 0.36 | 0.29 | - | 0.16 | 0.23 | |
| 0.32 | 0.26 | - | 0.14 | 0.21 | |
| 0.29 | 0.24 | - | 0.12 | 0.19 | |
| 0.26 | 0.21 | - | 0.11 | 0.17 | |
| 0.23 | 0.19 | - | 0.10 | 0.15 | |
| 0.21 | 0.17 | - | 0.09 | 0.14 | |
| 0.19 | 0.16 | - | 0.08 | 0.13 |
Коэффициент 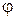 может быть выражен в виде
может быть выражен в виде
 . (6.34)
. (6.34)
Критические напряжения по формуле Эйлера будут равны
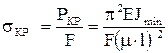 . (6.35)
. (6.35)
Введя в формулу (6.35) обозначения  (радиус инерции сечения) и
(радиус инерции сечения) и  (гибкость стержня) получим формулу Эйлера в следующем виде:
(гибкость стержня) получим формулу Эйлера в следующем виде:
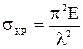 . (6.36)
. (6.36)
Критическое значение гибкости стержня определяется из условия 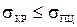 ,
,
где  - предел пропорциональности материала стержня.
- предел пропорциональности материала стержня.
Критическое значение гибкости получим
 . (6.37)
. (6.37)
Значения коэффициента снижения основного допускаемого напряжения в зависимости от материала и от гибкости стержня приведены в табл. 6.5.
Зная коэффициент снижения основного допускаемого напряжения на сжатие можно записать условие устойчивости:
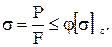
Пример расчета
Из условия устойчивости с использованием коэффициента снижения основного допускаемого напряжения 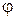 определить размеры прямоугольного сечения деревянной стойки, нагруженной продольной сжимающей силой Р.
определить размеры прямоугольного сечения деревянной стойки, нагруженной продольной сжимающей силой Р.
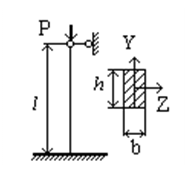 Схема закрепления концов стержня показана на рис. 6.25. Задачу решить при следующих исходных данных: отношение сторон прямоугольного сечения h:b=2:1; l=3м; P=200 кН;
Схема закрепления концов стержня показана на рис. 6.25. Задачу решить при следующих исходных данных: отношение сторон прямоугольного сечения h:b=2:1; l=3м; P=200 кН; 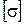 =10 МПа=1 кН/см2; Е=0,9 104 МПа.
=10 МПа=1 кН/см2; Е=0,9 104 МПа.
Выразим интегральные характеристики поперечного сечения и гибкость стойки через b:
|
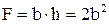 ,
, 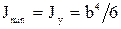 ,
, 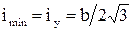 .
.
Тогда гибкость стойки
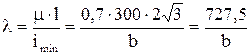 .
.
Необходимую величину сечения «b» найдем путем последовательных приближений.
В первом приближении принимаем 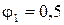 , тогда получим
, тогда получим
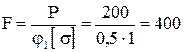 см2
см2 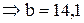 см.
см.
При этом гибкость стойки  .
.
Значение коэффициента  при
при 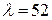 находим по табл. 6.5 путем интерполяции
находим по табл. 6.5 путем интерполяции
 .
.
Тогда допускаемое напряжение в поперечном сечении стойки

Действительное напряжение в сечении стойки:
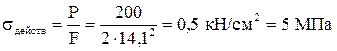 .
.
Сечение значительно недогружено: 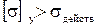 .
.
Возьмем следующее приближение:
 .
.
 и
и  .
.
Тогда гибкость стойки
 .
.
При гибкости стойки 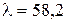
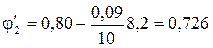 ,
,
 МПа,
МПа, 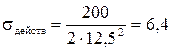 МПа.
МПа.
Сечение еще значительно недогружено.
Делаем третье приближение  , тогда необходимая площадь сечения
, тогда необходимая площадь сечения
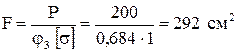 ,
, 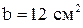 .
.
Гибкость стойки
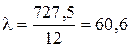 ,
, 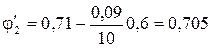 .
.
Допускаемое напряжение 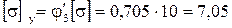 МПа.
МПа.
Действительное напряжение 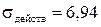 МПа.
МПа.
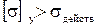 .
.
Недогрузка в этом случае составляет
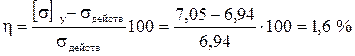 , что допустимо.
, что допустимо.
Таким образом, принимаем сечение с размерами b=12 см и h=24 см.
Значение критической силы
 .
.
Тогда коэффициент запаса устойчивости
 .
.
Для решения задач с использованием коэффициента снижения основного допустимого напряжения обычно достаточно трех-четырех приближений.
В прил. 6 приведены формулы для вычисления часто встречающихся интегралов при расчетах на устойчивость и дано индивидуальное задание по оценке силовых параметров при рассмотрении устойчивости стержней.
|
|
|
|
|
Дата добавления: 2015-06-28; Просмотров: 767; Нарушение авторских прав?; Мы поможем в написании вашей работы!