Вычислим интегралы в формуле для

определения :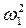

,

.

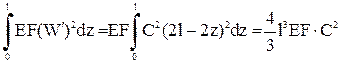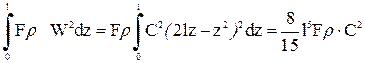Согласно (7.8) , .

Сравним найденное приближенное значение с точным. В точном решении коэффициент в числителе равен 2,467, а в приближенном 2,5. Это соответствует относительной ошибке, равной 0,42 %.

Найдем теперь эту же частоту, использовав в качестве 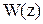уравнение растянутой оси стержня, соответствующее приложенной сосредоточенной силе на конце стержня (рис.7.12).

;

; ; .

    Рис. 7.12    

Учитывая, что 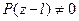только при z >l находим

.

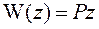Вычислим интеграл в формуле :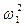

,

.

По (7.8)

, .

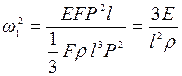В этом случае коэффициент в числителе подкоренного выражения равен трем, и относительная ошибка увеличилась до 6,54 %. Это объясняется тем, что функция 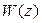удовлетворяла не всем граничным условиям, ее производная при терпела разрыв.

Использование в качестве уравнения оси стержня при статическом нагружении, соответствующем всем граничным условиям, было предложено Рэлеем.

Это приводит к наиболее точным результатам, однако иногда используют более простые выражения 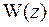, удовлетворяющие не всем граничным условиям, что значительно увеличивает погрешность расчетов.

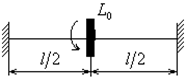    Рис. 7.13    

Найдем частоту крутильных колебаний стержня

(рис. 7.13).

Исходные данные: кг м² – сосредоточенный момент инерции; 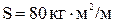- распределенный момент инерции; 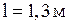; 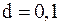м – диаметр поперечного сечения; 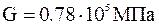(модуль сдвига).

Выражение для приближенного определения час-

тоты свободных крутильных колебаний может быть

записано в виде . (7.10)

Построим функцию - уравнения закрученной оси стержня при статическом нагружении.

;

; ; ;

.

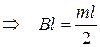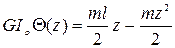Обозначив , получим .

Вычислим интегралы

,

,

.

Дата добавления: 2015-06-28