
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
В полярной системе координат 1 страница
КУРС
РАЗДЕЛ I. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
Определение: прямоугольной матрицей называется совокупность 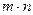 чисел, расположенных в виде прямоугольной таблицы, содержащей
чисел, расположенных в виде прямоугольной таблицы, содержащей 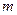 строк и
строк и  столбцов.
столбцов.
Обозначение: 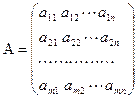
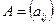 , где
, где 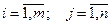
1.1. Основные действия над матрицами:
- Сложение:
если 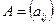 ,
, 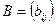 ,
, 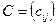 , где
, где 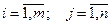 , то
, то 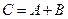 , а
, а  .
.
- Вычитание:
если 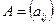 ,
, 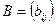 ,
, 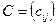 , где
, где 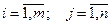 , то
, то 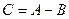 , а
, а  .
.
- Умножение матрицы на число:
если 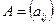 ,
, 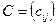 , где
, где 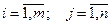 , то
, то  , когда
, когда 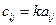 .
.
- Умножение матриц (возможно, когда число столбцов матрицы  равно числу строк матрицы
равно числу строк матрицы 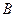 ):
):
Если 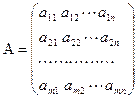 и
и  ,то С = АВ
,то С = АВ  , где
, где
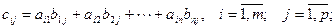
- транспонирование (замена строк матрицы соответствующими столбцами):
Если 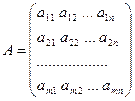 , то
, то 
1.2. Элементарные преобразования матриц:
- перестановка двух любых столбцов (строк);
- умножение столбца (строки) на число отличное от нуля;
- прибавление к столбцу (строке) линейной комбинации других столбцов (строк).
1.3. Вычисление определителей:
Вычисление определители второго порядка
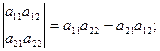
Вычисление определителей третьего порядка
а) по правилу треугольника
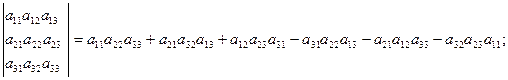
Символически правило треугольника можно записать так:
 |
б) разложение по элементам некоторого ряда, например:
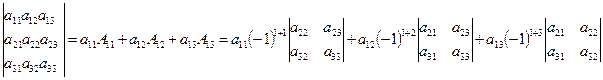
где 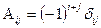 - алгебраическое дополнение элемента
- алгебраическое дополнение элемента 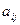 ;
;
 - минор элемента
- минор элемента 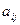 определителя
определителя 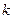 - го порядка ( определитель
- го порядка ( определитель  го порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент);
го порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент);
в) приведение к удобному виду, т.е. к такому определителю, у которого все элементы некоторого ряда, кроме одного, равны нулю (по свойству: величина определителя не изменится, если к элементам некоторого ряда прибавить соответствующие элементы параллельного ряда, предварительно умножив их на один и тот же множитель), а затем разложить определитель по элементам этого ряда, смотри выше.
1.4. Свойства определителей:
1. Величина определителя не изменится, если его транспонировать;
2. Перестановка двух любых параллельных рядов определителя равносильна его умножению на -1;
3. Если определитель имеет два одинаковых параллельных ряда, то он равен нулю;
4. Определитель равен сумме произведений элементов некоторого ряда на соответствующие им алгебраические дополнения;
5. Сумма произведений элементов какого-либо ряда на алгебраические дополнения элементов параллельного ряда равна нулю;
6. Если все элементы некоторого ряда содержат один и тот же множитель, то его можно вынести за знак определителя;
а) если все элементы некоторого ряда равны нулю, то сам определитель равен нулю;
б) если все элементы некоторого ряда пропорциональны соответствующим элементам параллельного ряда, то определитель равен нулю.
7. Если каждый элемент некоторого ряда определителя равен сумме двух слагаемых, то такой определитель можно представить в виде суммы двух определителей, из которых один в рассматриваемом ряду имеет первые слагаемые, а другой вторые. На остальных местах у всех трех определителей стоят одни и те же элементы;
8. Величина определителя не изменится, если к элементам некоторого ряда прибавить соответствующие элементы параллельного ряда, предварительно умножив их на один и тот же множитель;
1.5. Обратная матрица:
Определение: матрица  называется обратной квадратной матрице
называется обратной квадратной матрице  , если она, будучи умноженной как слева, так и справа на данную матрицу
, если она, будучи умноженной как слева, так и справа на данную матрицу  , дает соответствующую единичную, т.е.
, дает соответствующую единичную, т.е. 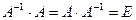 .
.
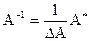 - формула нахождения обратной матрицы (
- формула нахождения обратной матрицы (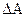 -определитель,
-определитель,  - союзная матрица, составленная из алгебраических дополнений квадратной матрицы
- союзная матрица, составленная из алгебраических дополнений квадратной матрицы  с последующим транспонированием);
с последующим транспонированием);
1.6.Свойства обратной матрицы:
- 
1.7. Формулы Крамера:
Пусть имеем систему  линейных уравнений с
линейных уравнений с  неизвестными:
неизвестными: 

 и пусть
и пусть 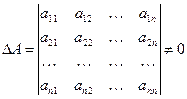 .
.
Система имеет единственное решение, которое можно найти по формулам Крамера:
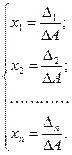 , где
, где 
 , ……,
, ……, 

Эту систему также можно решить другим способом, т.е., если записать эту систему в матричной форме 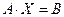 , то матричная форма решения системы
, то матричная форма решения системы 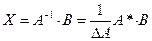 .
.
1.8. Теорема о числе решений совместных систем:
Определение: наивысший порядок ненулевого минора матрицы  называется ее рангом и обозначается
называется ее рангом и обозначается 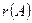 или
или 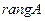 .
.
Определение: система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг основной матрицы  системы равен рангу расширенной
системы равен рангу расширенной  . Для системы
. Для системы 
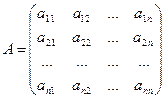 ,
, 
Пусть имеем совместную систему линейных уравнений
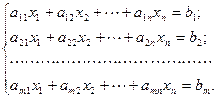
Так эта система совместна, то 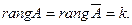 - ранг совместной системы.
- ранг совместной системы.
Теорема.
1. Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение.
2. Если ранг совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений.
Алгоритм решения совместных систем:
1) Пусть ранг совместной системы равен числу неизвестных и равен числу уравнений 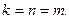 В этом случае единственное решение находят по формулам Крамера или матричным способом.
В этом случае единственное решение находят по формулам Крамера или матричным способом.
2) Пусть ранг совместной системы равен числу неизвестных, но меньше числа уравнений  В этом случае необходимо в системе оставить лишь те уравнения, коэффициенты которых составляют базисный минор матрицы
В этом случае необходимо в системе оставить лишь те уравнения, коэффициенты которых составляют базисный минор матрицы  системы, а затем искать единственное решение либо по формулам Крамера, либо матричным способом.
системы, а затем искать единственное решение либо по формулам Крамера, либо матричным способом.
3) Пусть ранг совместной системы меньше числа неизвестных, 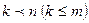 , тогда:
, тогда:
- в заданной системе выбираем  уравнений, из коэффициентов которых составлен базисный минор матрицы
уравнений, из коэффициентов которых составлен базисный минор матрицы  , а остальные уравнения отбрасываем;
, а остальные уравнения отбрасываем;
- неизвестные, коэффициенты при которых входят в базисный минор, так называемые главные неизвестные, оставляем в левой части системы, а остальные неизвестные, называемые свободными, переносим в правую часть;
- по формулам Крамера находим выражение главных неизвестных через свободные, полученные равенства представляют собой общее решение системы;
- придавая в общем решении свободным неизвестным конкретные числовые значения, находим конкретные числовые значения главных неизвестных. Совокупность числовых значений и главных, и свободных неизвестных дает определенное частное решение системы.
1.9. Метод Гаусса:
Суть метода состоит в том, что посредством последовательного исключения неизвестных заданная система
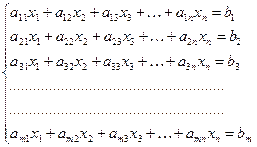 , у которой
, у которой 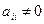 и
и 
преобразуется в ступенчатую (в частности, треугольную)
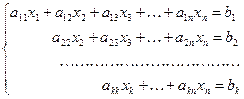
Замечания:
1) Метод Гаусса применим тогда и только тогда, когда все главные элементы  .
.
2) В процессе приведения заданной системы к ступенчатому виду могут получаться уравнения вида  , которые можно отбрасывать.
, которые можно отбрасывать.
3) При решении СЛАУ методом Гаусса удобнее приводить к ступенчатому виду расширенную матрицу этой системы, выполняя преобразования над ее строками.
1.10.Однородные системы линейных уравнений:
Определение: систему линейных уравнений называют однородной, если все ее свободные члены равны нулю.
Теорема:
Однородная система линейных уравнений имеет нетривиальное (ненулевое) решение тогда и только тогда, когда ранг системы меньше числа неизвестных.
Следствие:
Любая однородная система линейных уравнений, в которой число уравнений меньше числа неизвестных, имеет хотя бы одно нетривиальное решение.
Теорема:
Однородная система линейных уравнений, в которой число уравнений равно числу неизвестных, имеет нетривиальное решение тогда и только тогда, когда определитель системы равен нулю.
 - однородная система двух уравнений с тремя неизвестными.
- однородная система двух уравнений с тремя неизвестными.

Ответ: 
РАЗДЕЛ II. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
2.1. Основные понятия:
Определение: вектором называется направленный прямолинейный отрезок, т.е. отрезок, имеющий определенную длину и направление.
Определение: два ненулевыхвектора называются ортогональными, если угол между ними равен 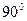 . Обозначение:
. Обозначение:  .
.

Определение: два ненулевых вектора называются коллинеарными, если они лежат на одной или параллельных прямых. Обозначение: 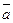 ║
║  .
.
 - сонаправленные вектора.
- сонаправленные вектора.
 - противоположнонаправленные вектора.
- противоположнонаправленные вектора.
Определение: два вектора равны тогда и только тогда, когда их длины равны и они сонаправлены.

Определение: три ненулевых вектора называются компланарными, если они лежат в одной или параллельных плоскостях.
Определение: если начало и конец вектора совпадают, то он называется нулевым  , его длина равна нулю.
, его длина равна нулю.
Вектор, длина которого равна единице, называется единичным.
- Если 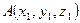 - начало вектора,
- начало вектора,  - конец вектора, то
- конец вектора, то
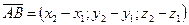 ;
;
- 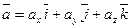 - разложение вектора по ортам координатных осей, где
- разложение вектора по ортам координатных осей, где
 - координаты вектора
- координаты вектора
- Если 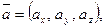 то
то 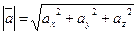 - длина вектора
- длина вектора
-  - направляющие косинусы вектора
- направляющие косинусы вектора 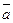 , где
, где 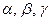 - углы, образованные вектором
- углы, образованные вектором 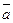 и координатными осями
и координатными осями  соответственно,
соответственно,  .
.
-
 Определение: единичный вектор, сонаправленный с вектором
Определение: единичный вектор, сонаправленный с вектором 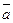 называется его ортом.
называется его ортом.
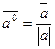 - орт вектора
- орт вектора 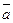
2.2. Линейные операции над векторами:
1) Определение: суммой нескольких векторов 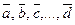 называется вектор
называется вектор  , соединяющий начало первого с концом последнего, если заданные векторы расположены так, что конец предыдущего является началом последующего.
, соединяющий начало первого с концом последнего, если заданные векторы расположены так, что конец предыдущего является началом последующего.

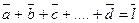
2) Определение: разностью двух векторов 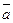 и
и  называется третий вектор
называется третий вектор  который, будучи сложенным с вектором
который, будучи сложенным с вектором  дает вектор
дает вектор 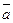 .
.
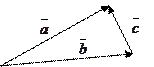
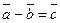
3) Определение: произведением вектора  на скаляр
на скаляр 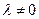 называется вектор, который имеет длину, равную
называется вектор, который имеет длину, равную  и сонаправлен с
и сонаправлен с 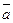 , если
, если  , противоположно направлен, если
, противоположно направлен, если  .
.

2.3. Скалярное произведение векторов:
Определение: скалярным произведением двух ненулевых векторов называется число, равное произведению длин этих векторов на косинус угла между ними: 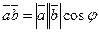

Определение: проекцией вектора 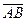 на ось
на ось  называется длина вектора
называется длина вектора  оси, соединяющего проекции начала и конца вектора, взятая со знаком плюс, если отрезок оси сонаправлен с осью и со знаком минус, если противоположно направлен
оси, соединяющего проекции начала и конца вектора, взятая со знаком плюс, если отрезок оси сонаправлен с осью и со знаком минус, если противоположно направлен 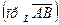
Так же, скалярное произведение можно найти, используя формулу: 
Свойства:
1) 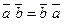 - перестановочное;
- перестановочное;
2) 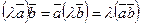 - сочетательное;
- сочетательное;
 3)
3)  - распределительное;
- распределительное;
4) 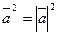 - квадрат вектора равен квадрату его длины;
- квадрат вектора равен квадрату его длины;
5) 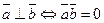 - условие ортогональности векторов.
- условие ортогональности векторов.
Приложения:
1)  - условие ортогональности векторов
- условие ортогональности векторов
 и
и 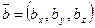
2) 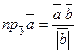 ;
; 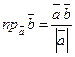 - проекция одного вектора на направление другого.
- проекция одного вектора на направление другого.
3) 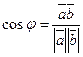 - косинус угла между векторами
- косинус угла между векторами  и
и 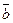 .
.
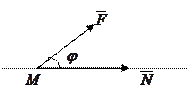 4) Если материальная точка перемещается прямолинейно из положения
4) Если материальная точка перемещается прямолинейно из положения  в положение
в положение  под действием силы
под действием силы  , составляющей угол
, составляющей угол  с направлением перемещения, то работа этой силы:
с направлением перемещения, то работа этой силы: 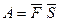 .
.
2.4. Векторное произведение векторов:
Определение: некомпланарные вектора  и
и  , взятые в указанном порядке, образуют правую тройку, если кратчайший поворот от первого
, взятые в указанном порядке, образуют правую тройку, если кратчайший поворот от первого  вектора до совмещения со вторым вектором
вектора до совмещения со вторым вектором  виден с конца третьего вектора
виден с конца третьего вектора  совершающимся против часовой стрелки, и левую, если по часовой.
совершающимся против часовой стрелки, и левую, если по часовой.
 |
 Определение:
Определение:
Векторным произведением двух ненулевых векторов, называется третий вектор  , который удовлетворяет условиям:
, который удовлетворяет условиям:
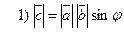 ;
;
2) 
3)  .
.
Формула нахождения векторного произведения векторов  и
и 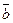 ,
,
если  и
и 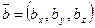 :
: 
Свойства:
1) 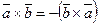 - антиперестановочное;
- антиперестановочное;
2) 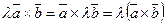 - сочетательное;
- сочетательное; 
3)  - распределительное;
- распределительное;
4)  ║
║ 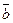
 - условие коллинеарности векторов.
- условие коллинеарности векторов.
Приложения:
1)  ║
║ 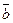

 или
или  - условие коллинеарности векторов
- условие коллинеарности векторов  и
и 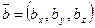 .
.
2) Формулы нахождения площадей:
 - для треугольника
- для треугольника
 - для параллелограмма, построенного на этих векторах, как на сторонах.
- для параллелограмма, построенного на этих векторах, как на сторонах.
3)

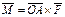 - момент силы
- момент силы  , приложенной в точке
, приложенной в точке 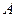 ,
,
относительно точки О.
4)
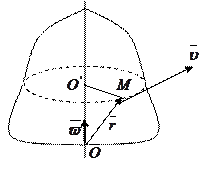 Если М – произвольная точка твердого тела, вращающегося вокруг неподвижной оси с постоянной угловой скоростью, то линейная скорость этой точки:
Если М – произвольная точка твердого тела, вращающегося вокруг неподвижной оси с постоянной угловой скоростью, то линейная скорость этой точки: 
(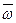 - угловая скорость,
- угловая скорость, 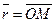 ).
).
|
|
Дата добавления: 2015-06-28; Просмотров: 414; Нарушение авторских прав?; Мы поможем в написании вашей работы!