КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
В полярной системе координат 3 страница
|
|
|
|
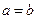 - однополостный гиперболоид вращения)
- однополостный гиперболоид вращения)
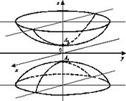
2. 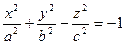 - двуполостный гиперболоид (если
- двуполостный гиперболоид (если 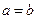 - двуполостный гиперболоид вращения)
- двуполостный гиперболоид вращения)
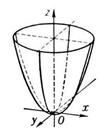
3. 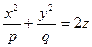 - эллиптический параболоид (если
- эллиптический параболоид (если
 - параболоид вращения)
- параболоид вращения)
|
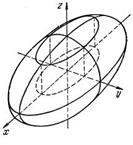
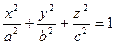 - трехосный эллипсоид
- трехосный эллипсоид
(если  - сфера)
- сфера)

5.  - конус второго порядка
- конус второго порядка

6. 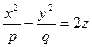 - гиперболический параболоид
- гиперболический параболоид
РАЗДЕЛ V. ГРАФИКИ ОСНОВНЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
1. 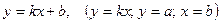 - прямая
- прямая
 | |||
 | |||
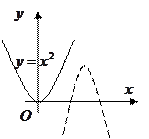
2. 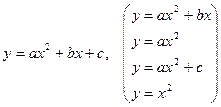 - парабола
- парабола

3. 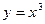 - кубическая парабола
- кубическая парабола
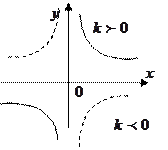
4.  - гипербола
- гипербола

5. 

6. 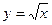

7. 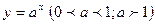 - показательная функция
- показательная функция


8.  - степенная функция 9.
- степенная функция 9. 

10. Логарифмические
функции:
 -
-
11. Тригонометрические функции:
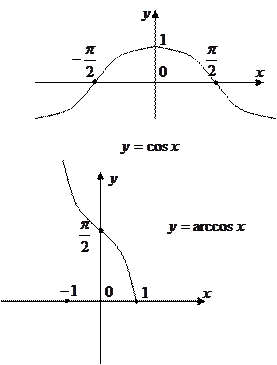 | |||||
 | |||||
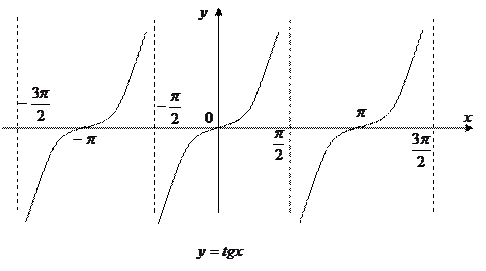 |

РАЗДЕЛ VI. УРАВНЕНИЯ И ГРАФИКИ КРИВЫХ
1. Окружности:
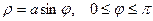
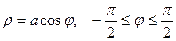
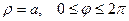
 |  |  |
2. Кардиоиды:
 | 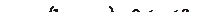 |
3. Розы: 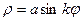 ;
; 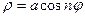 .
.
При четном  - число лепестков удваивается, при нечетном - число лепестков совпадает с
- число лепестков удваивается, при нечетном - число лепестков совпадает с  .
.
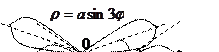 | |||
 | |||
4. Лемниската Бернулли: 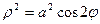
5. Спирали:

 - спираль Архимеда
- спираль Архимеда 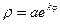 - логарифмическая спираль
- логарифмическая спираль
РАЗДЕЛ VII. КРИВЫЕ, ЗАДАННЫЕ ПАРАМЕТРИЧЕСКИ
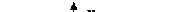
1. Окружность:
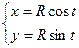 , где
, где 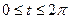 .
.

2. Эллипс:
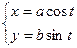 , где
, где 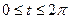 .
.
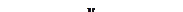
3. Астроида:
 , где
, где 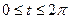 .
.
 4. Циклоида:
4. Циклоида:
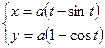 ,
, 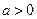
для первой арки 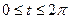 .
.
РАЗДЕЛ VIII. НАХОЖДЕНИЕ ПРЕДЕЛОВ
8.1. Определение пределов:
Определение 1: число 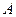 называется пределом функции
называется пределом функции  в точке
в точке 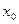 , если для любого положительного
, если для любого положительного  найдется такое положительное
найдется такое положительное 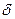 , что для всех
, что для всех 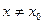 , удовлетворяющих неравенству
, удовлетворяющих неравенству 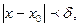 выполняется неравенство
выполняется неравенство 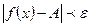
Символически:
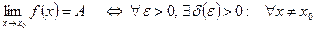 и
и 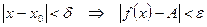

Геометрический смысл: если для 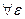 - окрестности т.
- окрестности т. 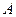 найдется
найдется 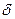 - окрестность
- окрестность 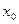 , что для всех
, что для всех 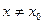 из этой
из этой 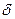 - окрестности соответствующие значения функции
- окрестности соответствующие значения функции  лежат внутри полосы шириной
лежат внутри полосы шириной  , ограниченной прямыми
, ограниченной прямыми 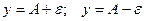 .
.
Суть понятия предела: 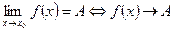 при
при 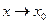
Определение 2: число 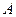 называется пределом функции
называется пределом функции  при
при 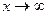 , если для любого
, если для любого 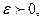 существует
существует 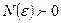 , что при всех
, что при всех 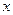 , удовлетворяющих неравенству
, удовлетворяющих неравенству  , справедливо неравенство
, справедливо неравенство
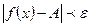 .
.
Обозначение:  .
.

Геометрический смысл: если существует  , то для всякого сколь угодно малого наперед заданного числа
, то для всякого сколь угодно малого наперед заданного числа  найдется такое свое число
найдется такое свое число 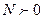 ,
,  , что, как только становится
, что, как только становится 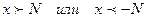 , соответствующие значения функции попадают в
, соответствующие значения функции попадают в  полосу числа
полосу числа 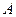 .
.
Суть понятия: 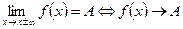 при
при 
8.2. БМФ и ББФ, непрерывность функции:
Определение: функция  называется бесконечно малой (бмф), если
называется бесконечно малой (бмф), если  (
(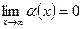 ).
).
Теорема: Сумма конечного числа бесконечно малых функции в т. 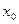 есть функция бесконечно малая.
есть функция бесконечно малая.
Теорема: Произведение бмф на ограниченную (она ограничена в сколь угодно малой окрестности точки) есть функция бесконечно малая.
Следствия:
1) Произведение постоянной на бмф есть бмф;
2) Произведение двух бмф есть бмф;
3) Частное от деления бмф на функцию, имеющую предел, отличный от нуля, есть бмф.
Аналогично, если:
Если 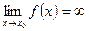
 , то
, то  - бесконечно большая функция (ббф).
- бесконечно большая функция (ббф).
Свойства ббф:
1) Произведение ббф на функцию, имеющую предел, отличный от нуля, есть ббф;
2) Произведение двух ббф есть ббф;
3) Сумма и частное двух ббф есть ббф не всегда.
Теорема: Если  - ббф в т.
- ббф в т. 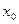 , то
, то 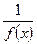 - бмф в т.
- бмф в т. 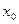 .
.
Теорема: Если 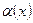 - бмф в т.
- бмф в т. 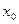 , то
, то 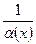 - ббф в т.
- ббф в т. 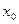 .
.
Теоремы о пределах:
Теорема 1: Если две функции имеют предел, то их сумма также имеет предел, равный сумме пределов этих функций
Теорема 2: Если две функции имеют предел, то их произведение также имеет предел, равный произведению пределов этих функций
Теорема 3: Если две функции имеют предел, то их частное имеет предел, равный частному пределов этих функций, при условии, что предел делителя отличен от нуля.
Следствия:
1) Постоянный множитель можно выносить за знак предела.
2) Теоремы 1 и 2 остаются справедливыми и в случае любого конечного числа функции, имеющих предел.
Определение 1:
Функция  называется непрерывной в точке
называется непрерывной в точке 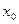 , если
, если 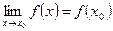 .
.
Определение 2:
Функция  называется непрерывной на множестве
называется непрерывной на множестве 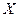 , если она непрерывна в каждой точке этого множества.
, если она непрерывна в каждой точке этого множества.
Из определений непрерывных функций следует:
1. 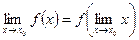 и
и 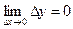 , где
, где 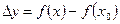 , а
, а 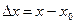 .
.
Каждая из основных элементарных функций непрерывна в своей области определения.
8.3. Алгоритм нахождения пределов:
1. Если функция  непрерывна в окрестности точки
непрерывна в окрестности точки 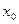 , то
, то 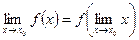 , т.е. для нахождения предела
, т.е. для нахождения предела 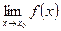 нужно вычислить значение этой функции в точке
нужно вычислить значение этой функции в точке 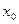 .
.
2. Если  - многочлен
- многочлен 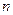 - ой степени, то:
- ой степени, то:
 ,
,
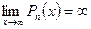 .
.
3. Если  - многочлен
- многочлен 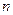 - ой степени,
- ой степени, 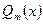 - многочлен
- многочлен 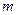 - степени, то
- степени, то
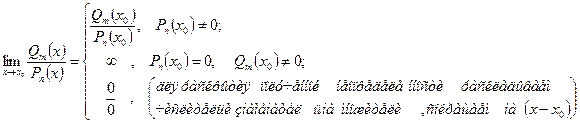
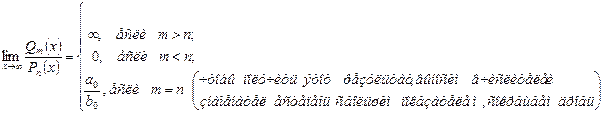
4. Если  - дробь, содержащая иррациональность, то
- дробь, содержащая иррациональность, то

8.4. Замечательные пределы:
1) 
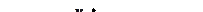 Теорема:
Теорема:
Предел отношения синуса к его аргументу равен 1, если аргумент стремится к нулю, т.е. 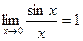 (первый замечательный предел).
(первый замечательный предел).
2) 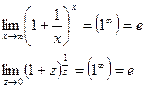 - второй замечательный предел.
- второй замечательный предел.
Следствие:  и
и  .
.
8.5. Нахождение пределов с использованием бесконечно малых функций (бмф):
Пусть  - бмф.
- бмф.
Сравнить две бмф, значит найти предел их отношения, т.е. 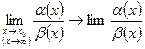 .
.
Определение: если 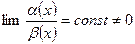 , то
, то 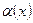 и
и  называются бмф одного порядка малости.
называются бмф одного порядка малости.
Определение: если  , то
, то 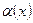 называют более высокого порядка малости, чем
называют более высокого порядка малости, чем  .
.
Символически: 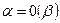 .
.
Определение: если 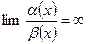 , то
, то 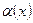 называют более низкого порядка малости по отношению к
называют более низкого порядка малости по отношению к  .
.
Определение: если 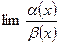 не существует, ни конечный, ни бесконечный, то
не существует, ни конечный, ни бесконечный, то 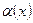 и
и  называют несравнимыми бмф.
называют несравнимыми бмф.
Определение: если 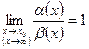 , то
, то 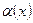 и
и  называются эквивалентными.
называются эквивалентными.
Символически: 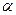 ~
~ 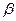
Таблица эквивалентных бмф при  :
:
1) 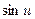 ~
~ 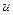 5)
5) 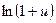 ~
~ 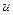 7)
7) 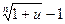 ~
~ 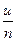
2) 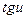 ~
~ 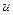
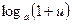 ~
~  8)
8)  ~
~ 
3) 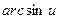 ~
~ 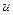 6)
6)  ~
~ 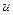
4) 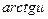 ~
~ 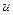
 ~
~ 
|
|
|
|
|
Дата добавления: 2015-06-28; Просмотров: 417; Нарушение авторских прав?; Мы поможем в написании вашей работы!