Уравнения первого порядка 2 страница

Например, если такая прямая параллельна оси , то уравнение : и .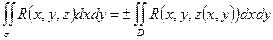

- формула Остроградского-Гаусса.

- формула Стокса.

РАЗДЕЛ I. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ

1.1. Основные понятия:

Определение: уравнение, содержащее неизвестные функции, их аргументы и производные (дифференциалы) различных порядков от этих функции по своим аргументам называется дифференциальным (д.у.).

Определение: порядком д.у. называется порядок старшей производной или старшего дифференциала функции, входящих в уравнение.

Определение: решением д.у. называется всякая функция, обращающая это уравнение в тождество.

Теорема Коши (существования и единственности решения д.у. первого порядка):

Если в д.у. первого порядка правая часть 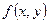и ее частная производная непрерывны в некоторой области 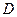плоскости 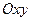, содержащей точку , то существует и притом единственное решение этого уравнения, удовлетворяющее условию .

Задача Коши:

Найти общее решение д.у. и, используя заданные начальные условия 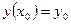, выделить из общего искомое частное решение.

1.2. Типы дифференциальных уравнений первого порядка:

1) С разделяющимися переменными:

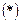- разрешенное относительно производной.

Алгоритм решения:

- заменяем в уравнении 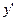на ;

- разделяем в уравнении переменные;

- интегрируем левую и правую части уравнения с разделенными переменными;

- записываем общее решение или общий интеграл.

Частный случай : ; ; .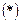

- д.у. с разделяющимися переменными в дифференциальной форме. Метод решения тотже.

2) Однородные дифференциальные уравнения:

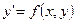, где - разрешенное относительно производной.

Ход решения:

- вводим новую функцию или ;

- сводим к уравнению с разделяющимися переменными, интегрируем.

(где - однородные функции одного измерения) – дифференциальная форма.

3) Линейные дифференциальные уравнения:

Общая форма: , где - непрерывные функции, в частности постоянные.

Признак: входят только в первой положительной степени и нет их произведения 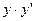; 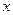- в любой форме.

Ход решения:

- подставляем в данное уравнение .

- решаем последовательно два д.у. с разделяющимися переменными: одно д.у. относительно 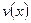, другое относительно ;

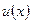- записываем общее решение (общий интеграл).

Еще одна форма линейного дифференциального уравнения: .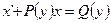

Решается введением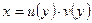

4) Уравнения Бернулли:

Общий вид - , где - любой действительное число , - непрерывные функции, в частности постоянные.

Эти уравнения сводят к линейным, поэтому решение .

5) Дифференциальные уравнения в полных дифференциалах:

, где .

Решение ищем в виде , где и - из области непрерывности .

1.3. Дифференциальные уравнения высших порядков:

Теорема Коши (существования и единственности решения д.у. второго порядка):

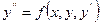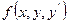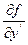Если в д.у. второго порядка правая часть и ее частные производные и непрерывны в некоторой области ,

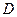содержащей значения , то существует и притом единственное решение этого уравнения, удовлетворяющее условию ,

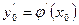
1) Дифференциальные уравнения вида , где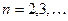

Для нахождения решения последовательно интегрируем заданное д.у. по 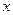столько раз, каков порядок уравнения.

2) Дифференциальные уравнения вида .

Для нахождения решения вводим новую функцию , тогда .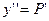

Замечание:

- д.у. вида , где 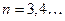решаем с помощью подставки .

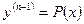3) Дифференциальные уравнения вида .

Для нахождения решения вводим новую функцию , тогда .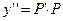

4) Линейное однородное дифференциальное уравнения - го порядка

(ЛОДУ).

Общий вид: , где и - заданные непрерывные функции, в частности константы

Определение:

Два частных решения и 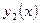ЛОДУ второго порядка образуют фундаментальную систему (ФСР) этого уравнения в 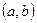, если ни в одной точке этого промежутка определитель Вронского 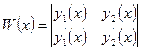не обращается в нуль.

Теорема (о структуре общего решения ЛОДУ второго порядка):

Если функции и 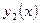образуют ФСР ЛОДУ второго порядка, то общее решение этого уравнения имеет вид 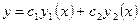, где и - произвольные постоянные.

Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами (ЛОДУ)

Общий вид: .

Ход решения:

- составляем характеристическое уравнение вида ;

- решаем характеристическое равнение, используя дискриминант;

- записываем общее решение, учитывая:

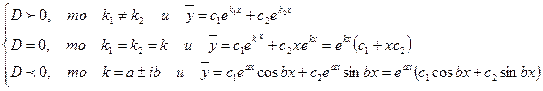
ЛОДУ высших порядков решаются аналогично.

5) Линейные неоднородные дифференциальные уравнения -го порядка (ЛНДУ).

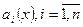Общий вид: , где и 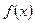- заданные непрерывные функции, в частности константы.

Теорема (о структуре общего решения ЛНДУ второго порядка):

Общее решение ЛНДУ второго порядка представляет собой сумму общего решения соответствующего ЛОДУ и какого-либо частного решения 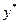, заданного ЛНДУ, т.е. .

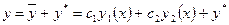Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами (ЛНДУ)

Общий вид , где 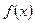- непрерывная функция при всех рассматриваемых .

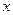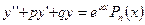- ЛНДУ второго порядка с первой специальной правой частью ( - любое действительное число, включая ноль, - многочлен - ой степени с действительными коэффициентами)

Его решение имеет вид: , где

- - общее решение соответствующего ЛОДУ ,

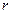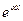- , где - кратность, с которой входит в число корней характеристического уравнения , - из 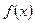, - многочлен - ой степени, взятый с буквенными коэффициентами.

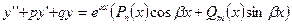- ЛНДУ второго порядка со второй специальной правой частью ( - любое действительное число, включая ноль, , 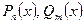- многочлен - ой и 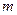- ой степени с действительными коэффициентами)

Его решение имеет вид: , где

- - общее решение соответствующего ЛОДУ ,

- , где 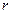- кратность, с которой пара чисел

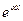рассматриваемая как единое целое, входит в число корней характеристического уравнения, - из 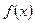, 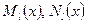- разные многочлены одной степени с буквенными коэффициентами ().

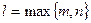ЛНДУ высших порядков решают аналогично.

Теорема:

Если 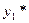- частное решение д.у. , - частное решение д.у. , то их сумма - частное решение д.у. .

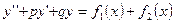6) Метод Лагранжа (для интегрирования ЛНДУ второго и высших порядков)

Этот метод целесообразно применять при интегрировании ЛНДУ с постоянными коэффициентами, но без специальной правой части и уравнений с переменными коэффициентами.

Пусть имеем 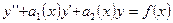- ЛНДУ второго порядка. Найдем его решение в виде методом вариации, где - решение соответствующего ЛОДУ, ;

- составляем СЛАУ относительно :

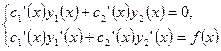
- находим по формулам Крамера решение системы: ;

- интегрируем последнее равенство и полагаем постоянные

интегрирования равными нулю, тем самым находим ;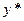

- записываем решение в виде .

Дата добавления: 2015-06-28