
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Для аналитических 1 страница
|
|
|
|
Для неаналитических
1. 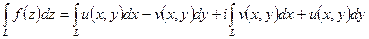
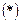 ;
;
2. В частности, если 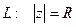 - окружность или любая его часть, то подставив
- окружность или любая его часть, то подставив  в показательной форме
в показательной форме 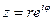 , имеем, что на окружности
, имеем, что на окружности 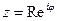 ,
, 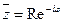 (
(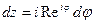 )
)
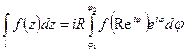
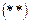 , где отрезок
, где отрезок 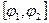 отвечает заданной части окружности.
отвечает заданной части окружности.
Замечание: формулы 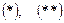 имеют место только для однозначных или отдельных ветвей многозначных функций.
имеют место только для однозначных или отдельных ветвей многозначных функций.
3. Теорема Коши (для односвязной области):
Если функция 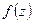 аналитическая в каждой точке области
аналитическая в каждой точке области 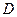 и на ее границе
и на ее границе 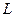 , то
, то 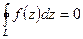 .
.
Теорема Коши (для многосвязной области):
Если функция 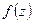 аналитическая в многосвязной области
аналитическая в многосвязной области 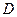 , границей которой служат кривые
, границей которой служат кривые 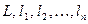 ,
,
то 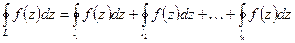 (все границы области обходятся в одном направлении)
(все границы области обходятся в одном направлении)
4. 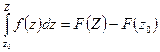 ;
;
5. Контурный интеграл от аналитической функции не зависит от формы кривой интегрирования, но зависит от начальной 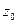 и конечной
и конечной 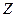 точек пути, т.е.
точек пути, т.е. 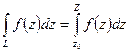 .
.
6. Используя интегральную формулу Коши, имеем:
· 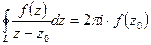 , где
, где 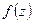 - аналитическая в односвязной области
- аналитическая в односвязной области 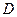 и на ее границе
и на ее границе 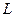
· 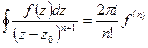 , где
, где 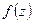 - аналитическая
- аналитическая
7. 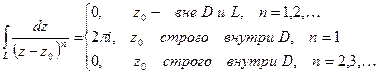
8. Теорема:
Если функция 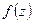 аналитическая в каждой точке области
аналитическая в каждой точке области 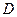 , ограниченной контуром
, ограниченной контуром 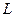 , за исключением конечного числа изолированных особых точек
, за исключением конечного числа изолированных особых точек 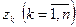 , лежащих строго внутри области
, лежащих строго внутри области 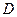 , то справедливо равенство:
, то справедливо равенство: 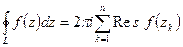 .
.
Смотри о 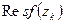 в п.4.7.
в п.4.7.
4.5. Ряды Тейлора и Лорана:
Определение: степенной ряд 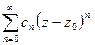 , коэффициенты которого рассчитываются по формулам
, коэффициенты которого рассчитываются по формулам 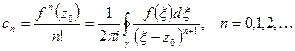 называется рядом Тейлора функции
называется рядом Тейлора функции 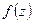 , где
, где 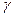 - произвольный замкнутый контур, содержащий строго внутри точку
- произвольный замкнутый контур, содержащий строго внутри точку 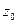 .
.
Определение: функциональный ряд вида 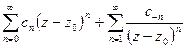 , где
, где
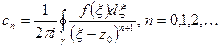 и
и 
называется рядом Лорана функции 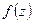 или компактная форма
или компактная форма
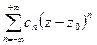 , где
, где 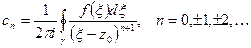
Ряд Лорана состоит из двух частей:
· 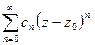 - правильная
- правильная
· 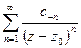 - главная часть.
- главная часть.
4.6. Типы особых точек:
Определение: точка 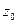 называется
называется 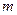 - кратным нулем функции
- кратным нулем функции 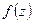 , если в разложении Тейлора этой функции в окрестности т.
, если в разложении Тейлора этой функции в окрестности т. 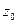
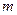 первых коэффициентов равны нулю:
первых коэффициентов равны нулю: 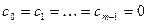 , но
, но 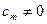 .
.
Определение: особая точка 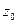 называется изолированной, если существует достаточно малая окрестность этой точки, не содержащая других особых точек данной функции.
называется изолированной, если существует достаточно малая окрестность этой точки, не содержащая других особых точек данной функции.
Определение: точка 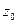 называется особой точкой функции
называется особой точкой функции 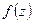 , если в этой точке функция не аналитическая.
, если в этой точке функция не аналитическая.
Определение: точка 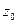 называется устранимой особой точкой
называется устранимой особой точкой 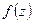 , если разложение Лорана этой функции в окрестности этой точки не содержит отрицательных степеней
, если разложение Лорана этой функции в окрестности этой точки не содержит отрицательных степеней 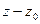 , т.е.
, т.е.
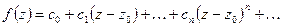
Определение: точка 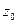 называется полюсом
называется полюсом 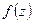 , если разложение Лорана этой функции имеет конечное число отрицательных степеней, т.е.
, если разложение Лорана этой функции имеет конечное число отрицательных степеней, т.е.
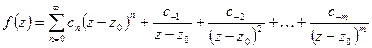 .
.
Если  , то
, то 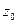 -
- 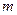 кратный полюс, если
кратный полюс, если 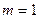 , то простой.
, то простой.
Определение: точка 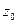 называется существенно особой точкой
называется существенно особой точкой 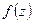 , если разложение Лорана этой функции содержит бесчисленное множество отрицательных степеней
, если разложение Лорана этой функции содержит бесчисленное множество отрицательных степеней 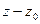 , т.е.
, т.е.
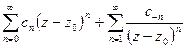 .
.
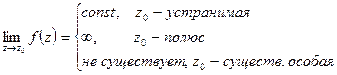
Теорема:
- 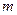 - кратный нуль функции
- кратный нуль функции 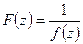 является
является 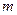 - кратным полюсом функции
- кратным полюсом функции 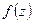 ;
;
- 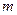 - кратный полюс функции
- кратный полюс функции 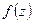 является
является 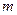 - кратным нулем функции
- кратным нулем функции 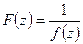 .
.
Алгоритм определения типа особой точки:
1. Применить теорему о связи между нулями и полюсами функций;
или
2. Вычислить 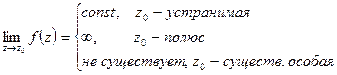 ;
;
или
3. Воспользоваться определением.
4.7. Вычеты:
Определение: число 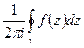 называется вычетом функции
называется вычетом функции 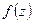 относительно изолированной точки
относительно изолированной точки 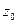 .
.
Обозначение: 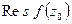 =
= 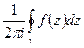 .
.
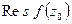 =
= 
РАЗДЕЛ V. ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
5.1. Основные понятия:
Пусть 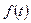 - действительная функция действительной переменной
- действительная функция действительной переменной 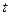 (на практике часто рассматривается как время).
(на практике часто рассматривается как время).
Определение: функция 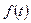 называется оригиналом, если она удовлетворяет трем условиям:
называется оригиналом, если она удовлетворяет трем условиям:
· 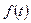 при
при 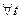 непрерывна или имеет конечное число точек разрыва первого рода;
непрерывна или имеет конечное число точек разрыва первого рода;
·  при
при 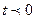 ;
;
· существуют такие действительные числа 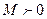 и
и 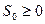 , что при
, что при 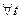
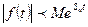 , где
, где 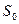 - называется показателем роста оригинала.
- называется показателем роста оригинала.
Определение: изображением оригинала 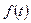 называется функция
называется функция 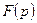 комплексной переменной
комплексной переменной 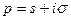 , определяемая равенством
, определяемая равенством 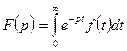 .
.
Символическая запись перехода от оригинала 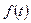 к изображению
к изображению 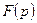 :
: 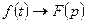 .
.
5.2. Свойства преобразований Лапласа:
1) Если 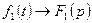 и
и 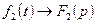 , то
, то 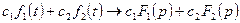 - свойство линейности;
- свойство линейности;
2) Если 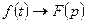 и действительное число
и действительное число 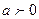 , то
, то 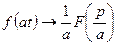 - свойство подобия;
- свойство подобия;
3) Если 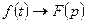 и действительное число
и действительное число 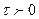 , то
, то 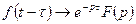 - свойство запаздывания или сдвига;
- свойство запаздывания или сдвига;
4) Если 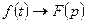 , то
, то 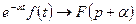 - свойство смещения или затухания;
- свойство смещения или затухания;
5) Если 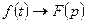 и
и 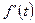 является оригиналом, то
является оригиналом, то 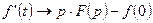 - свойство дифференцирования оригинала;
- свойство дифференцирования оригинала;
Следствие:
Если 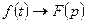 и
и 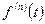 является оригиналом, то
является оригиналом, то
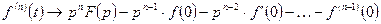 , где
, где 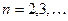
6) Если 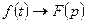 , то
, то 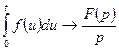 - свойство интегрирования оригинала;
- свойство интегрирования оригинала;
7) Если 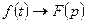 , то
, то 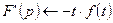 - свойство дифференцирования изображения;
- свойство дифференцирования изображения;
8) Если 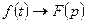 , то
, то 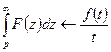 - свойство интегрирования изображения.
- свойство интегрирования изображения.
5.3. Свертка функций:
Определение: сверткой двух функций 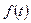 и
и 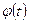 называется функция
называется функция 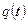 , определяемая равенством
, определяемая равенством 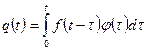 .
.
Обозначение: 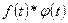 .
.
Теорема умножения изображений:
Если 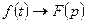 ,
, 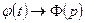 , то
, то 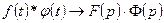 , т.е. если изображения перемножаются, то их оригиналы свертываются.
, т.е. если изображения перемножаются, то их оригиналы свертываются.
Формула обращения:
Если функция 
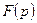 является изображением некоторого оригинала
является изображением некоторого оригинала 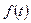 , то в каждой точке непрерывности оригинала справедлива формула
, то в каждой точке непрерывности оригинала справедлива формула  .
.
5.4. Теоремы разложения:
Теорема 1:
Если изображение 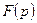 вне конечного круга
вне конечного круга 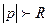 представлено рядом Лорана вида
представлено рядом Лорана вида  , то соответствующий оригинал является суммой степенного ряда
, то соответствующий оригинал является суммой степенного ряда 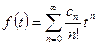 , где
, где 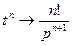 , который сходится при всех
, который сходится при всех 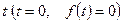 .
.
Теорема 2:
Если изображение представлено правильной рациональной дробью 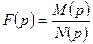 со знаменателем, имеющем только простые корни, то соответствующий оригинал находят по формуле
со знаменателем, имеющем только простые корни, то соответствующий оригинал находят по формуле 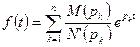 .
.
Теорема 3:
Если изображение представлено правильной рациональной дробью 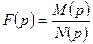 со знаменателем, имеющем кратные корни
со знаменателем, имеющем кратные корни 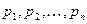 , то соответствующий оригинал находят по формуле
, то соответствующий оригинал находят по формуле 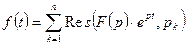 .
.
5.5. Таблица оригиналов и изображений:
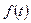 - оригинал - оригинал
| 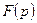 - изображение - изображение
| |
| 1. | 1 
| 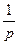
|
| 2. | 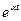
| 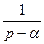
|
| 3. | 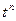
| 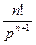
|
| 4. | 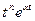
| 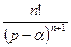
|
| 5. | 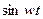
| 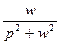
|
| 6. | 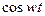
| 
|
| 7. | 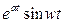
| 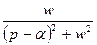
|
| 8. | 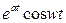
| 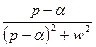
|
| 9. | 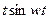
| 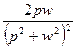
|
| 10. | 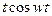
| 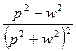
|
| 11. | 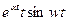
| 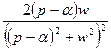
|
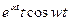
| 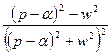
| |
| 13. | 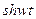
| 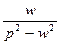
|
| 14. | 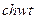
| 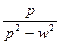
|
| 15. | 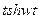
| 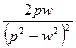
|
| 16. | 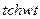
| 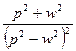
|
| 17. | 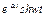
| 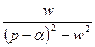
|
| 18. | 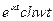
| 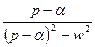
|
| 19. | 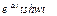
| 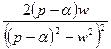
|
| 20. | 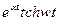
| 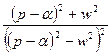
|
| 21. | 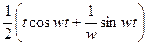
| 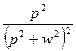
|
| 22. | 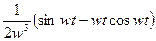
| 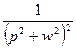
|
РАЗДЕЛ VI. ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
6.1. Элементы комбинаторики:
Определение: соединения, содержащие 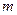 элементов из данных
элементов из данных  и отличающиеся друг от друга либо сами элементами, либо порядком их расположения в соединениях называются размещениями.
и отличающиеся друг от друга либо сами элементами, либо порядком их расположения в соединениях называются размещениями.
Формула вычисления: 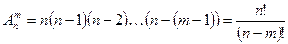
Определение: соединения, содержащие все данные  элементов и отличающиеся друг от друга только порядком расположения элементов, называются перестановками из
элементов и отличающиеся друг от друга только порядком расположения элементов, называются перестановками из  элементов.
элементов.
Формула вычисления: 
Определение: соединения, содержащие 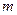 элементов из данных
элементов из данных  и отличающиеся друг от друга хотя бы одним элементом называются сочетаниями из
и отличающиеся друг от друга хотя бы одним элементом называются сочетаниями из  элементов по
элементов по 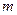 .
.
Формула вычисления: 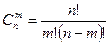 .
.
В частности, если 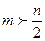 , то
, то 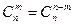 .
.
6.2. Основные понятия теории вероятностей:
Изначальные понятия: событие и вероятность.
Под событием понимают всякий факт, относительно которого уместно говорить: произойдет оно или нет.
События делят на: случайные, достоверные и невозможные.
Определение: случайным событием называют всякое явление, которое в результате осуществления комплекса условий (ОКУ) может произойти или не произойти.
Обозначение: 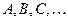
Определение: событие называется достоверным, если оно заведомо происходит при ОКУ.
Обозначение: 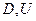 .
.
Определение: событие называется невозможным, если оно заведомо не происходит при ОКУ.
Обозначение: 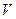
Определение: несколько событий называются равновозможными, если ни одно из них не является объективно более возможным, чем любое другое.
Определение: несколько событий называются несовместными, если появление одного из них исключает появление любого другого и совместными, если не исключает.
Определение: несколько событий образуют полную группу, если в результате ОКУ обязательно происходит хотя бы одно из данных событий.
Определение (классическое определение вероятностей): если в результате ОКУ всевозможные исходы составляют полную группу  и равновозможных и несовместных случаев, из которых
и равновозможных и несовместных случаев, из которых 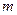 благоприятствуют появлению события
благоприятствуют появлению события  , то вероятность этого события равна отношению числа благоприятствующих событий к их общему числу.
, то вероятность этого события равна отношению числа благоприятствующих событий к их общему числу.
Т.о.  .
.
Определение: два события 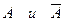 называются противоположными, если в результате ОКУ обязательно происходит одно и только одно из них.
называются противоположными, если в результате ОКУ обязательно происходит одно и только одно из них.
Теорема: 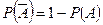 .
.
6.3. Теоремы сложения и умножения:
Определение: п роизведением двух событий называется событие, состоящее в их одновременном появлении.
Обозначение: 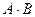
 .
.
Определение: два события 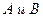 называются независимыми, если вероятность любого из них не зависит от того, произошло или не произошло другое событие и зависимыми, если зависит.
называются независимыми, если вероятность любого из них не зависит от того, произошло или не произошло другое событие и зависимыми, если зависит.
Определение: вероятность события 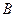 , вычисленная при условии, что событие
, вычисленная при условии, что событие  произошло, называется условной вероятностью события
произошло, называется условной вероятностью события 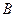 .
.
|
|
|
|
|
Дата добавления: 2015-06-28; Просмотров: 286; Нарушение авторских прав?; Мы поможем в написании вашей работы!