
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Интегральный признак Коши
|
|
|
|
Радикальный признак Коши.
Целесообразно применять, когда общий член ряда целиком является  - ой, или
- ой, или  - ой, или
- ой, или 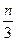 степенью какого-либо выражения.
степенью какого-либо выражения.
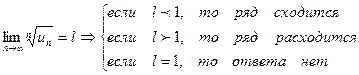 ;
;
Целесообразно применять, когда общий член ряда порождает функцию, первообразная которой находится без особого труда.
Если 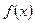 - непрерывная, положительная, убывающая в
- непрерывная, положительная, убывающая в 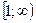 , значения которой при натуральных значениях аргумента
, значения которой при натуральных значениях аргумента 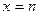 совпадают с соответствующими значениями ряда
совпадают с соответствующими значениями ряда 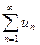 , то этот ряд и несобственный интеграл
, то этот ряд и несобственный интеграл 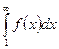 одновременно сходятся или расходятся.
одновременно сходятся или расходятся.
Исследование знакопостоянных рядов:
- проверить необходимое условие;
- применить признак Даламбера, радикальный признак Коши, интегральный признак Коши или признаки сравнения.
3.3. Знакопеременные ряды:
Определение: ряд, содержащий бесчисленное множество положительных и бесчисленное множество отрицательных членов называется знакопеременным.
Теорема (общий достаточный признак):
Если сходится ряд, составленный из абсолютных величин членов знакопеременного ряда, то сходится и знакопеременный ряд.
Определение: знакопеременный ряд, положительные и отрицательные члены которого следуют друг за другом строго поочередно, называется знакочередующимся.
Его вид: 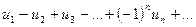 или
или 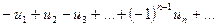 , где
, где 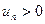 при
при 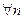 .
.
Теорема (признак Лейбница):
Если абсолютные величины членов знакочередующегося ряда убывая стремятся к нулю, то такой ряд сходится и абсолютная величина его суммы не превосходит абсолютной величины первого члена ряда.
Ряд, отвечающий условиям признака Лейбница, называется лейбницевским. Любой лейбницевским ряд сходится.
Исследование сходимости знакопеременных рядов:
- проверить необходимое условие;
- проверить для ряда условия Лейбница;
- составить ряд из абсолютных величин (если он сходится, то данный ряд сходится абсолютно; если он расходится, то данный ряд сходится условно)
3.4. Степенные ряды:
Определение: ряд, все члены которого являются функциями одного и того же аргумента называется функциональным.
Его общий вид: 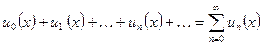 .
.
Определение: функциональный ряд вида
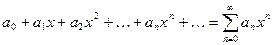 , где коэффициенты ряда
, где коэффициенты ряда 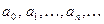 - любые действительные числа, называется степенным, расположенным по степеням
- любые действительные числа, называется степенным, расположенным по степеням 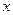 .
.
Исследование сходимости степенных рядов:
- находим радиус сходимости 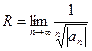 или
или  , записываем интервал сходимости;
, записываем интервал сходимости;
- проверяем поведение ряда на концах интервала;
- находим область сходимости.
3.5. Ряд Тейлора:

Ряд, стоящий в правой части равенства называется рядом Тейлора по функции 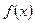 .
.
При  ряд Тейлора принимает вид:
ряд Тейлора принимает вид:

 и называется рядом Маклорена.
и называется рядом Маклорена.
3.6. Разложение элементарных функций в ряд по степеням 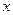 :
:
1. 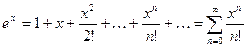 ;
; 
2.  ;
; 
3. 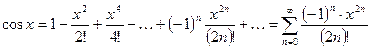 ;
; 
4.  ;
; 
5.  ;
; 
6. 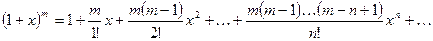
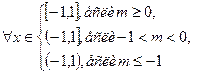
7. 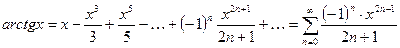 ;
; 
8. 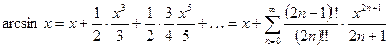 ;
; 
9.  ;
; 
10. 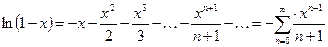 ;
; 
11. 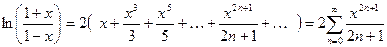 ;
; 
3.7. Ряды Фурье. Теорема Дирихле.
Определение: функция 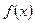 , называется удовлетворяющей условиям Дирихле на
, называется удовлетворяющей условиям Дирихле на 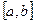 , если она на этом отрезке
, если она на этом отрезке
· непрерывна или имеет конечное число точек разрыва первого рода;
· имеет конечное число строгих экстремумов.
Теорема Дирихле (достаточное условие разложимости функции в ряд Фурье):
Если функция 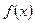 отвечает на отрезке
отвечает на отрезке 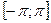 условиям Дирихле, то ее ряд Фурье сходится в каждой точке этого отрезка, причем во внутренних точках непрерывности функции
условиям Дирихле, то ее ряд Фурье сходится в каждой точке этого отрезка, причем во внутренних точках непрерывности функции 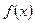 ряд сходится к самой функции
ряд сходится к самой функции  . В каждой внутренней точке разрыва
. В каждой внутренней точке разрыва 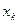 функции
функции 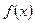 ряд сходится к среднему арифметическому предельных значений этой функции в точке
ряд сходится к среднему арифметическому предельных значений этой функции в точке 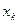 слева и справа, т.е.
слева и справа, т.е. 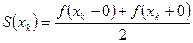 . В обеих граничных точках
. В обеих граничных точках 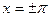 ряд сходится к среднему арифметическому предельных значений функции в этих точках, когда
ряд сходится к среднему арифметическому предельных значений функции в этих точках, когда 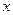 стремится к ним изнутри отрезка, т.е.
стремится к ним изнутри отрезка, т.е. 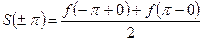 .
.
Алгоритм разложения периодических функции в ряд Фурье на 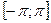 :
:
- строим график на 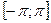 и с его помощью проверяем выполнение условий Дирихле;
и с его помощью проверяем выполнение условий Дирихле;
- устанавливаем ожидаемую форму ряда Фурье;
- вычисляем коэффициенты по формулам Эйлера-Фурье и составляем формальный ряд;
- строим на заданном отрезке график суммы 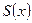 ряда;
ряда;
- периодически продолжаем графики функции и суммы на всю числовую ось;
- определяем точки сходимости ряда к самой функции 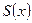 ;
;
Аналогично, раскладываются в ряд Фурье периодические функции на  ;
; 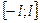 ;
; 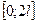 .
.
Если 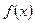 - общего положения на
- общего положения на 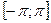 , то ее можно разложить в ряд Фурье вида:
, то ее можно разложить в ряд Фурье вида:
 , где
, где 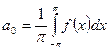 ;
;
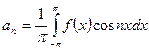 , где
, где 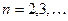
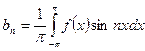 , где
, где 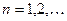
Если 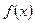 - общего положения на
- общего положения на 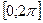 , то ее можно разложить в ряд Фурье вида:
, то ее можно разложить в ряд Фурье вида:
 , где
, где  ;
;
 , где
, где 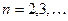
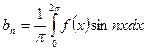 , где
, где 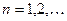
Если 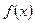 - общего положения на
- общего положения на  , то ее можно разложить в ряд Фурье вида:
, то ее можно разложить в ряд Фурье вида:
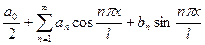 , где
, где 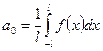 ;
;
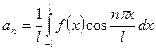 , где
, где 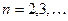
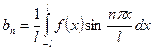 , где
, где 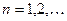
Алгоритм разложения в ряд Фурье непериодических функций, заданных на 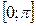 ;
; 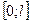 по косинусам (по синусам):
по косинусам (по синусам):
- продолжаем функцию 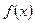 четным (нечетным) образом на
четным (нечетным) образом на  (
( ) и получаем новую функцию
) и получаем новую функцию 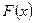 ;
;
- строим график 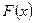 и проверяем условия Дирихле;
и проверяем условия Дирихле;
- устанавливаем ожидаемую форму ряда Фурье;
- вычисляем коэффициенты по формулам Эйлера-Фурье и составляем формальный ряд 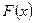 ;
;
- строим на заданном отрезке график суммы 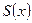 ряда;
ряда;
- определяем точки сходимости ряда к самой функции 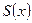 ;
;
Если 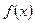 - четная на
- четная на 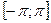 , то ее можно разложить в ряд Фурье вида:
, то ее можно разложить в ряд Фурье вида:
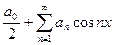 , где
, где  ;
;
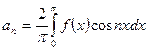 , где
, где 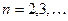
Если 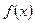 - нечетная на
- нечетная на 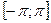 , то ее можно разложить в ряд Фурье вида:
, то ее можно разложить в ряд Фурье вида:
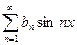 , где
, где 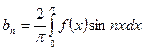 , где
, где 
При вычислении интегралов, учитываем, что 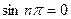 и
и 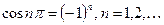
РАЗДЕЛ IV. ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОГО
|
|
|
|
|
Дата добавления: 2015-06-28; Просмотров: 529; Нарушение авторских прав?; Мы поможем в написании вашей работы!