
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Для аналитических 3 страница
|
|
|
|
6. Находят число степеней свободы 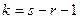 , где
, где
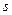 - количество частичных областей выборки;
- количество частичных областей выборки;
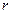 - число параметров исследуемого распределения.
- число параметров исследуемого распределения.
7. По таблице определяют критическую точку 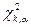 .
.
8. Сравнивают 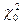 и
и 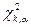 . Если
. Если 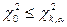 , то гипотеза
, то гипотеза 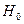 принимается, если
принимается, если 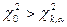 , то гипотеза
, то гипотеза 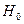 отвергается и принимается гипотеза
отвергается и принимается гипотеза 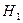 .
.
7.5. Лабораторная работа по теме «Статистическая проверка гипотез. критерий пирсона»
Студента __________класса
Ф.И. _________________________________________________
Вариант №___________________
1. Построить полигон и гистограмму.
2. Используя критерий Пирсона при уровне значимости 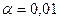 , проверить гипотезу о нормальном распределении генеральной совокупности.
, проверить гипотезу о нормальном распределении генеральной совокупности.
3. Если генеральная совокупность распределена нормально, то найти доверительные интервалы для параметров 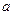 и
и  с надежностью
с надежностью 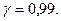
| ||||||||
| ||||||||
| ||||||||
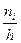
|

ХОД ЛАБОРАТОРНОЙ РАБОТЫ:
1. Используя таблицу, строим полигон - ломаную, соединяющую точки 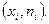 , если нет
, если нет 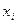 , то находим их как середину интервала
, то находим их как середину интервала 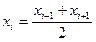 .
.
2. Используя таблицу, строим гистограмму – ступенчатую фигуру (совокупность прямоугольников с основаниями 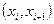 и высотой
и высотой 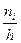 , где
, где  .
.
3. Выдвигается основная гипотеза 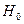 - относительно закона распределения данной генеральной совокупности:
- относительно закона распределения данной генеральной совокупности:
_____________________________________________________
и ей альтернативная 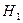
_____________________________________________________
4. По данной выборке составляем допустимый статистический ряд: если число значений вариант в некоторых частичных областях меньше пяти 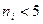 , то такие области объединяем с соседними, если этого нет, таблица остается без изменения и этот пункт пропускаем.
, то такие области объединяем с соседними, если этого нет, таблица остается без изменения и этот пункт пропускаем.
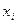
| ||||||||
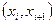
| ||||||||
|
5. По данным выборки вычисляем параметры предполагаемого распределения генеральной совокупности 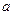 и
и  , статистическими оценками которых являются
, статистическими оценками которых являются 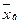 и
и 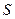 :
:
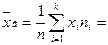 _______________________________________________________________
_______________________________________________________________
________________________________________________________________
_____________
 ________________________________________________
________________________________________________
________________________________________________________________
6. Находим вероятности 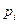 попадания с.в.
попадания с.в. 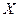 в каждую частичную область по формуле
в каждую частичную область по формуле
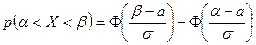 :
:
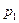 =_____________________________________________________________
=_____________________________________________________________
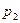 =_____________________________________________________________
=_____________________________________________________________
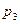 =_____________________________________________________________
=_____________________________________________________________
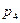 =_____________________________________________________________
=_____________________________________________________________
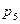 =_____________________________________________________________
=_____________________________________________________________
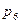 =_____________________________________________________________
=_____________________________________________________________
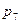 =_____________________________________________________________
=_____________________________________________________________
 =_____________________________________________________________
=_____________________________________________________________
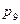 =_____________________________________________________________
=_____________________________________________________________
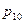 =_____________________________________________________________
=_____________________________________________________________
7. Составляем гипотетический ряд распределения выборки:
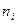
| |||||||||
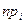
|
8. Находим по формуле  =
=
________________________________________________________________
________________________________________________________________
9. Находим число степеней свободы 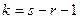 =___________________, где
=___________________, где
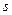 - количество частичных областей выборки.
- количество частичных областей выборки.
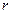 - число параметров исследуемого распределения.
- число параметров исследуемого распределения.
10. По таблице определяем критическую точку 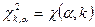 =______________________
=______________________
11. Сравниваем 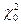 и
и 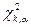 :
:
_____________________________________________________
________________________________________________________________
12. Найдем доверительный интервал для 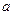 и
и  с надежностью
с надежностью 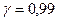 :
:
1) 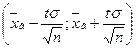 - доверительный интервал для
- доверительный интервал для 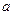
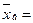 ________;
________; 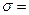 ________;
________; 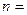 ________.
________.
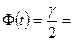 ___________
___________ 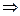
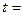 _________.
_________.
________________________________________________________________
Итак, доверительный интервал для 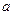 :
:
____________________________________
2)  _________
_________
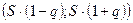 - доверительный интервал для
- доверительный интервал для  :
:
________________________________________________________________
|
|
|
|
|
Дата добавления: 2015-06-28; Просмотров: 322; Нарушение авторских прав?; Мы поможем в написании вашей работы!