Лабораторная работа: «Корреляционный анализ»

Лабораторная работа: «Метод наименьших квадратов».

Студента _________класса,

Ф.И.__________________________________________________

Вариант № ___________

Цель лабораторной работы: по данным таблицы получить аналитическую зависимость функции .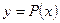

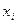
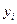
Ход лабораторной работы:

1. Определяем степень многочлена 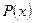, т.е. строим точки , где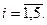

2. Если 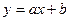, то найдем 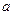и 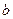, решая систему вида:

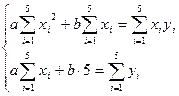
Чтобы ее решить, составим вспомогательную таблицу:

№
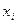
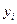
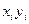
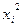
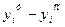
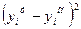
1.
2.
3.
4.
5.

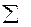
Решим систему по формулам Крамера:

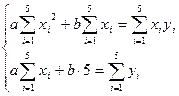
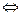
Т.о. 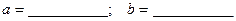и .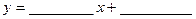

Строим график полученной функции (ручкой другого цвета), для этого возьмем две ее точки, например: 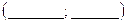и .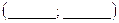

3. Делаем вывод, для этого вычисляем:

и находим

Студента ___________класса

Ф.И.__________________________________________________________

Вариант ________________

1. Составить уравнение линейной регрессии 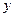на 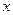, Изобразить её геометрически.

2. Определить тесноту связи между с.в. 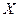и 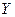с помощью коэффициента корреляции

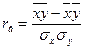и геометрически.

сер.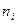

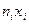
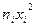
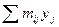
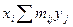
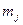
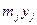
1. Составляем уравнение связи между случайными величинами- уравнение линейной регрессии 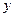на : :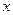

.

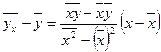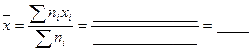
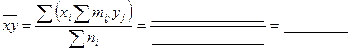Т.о. уравнение линейной регрессии примет вид:

,

,

.

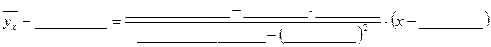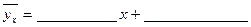Изобразим графически линейную регрессию, для этого возьмем две точк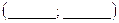и и .

2. Определить тесноту связи между с.в. 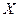и 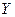с помощью коэффициента корреляции

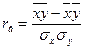и геометрически:

Т.о.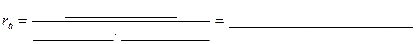

СОДЕРЖАНИЕ

Введение 3

НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ЭЛЕМЕНТАРНОЙ

МАТЕМАТИКИ 4

1 КУРС

РАЗДЕЛ I. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ 11

1.1. Основные действия над матрицами 11

1.2. Элементарные преобразования над матрицами 11

1.3. Вычисление определителей 12

1.4. Свойства определителей 13

1.5. Обратная матрица 13

1.6. Свойства обратной матрицы 13

1.7. Формулы Крамера 14

1.8. Теорема о числе решений совместных систем 14

1.9. Метод Гаусса 15

1.10. Однородные системы линейных уравнений 16

РАЗДЕЛ II. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ 18

2.1. Основные понятия 18

2.2. Линейные операции над векторами 19

2.3. Скалярное произведение векторов 20

2.4. Векторное произведение векторов 21

2.5. Смешанное произведение векторов 22

РАЗДЕЛ III. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ 24

3.1. Задачи на точку 24

3.2. Прямоугольная и полярная системы координат 24

3.3. Связь прямоугольной и полярной систем координат 25

3.4. Виды уравнений прямой на плоскости 25

3.5. Задачи на прямую на плоскости 27

3.6. Уравнения окружности 27

3.7. Эллипс 28

3.8. Парабола 29

3.9. Гипербола 30

3.10. Плоскость в пространстве 31

3.11. Задачи на плоскость в пространстве 32

3.12. Прямая в пространстве 32

3.13. Задачи на прямую в пространстве 33

3.14. Задачи на прямую и плоскость в пространстве 33

3.15. Цилиндрические поверхности 34

РАЗДЕЛ IV. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА 36

РАЗДЕЛ V. ГРАФИКИ ОСНОВНЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ 37

РАЗДЕЛ VI. УРАВНЕНИЯ И ГРАФИКИ КРИВЫХ В П.С.К. 41

РАЗДЕЛ VII. КРИВЫЕ, ЗАДАННЫЕ ПАРАМЕТРИЧЕСКИ 42

РАЗДЕЛ VIII. НАХОЖДЕНИЕ ПРЕДЕЛОВ 43

8.1. Определение пределов 43

8.2. БМФ и ББФ, непрерывность функции 44

8.3. Алгоритм нахождения пределов от алгебраических функций 45

8.4. Замечательные пределы 46

8.5. Нахождение пределов с использованием БМФ 46

РАЗДЕЛ IX. ПРОИЗВОДНАЯ ФУНКЦИИ 48

9.1. Определение производной. Геометрический и механический

смысл 48

9.2. Дифференциал функции 48

9.3. Таблица производных 49

9.4. Логарифмическое дифференцирование 49

9.5. Дифференцирование функций, заданных неявно 50

9.6. Дифференцирование функций, заданных параметрически 50

9.7. Производные высших порядков 50

9.8. Раскрытие неопределенностей по правилу Лопиталя 51

9.9. Формула Тейлора 52

9.10. Общая схема исследования функции и построение ее графика 53

РАЗДЕЛ X. КОМПЛЕКСНЫЕ ЧИСЛА 54

10.1. Основные понятия 54

10.2. Действия над комплексными числами 55

РАЗДЕЛ XI. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 56

11.1. Определение и свойства неопределенного интеграла 56

11.2. Таблица интегралов и дифференциалов 56

11.3. Общие методы интегрирования 58

РАЗДЕЛ XII. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 64

12.1. Определение и свойства определенного интеграла 64

12.2. Методы вычисления 65

12.3. Несобственные интегралы 65

12.4. Применения определенного интеграла 66

РАЗДЕЛ XIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ

НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 69

13.1. Основные понятия 69

13.2. Частные производные 70

13.3. Дифференцирование сложных функций 71

13.4. Дифференцирование неявных функций 71

13.5. Касательная плоскость и нормаль к поверхности 71

13.6. Экстремумы функции двух переменных 72

РАЗДЕЛ XIV. КРАТНЫЕ ИНТЕГРАЛЫ 73

14.1. Определение и свойства двойного интеграла 73

14.2. Вычисление двойного интеграла 74

14.3. Применения двойного интеграла 75

14.4. Определение и свойства тройного интеграла 75

14.5. Применения тройного интеграла 77

РАЗДЕЛ XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ 79

15.1. Криволинейный интеграл по длине дуги (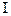 рода) 79

15.2. Вычисление криволинейного интеграла по длине дуги 79

15.3. Применения криволинейного интеграла по длине дуги 80

15.4. Криволинейный интеграл по координатам (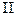 рода) 80

15.5. Вычисление криволинейного интеграла по координатам 81

15.6. Применения криволинейного интеграла по координатам 82

РАЗДЕЛ XVI. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ 83

16.1. Поверхностный интеграл по площади поверхности (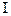 рода) 83

16.2. Вычисление поверхностного интеграла по площади

поверхности 84

16.3. Применения поверхностного интеграла по площади

поверхности 84

16.4. Поверхностный интеграл по координатам (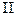 рода) 85

16.5. Вычисление поверхностного интеграла по координатам 86

2 КУРС

РАЗДЕЛ I. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ

УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА 87

1.1. Основные понятия 87

1.2. Типы дифференциальных уравнений первого порядка 87

1.3. Д.У. высших порядков 89

1.4. Системы дифференциальных уравнений 92

РАЗДЕЛ II. ТЕОРИЯ ПОЛЯ 94

2.1. Скалярное поле и его характеристики 94

2.2. Векторное поле и его характеристики 94

РАЗДЕЛ III. РЯДЫ 97

3.1. Основные понятия 97

3.2. Знакопостоянные ряды 97

3.3. Знакопеременные ряды 99

3.4. Степенные ряды 100

3.5. Ряд Тейлора 100

3.6. Разложение элементарных функций в ряд по степеням х 100

3.7. Ряды Фурье. Теорема Дирихле 101

РАЗДЕЛ IV. ТФКП 104

4.1. Основные понятия 104

4.2. Основные элементарные функции 105

4.3. Определения и свойства контурного интеграла по кривой 106

4.4. Вычисление контурного интеграла 107

4.5. Ряды Тейлора и Лорана 108

4.6. Типы особых точек 109

4.7. Вычеты 110

РАЗДЕЛ V. ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ 111

5.1. Основные понятия 111

5.2. Свойства преобразований Лапласа 111

5.3. Свертка функций 112

5.4. Теоремы разложения 112

5.5. Таблица оригиналов и изображений 113

РАЗДЕЛ VI. ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ 115

6.1. Элементы комбинаторики 115

6.2. Основные понятия теории вероятностей 115

6.3. Теоремы сложения и умножения 116

6.4. Случайные величины 119

6.5. Числовые характеристики случайных величин 121

РАЗДЕЛ VII. СТАТИСТИКА 124

7.1. Основные понятия 124

7.2. Числовые характеристики генеральной и выборочной

совокупностей 125

7.3. Доверительный интервал для параметров нормального

распределения 125

7.4. Статистическая проверка гипотез 126

7.5. Лабораторная работа «Статистическая проверка гипотез.

Критерий Пирсона» 126

7.6. Лабораторная работа «Метод наименьших квадратов» 131

7.7. Лабораторная работа «Корреляционный анализ» 133

Дата добавления: 2015-06-28