
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные теоремы об эквивалентных бмф 2 страница
|
|
|
|
Алгоритм нахождения  :
:
1) Вводим новую переменную интегрирования 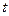 .
.
2) Представляем заданное подынтегральное выражение в переменных 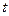 и
и 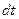 .
.
3) Берем интеграл с новой переменной.
4) В полученной первообразной заменяем переменную 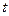 на
на 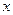 .
.
Применяется в случае:
- если 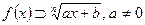 , то
, то 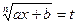 ;
; 
- если 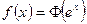 , то
, то 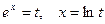 ;
;
- если 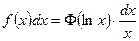 , то
, то 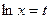 ;
;
- если  , то
, то  ;
;
- если 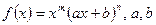 - действительные числа
- действительные числа 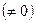 ,
,
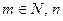 - любое
- любое 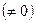 ,
, 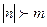 , то
, то 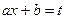 .
.
3. Интегрирование по частям:
Применяется при интегрировании специально подобранных функций.
 - формула интегрирования по частям, где
- формула интегрирования по частям, где  - непрерывно-дифференцируемы при всех рассматриваемых
- непрерывно-дифференцируемы при всех рассматриваемых 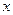 .
.
Алгоритм нахождения  :
:
1) Разбиваем заданное подынтегральное выражение 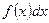 на два множителя
на два множителя 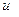 и
и 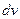 .
.
2) Находим 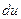 и
и 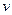 .
.
3) К заданному интегралу применяем формулу 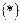 .
.
Классы функций, интегрируемых по частям:
1 класс:  =
= 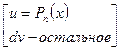
 - многочлен любой степени, кроме нуля,
- многочлен любой степени, кроме нуля,  - любое ненулевое действительное число.
- любое ненулевое действительное число.
2 класс: 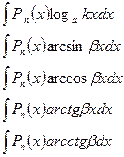 =
= 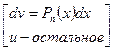
 - многочлен любой степени, включая нулевую,
- многочлен любой степени, включая нулевую,  - любое ненулевое действительное число.
- любое ненулевое действительное число.
3 класс:  =
= 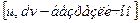
 - любое ненулевое действительное число.
- любое ненулевое действительное число.
Замечания:
1) При нахождении интегралов первого класса формулу интегрирования по частям применяют столько раз, какова степень данного многочлена  .
.
2) Нахождение интегралов третьего класса в итоге сводится к решению уравнения относительно заданного интеграла.
4. Интегрирование рациональных дробей:
Алгоритм нахождения 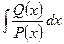 :
:
- Проверяем, является ли заданная рациональная дробь  правильной, если дробь неправильная, то представляем ее в виде суммы целой части и правильной рациональной дроби (для этого в общем случае делим числитель на знаменатель, в частности используем формулы сокращенного умножения)
правильной, если дробь неправильная, то представляем ее в виде суммы целой части и правильной рациональной дроби (для этого в общем случае делим числитель на знаменатель, в частности используем формулы сокращенного умножения)
- Раскладываем правильную рациональную дробь на сумму простейших методом неопределенных коэффициентов.
Определение: правильные рациональные дроби вида
 , где
, где 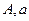 - любые действительные числа
- любые действительные числа 
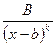 , где
, где  - любые действительные числа,
- любые действительные числа, 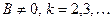
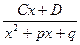 , где
, где 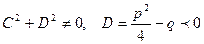
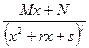 , где
, где 
называются простейшими дробями 1-4 типов.
Алгоритм представления правильной рациональной дроби в виде суммы простейших дробей:
- каждому простому действительному корню  или его множителю
или его множителю 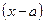 знаменателя соответствует одна дробь
знаменателя соответствует одна дробь  ;
;
- каждому  кратному действительному корню
кратному действительному корню 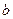 или его множителю
или его множителю 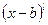 знаменателя соответствуют одна дробь
знаменателя соответствуют одна дробь 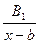 и
и 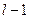 дробь:
дробь: 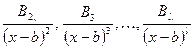
- каждой простой паре комплексно-сопряженных корней знаменателя соответствует одна дробь 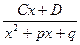 ;
;
- каждой 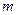 - кратной паре комплексно-сопряженных корней знаменателя соответствуют дробь
- кратной паре комплексно-сопряженных корней знаменателя соответствуют дробь 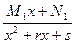 и
и  дробь:
дробь: 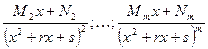
Алгоритм нахождения коэффициентов разложения правильной рациональной дроби (метод неопределенных коэффициентов):
- приводим правую часть разложения к общему знаменателю, получаем тождественное равенство двух дробей с одинаковыми знаменателями;
- отбрасываем эти знаменатели, получаем тождество из числителей;
- в последнем тождестве последовательно придаем значения действительных корней знаменателя исходной дроби, если они есть, а затем нужное число раз сравниваем коэффициенты при одинаковых степенях 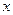 . Получаем СЛАУ относительно искомых коэффициентов;
. Получаем СЛАУ относительно искомых коэффициентов;
- решив СЛАУ, находим коэффициенты, и значит, само разложение;
- интегрируем простейшие дроби и, если есть, целую часть:
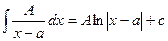
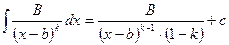
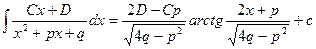
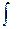
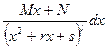 - интегрируем либо по формуле Остроградского, либо с помощью реккурентных преобразований.
- интегрируем либо по формуле Остроградского, либо с помощью реккурентных преобразований.
5. Интегрирование функций, рационально зависящих от тригонометрических:
1. 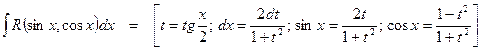
2. 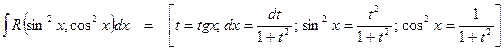
3. 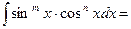
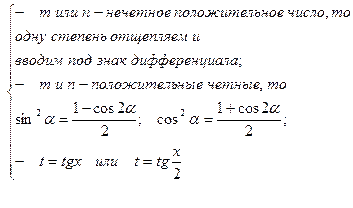
4. 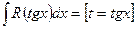 ;
; 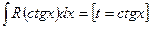
5. 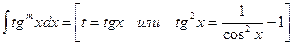 ;
;
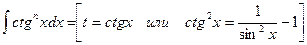 .
.
6. 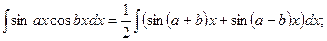

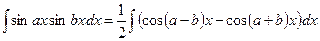 .
.
6. Интегрирование простейших алгебраических иррациональностей:
1) 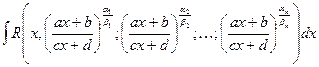 , где
, где  - любые действительные числа,
- любые действительные числа, 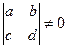 ,
, 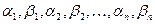 - любые натуральные числа, составляющие несократимые дроби.
- любые натуральные числа, составляющие несократимые дроби.
Здесь 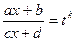 , где
, где 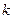 - общий знаменатель дробей
- общий знаменатель дробей 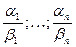 ;
;
2) 
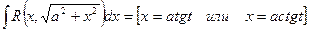
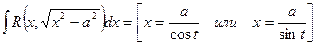 , где
, где 
3) 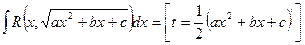 , где
, где 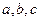 -любые
-любые
действительны числа неравные нулю.
4) 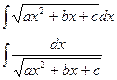 - выделяем полный квадрат под знаком корня.
- выделяем полный квадрат под знаком корня.
5) 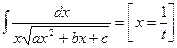 ;
;
6) 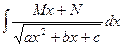 - в числителе получают дифференциал подкоренного выражения;
- в числителе получают дифференциал подкоренного выражения;
7) 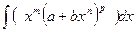 , где
, где 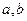 - любые неравные нулю действительные числа,
- любые неравные нулю действительные числа, 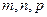 - рациональные числа
- рациональные числа 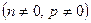 :
:
- если 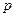 - целое, то полагают
- целое, то полагают 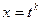 , где
, где 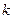 - общий знаменатель дробей
- общий знаменатель дробей 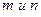 ;
;
- если  - целое, то
- целое, то 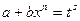 , где
, где 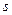 - знаменатель дроби
- знаменатель дроби 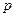 ;
;
- если 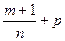 - целое, то
- целое, то 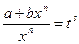 , где
, где 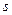 - знаменатель дроби
- знаменатель дроби 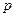 .
.
Неберущиеся интегралы:
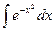 ;
; 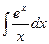 ;
; 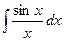 ;
; 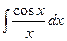 ;
;  ;
; 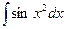 ;
; 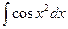 ;
;
 .
.
РАЗДЕЛ XII. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
12.1. Определение и свойства определенного интеграла:

 Определение: конечный предел интегральной суммы функции
Определение: конечный предел интегральной суммы функции  на
на 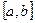 называется определенным интегралом от этой функции на
называется определенным интегралом от этой функции на 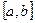 .
.
Т.о. 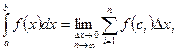 , где
, где  .
.
Теорема (формула Ньютона-Лейбница): Определенный интеграл от непрерывной функции равен разности двух значений любой первообразной подынтегральной функции, взятых при верхнем и нижнем пределах интегрирования: 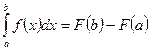 .
.
Основные свойства определенного интеграла:
1) 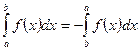 ;
;
2)  ;
;
3) 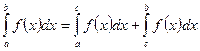 - свойство аддитивности
- свойство аддитивности
4) Если на 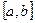 , где
, где 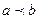
 , то и
, то и 
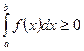 ;
;
5) Интегрирование неравенств:
Если на 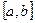 , где
, где 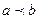
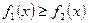 , то и
, то и 
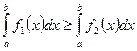 ;
;
6) Об оценке определенного интеграла:
Если 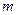 - наименьшее,
- наименьшее, 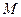 - наибольшее значения функции
- наибольшее значения функции  на
на 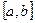 , то
, то 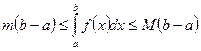
7)  ;
;
8) Теорема о среднем:  , где
, где 
9) 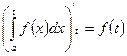 .
.
12.2. Методы вычисления определенного интеграла:
- Непосредственное интегрирование (применение формулы Ньютона-Лейбница);
- Замена переменной интегрирования: 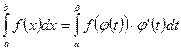 . Здесь не возвращаются к исходной переменной, но сразу вводят новые пределы интегрирования.
. Здесь не возвращаются к исходной переменной, но сразу вводят новые пределы интегрирования.
- Интегрирование по частям: если  - непрерывно-дифференцируемы на
- непрерывно-дифференцируемы на 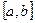 , то
, то 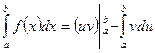 .
.
Все замечания, сделанные к аналогичному методу в неопределенном интеграле, остаются справедливыми.
- Определенный интеграл на отрезке симметричном нулю от нечетной функции равен нулю, от четной – двум интегралам, взятым по половине исходного отрезка интегрирования:

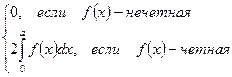 .
.
12.3. Несобственные интегралы:
Первого рода:
Пусть  - непрерывна на
- непрерывна на 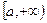 или на
или на  :
:
1.  или
или 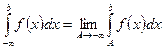 ,
,
если эти пределы существуют и конечны, то соответствующий несобственный интеграл называется сходящимся, если не существует или равен бесконечности, то расходящимся.
2. 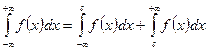 , где
, где  - любая точка оси
- любая точка оси  .
.
Полный интеграл 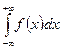 сходится, тогда и только тогда, когда сходится каждый из составляющих его интегралов.
сходится, тогда и только тогда, когда сходится каждый из составляющих его интегралов.
Второго рода:
Пусть  - непрерывна в
- непрерывна в 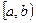 или
или 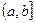 :
:
1.  или
или 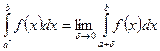 ,
,
если эти пределы существуют и конечны, то соответствующий несобственный интеграл называется сходящимся, если не существует или равен бесконечности, то расходящимся.
2. 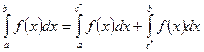 , где
, где  - внутренняя точка бесконечного разрыва.
- внутренняя точка бесконечного разрыва.
Такой несобственные интеграл, сходится тогда и только тогда, когда сходятся оба составляющих его интеграла.
12.4. Применения определенного интеграла:
1. Вычисление площадей плоских фигур:
· 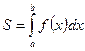 - площадь криволинейной трапеции,
- площадь криволинейной трапеции,
где 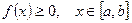 ;
;
· 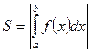 - площадь криволинейной трапеции,
- площадь криволинейной трапеции,
где 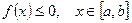 ;
;
· 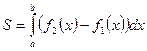 - площадь фигуры, где
- площадь фигуры, где 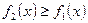 ,
, 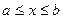 ;
;
· 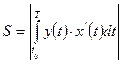 -площадь фигуры, где основная кривая задана как
-площадь фигуры, где основная кривая задана как
 , где
, где 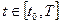 ,
, 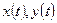 - непрерывно-дифференцируемы на
- непрерывно-дифференцируемы на  ;
;
·  - площадь фигуры, где основная кривая задана в п.с.к.
- площадь фигуры, где основная кривая задана в п.с.к.
уравнением 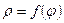 ,
, 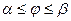 .
.
2. Вычисление длин дуг плоских кривых:
· 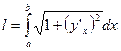 - формула вычисления длины дуги, заданной явно
- формула вычисления длины дуги, заданной явно  , где
, где  - непрерывно-дифференцируема на
- непрерывно-дифференцируема на 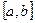
· 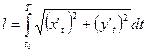 - для дуги, заданной параметрически
- для дуги, заданной параметрически  , где
, где 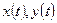 - непрерывно-дифференцируемы на
- непрерывно-дифференцируемы на  .
.
· 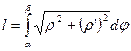 - для дуги кривой в п.с.к., где
- для дуги кривой в п.с.к., где 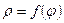 и
и 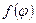 - непрерывно-дифференцируема на
- непрерывно-дифференцируема на 
3. Вычисление площадей поверхностей вращения:
· 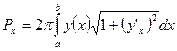 - вокруг оси
- вокруг оси 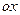 ;
;
· 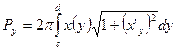 - вокруг оси
- вокруг оси 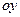 ;
;
· 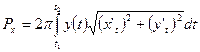 - для кривой, заданной параметрически;
- для кривой, заданной параметрически;
·  - для кривой в п.с.к.
- для кривой в п.с.к.
4. Вычисление объемов тел вращения:
·  - вокруг оси
- вокруг оси 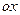 ;
;
· 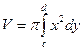 - вокруг оси
- вокруг оси 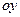 .
.
5. Физические приложения определенного интеграла:
· 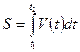 -формула нахождения пути по скорости при прямолинейном движении;
-формула нахождения пути по скорости при прямолинейном движении;
· 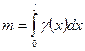 - масса неоднородного стержня длины
- масса неоднородного стержня длины  с заданной линейной плотностью
с заданной линейной плотностью 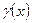 ;
;
· 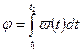 - угол поворота за отрезок времени
- угол поворота за отрезок времени 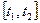 при заданной угловой скорости
при заданной угловой скорости 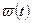 ;
;
·  - количество теплоты необходимое для нагревания тела от
- количество теплоты необходимое для нагревания тела от 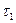 до
до 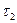 при заданной теплоемкости
при заданной теплоемкости 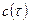 ;
;
· 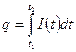 - количество электричества, протекающего через поперечное сечение проводника за отрезок времени
- количество электричества, протекающего через поперечное сечение проводника за отрезок времени 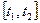 при заданной силе тока
при заданной силе тока 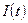 ;
;
· 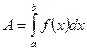 - работа переменной силы
- работа переменной силы  при прямолинейном перемещении из положения
при прямолинейном перемещении из положения 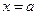 в положение
в положение  (физический смысл определенного интеграла);
(физический смысл определенного интеграла);

· 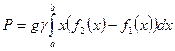 - формула вычисления давления жидкости на вертикальную пластину (
- формула вычисления давления жидкости на вертикальную пластину (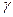 - плотность жидкости).
- плотность жидкости).
РАЗДЕЛ XIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ
|
|
|
|
|
Дата добавления: 2015-06-28; Просмотров: 419; Нарушение авторских прав?; Мы поможем в написании вашей работы!