
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
В полярной системе координат 2 страница
|
|
|
|
2.5. Смешанное произведение векторов:
Определение: смешенным произведением трех ненулевых векторов  называется произведение, в котором два первых вектора перемножаются векторно, а их результат скалярно на третий вектор.
называется произведение, в котором два первых вектора перемножаются векторно, а их результат скалярно на третий вектор.
Обозначение: 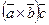 или
или  .
.
1) 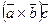 - число
- число
2)  Геометрический смысл:
Геометрический смысл:
 - объем параллелепипеда, построенного на векторах, как на ребрах
- объем параллелепипеда, построенного на векторах, как на ребрах
(с “+”, если тройка правая, с “-“, если тройка левая).
 - объем параллелепипеда.
- объем параллелепипеда.
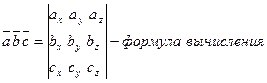 , где
, где 
 ,
,  .
.
Свойства:
1) 
2) При круговой перестановке смешанное произведение не изменяется: 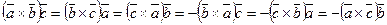
Приложения:
- 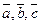 -компланарны
-компланарны 
- если 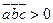 , то тройка правая;если
, то тройка правая;если 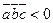 , то тройка левая;
, то тройка левая;
-  -объем параллелепипеда,
-объем параллелепипеда,
 -объем пирамиды.
-объем пирамиды.
РАЗДЕЛ III. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
3.1. Задачи на точку:
1) Если 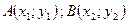 , то середина отрезка -
, то середина отрезка -  ;
;
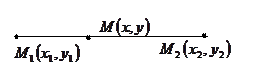 2)
2)  -деление отрезка в заданном отношении
-деление отрезка в заданном отношении 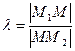 .
.
3) Если 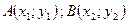 , то
, то 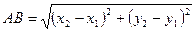 - расстояние между точками
- расстояние между точками 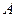 и
и  .
.
3.2. Прямоугольная и полярная системы координат:
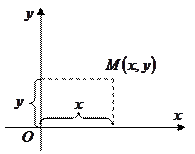
Прямоугольная система координат задается двумя взаимно перпендикулярными осями:
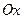 - ось абсцисс и
- ось абсцисс и 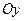 - ось ординат.
- ось ординат.
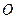 - начало координат.
- начало координат.
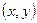 - прямоугольные координаты точки, где
- прямоугольные координаты точки, где  - абсцисса,
- абсцисса, 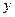 - ордината.
- ордината.
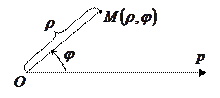 Полярная система координат задается лучом - поляной осью
Полярная система координат задается лучом - поляной осью  и полюсом - точкой
и полюсом - точкой 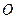 .
.
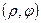 - полярные координаты,
- полярные координаты,
где 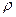 - полярный радиус,
- полярный радиус,  - полярный угол.
- полярный угол.  ,
, 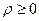 .
.
3.3. Связь прямоугольной и полярной систем координат:

Прямоугольные координаты через полярные:  .
.
Полярные координаты через прямоугольные:
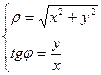 , где
, где

3.4.Виды уравнений прямой на плоскости:

1)  - нормальное уравнение прямой (
- нормальное уравнение прямой (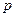 - перпендикуляр, опущенный из начала координат на прямую)
- перпендикуляр, опущенный из начала координат на прямую)
2) 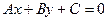 - общее уравнение прямой, где
- общее уравнение прямой, где 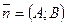 - нормальный вектор прямой.
- нормальный вектор прямой.
С помощью нормирующего множителя 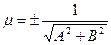 сводят общее уравнение к нормальному.
сводят общее уравнение к нормальному.
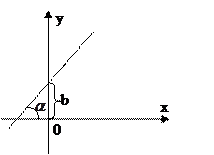
3) 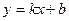 - уравнение с угловым коэффициентом (b-ордината точки пересечения прямой с oy,
- уравнение с угловым коэффициентом (b-ордината точки пересечения прямой с oy, 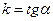 - угловой коэффициент прямой)
- угловой коэффициент прямой)
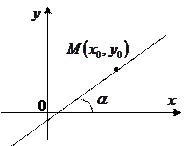
4) 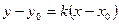 - уравнение пучка прямых (
- уравнение пучка прямых (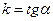 );
);
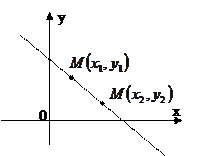
5)  - уравнение прямой, проходящей через 2 точки с коoрдинатами
- уравнение прямой, проходящей через 2 точки с коoрдинатами 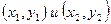 ;
;

6) 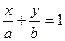 - уравнение прямой в отрезках на осях
- уравнение прямой в отрезках на осях  ;
;
3.5. Задачи на прямую на плоскости:
1)  - угол между прямыми
- угол между прямыми  и
и 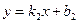 .
.
2) Условие параллельности прямых:
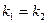 - для прямых
- для прямых  и
и 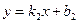 ,
,
 - для прямых
- для прямых  и
и 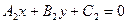 .
.
3) Условие перпендикулярности прямых:
 - для прямых
- для прямых  и
и 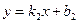 ,
,
 - для прямых
- для прямых  и
и 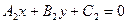 .
.
4)  - расстояние от
- расстояние от 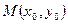 до прямой
до прямой  .
.
5) Координаты точки пересечения прямых 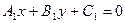 и
и 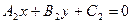 :
: 
3.6. Уравнения окружности:
 - общее уравнение кривой второго порядка.
- общее уравнение кривой второго порядка.
Определение: окружностью называется ГМТ (геометрическое место точек) плоскости, равноудаленных от одной и той же точки, называемой центром, на одно и то же расстояние, называемое радиусом.

 - уравнение окружности с центром в точке
- уравнение окружности с центром в точке 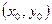 и радиусом R.
и радиусом R.
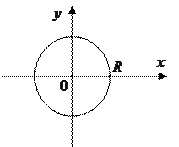
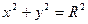 - каноническое уравнение окружности с центром в точке
- каноническое уравнение окружности с центром в точке  и радиусом
и радиусом  ;
;
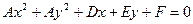 - общее уравнение окружности, т.к. коэффициенты при квадратах переменных равны и нет слагаемого, содержащего произведение переменных.
- общее уравнение окружности, т.к. коэффициенты при квадратах переменных равны и нет слагаемого, содержащего произведение переменных.
3.7. Эллипс:
Определение: эллипсом называется геометрическое место точек (ГМТ) плоскости, сумма расстояний от каждой из которых до двух данных точек, называемых фокусами, есть величина постоянная и равная 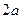 .
.
Каноническое уравнение эллипса - 
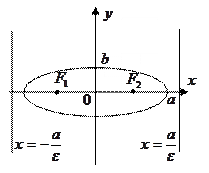 | |||||||
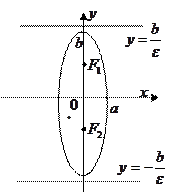 | |||||||
 | |||||||
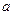 - большая полуось,
- большая полуось, 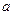 - меньшая полуось,
- меньшая полуось,
 - меньшая полуось,
- меньшая полуось,  - большая полуось,
- большая полуось,
 - полуфокусное расстояние
- полуфокусное расстояние  - полуфокусное расстояние.
- полуфокусное расстояние.



3.8. Парабола:
Определение: параболой называется ГМТ плоскости, равноудаленных от данной точки, называемой фокусом, и данной прямой, называемой директрисой.

 -каноническое уравнение параболы,
-каноническое уравнение параболы,
ветви вдоль OX, 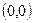 - вершина;
- вершина;
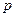 – расстояние между F и директрисой,
– расстояние между F и директрисой,
характеризует ширину раствора ее ветвей,

 - ветви вдоль OX,
- ветви вдоль OX, 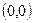 - вершина
- вершина

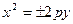 - ветви вдоль OY,
- ветви вдоль OY, 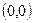 - вершина
- вершина

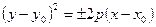 - ветви вдоль OX,
- ветви вдоль OX, 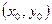 - вершина
- вершина

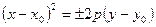 - ветви вдоль OY,
- ветви вдоль OY, 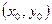 - вершина
- вершина
3.9. Гипербола:
Определение: гиперболой называется ГМТ плоскости, разность расстояний от каждой из которых до двух данных точек, называемых фокусами, есть величина постоянная и равная 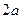 .
.
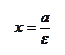   | |||
 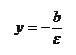 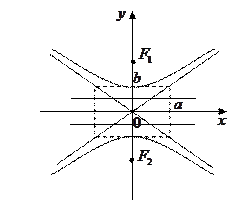 |

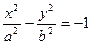
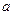 - действительная полуось
- действительная полуось 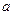 - мнимая полуось
- мнимая полуось
 - мнимая полуось
- мнимая полуось  - действительная полуось
- действительная полуось
 - полуфокусное расстояние
- полуфокусное расстояние  - полуфокусное расстояние
- полуфокусное расстояние
 - формула связи
- формула связи  - формула связи
- формула связи


 - директрисы
- директрисы  - директрисы
- директрисы
 - фокусы
- фокусы 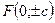
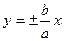 - асимптоты
- асимптоты
3.10. Плоскость в пространстве:

1)  - общее уравнение плоскости с нормальным вектором плоскости
- общее уравнение плоскости с нормальным вектором плоскости 
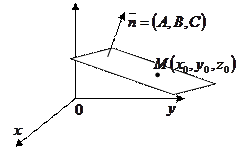 2)
2)  -
-
уравнение плоскости проходящей через 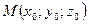 и имеющей нормальный вектор
и имеющей нормальный вектор  .
.
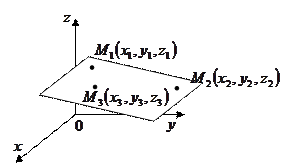 3)
3)  - уравнение плоскости, проходящей через точки
- уравнение плоскости, проходящей через точки 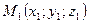 ;
;
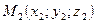 ;
; 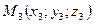 .
.

4) 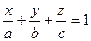 - уравнение плоскости в отрезках, где
- уравнение плоскости в отрезках, где  - отрезки, отсекаемых плоскостью на осях
- отрезки, отсекаемых плоскостью на осях  соответственно.
соответственно.
3. 11. Задачи на плоскость в пространстве:
Если  с нормальным вектором
с нормальным вектором 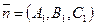
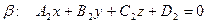 с нормальным вектором
с нормальным вектором 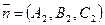 , то
, то 
1) 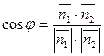 - угол между плоскостями;
- угол между плоскостями;
2)  ║
║ 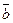

 ║
║ 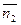 и
и 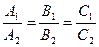 ;
;
3) 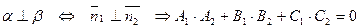 ;
;
4) Если  , то расстояние от
, то расстояние от 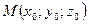 до плоскости
до плоскости  определяется формулой:
определяется формулой: 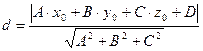 .
.
3.12. Прямая в пространстве:
 1)
1)  -канонические уравнения прямой, проходящей через
-канонические уравнения прямой, проходящей через 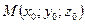 с направляющим вектором
с направляющим вектором 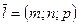 (лежащим на прямой или параллельным ей);
(лежащим на прямой или параллельным ей);
2)  - параметрические уравнения прямой;
- параметрические уравнения прямой;

3) 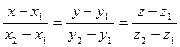 - уравнения прямой, проходящей через точки
- уравнения прямой, проходящей через точки  и
и  ;
;
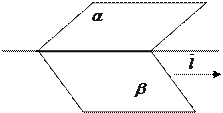
4) 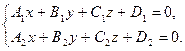 - общие уравнения прямой (линия пересечения двух не параллельных плоскостей)
- общие уравнения прямой (линия пересечения двух не параллельных плоскостей)
Направляющий вектор этой прямой:  .
.
Если подставить 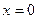 (или
(или 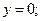 или
или 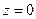 ) и решить получившуюся систему, то получим одну из точек прямой.
) и решить получившуюся систему, то получим одну из точек прямой.
3.13. Задачи на прямую в пространстве:
Если 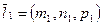 - направляющий вектор прямой
- направляющий вектор прямой 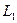 ,
,
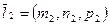 - направляющий вектор прямой
- направляющий вектор прямой  , то
, то
1) 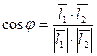 - угол между
- угол между 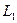 и
и  ;
;
2) 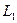 ║
║ 

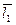 ║
║  и
и  ;
;
3) 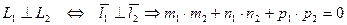 .
.
3.14. Задачи на прямую и плоскость в пространстве:
 Если
Если  с нормальным вектором
с нормальным вектором 
 :
:  - с направляющим вектором
- с направляющим вектором 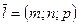 , то
, то
1) 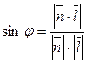 - угол между прямой и плоскостью (
- угол между прямой и плоскостью ( -величина наименьшего угла между прямой и ее проекцией на плоскость
-величина наименьшего угла между прямой и ее проекцией на плоскость  )
)
2) 

 ║
║ 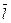 и
и 
3)  ║
║ 

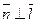 и
и 
4) Чтобы найти точку пересечения прямой и плоскости: необходимо задать прямую параметрически, подставить  в общее уравнение плоскости, решить получившееся уравнение относительно
в общее уравнение плоскости, решить получившееся уравнение относительно  и подставим
и подставим  в параметрические уравнения прямой.
в параметрические уравнения прямой.
3.15. Цилиндрические поверхности:
Определение: цилиндрической поверхностью называется поверхность, образованная движением некоторой прямой, называемой образующей, если образующая перемещается в пространстве параллельно самой себе и пересекает при этом некоторую неподвижную линию, называемую направляющей (например, 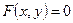 ).
).
 Если в координатном пространстве
Если в координатном пространстве  уравнение не содержит одной переменной, то оно определяет цилиндрическую поверхность, образующая которой параллельна оси отсутствующей переменной, а направляющая лежит в плоскости присутствующих переменных и задается в этой плоскости тем же уравнением, что и сама цилиндрическая
уравнение не содержит одной переменной, то оно определяет цилиндрическую поверхность, образующая которой параллельна оси отсутствующей переменной, а направляющая лежит в плоскости присутствующих переменных и задается в этой плоскости тем же уравнением, что и сама цилиндрическая
поверхность.
Например:
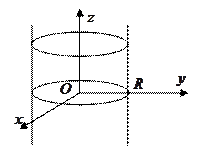
 - круговой цилиндр.
- круговой цилиндр.

 - круговой цилиндр
- круговой цилиндр

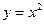 - параболический цилиндр
- параболический цилиндр

 - гиперболический цилиндр
- гиперболический цилиндр
РАЗДЕЛ IV. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА

1. 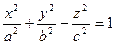 - однополостный гиперболоид (если
- однополостный гиперболоид (если
|
|
|
|
|
Дата добавления: 2015-06-28; Просмотров: 554; Нарушение авторских прав?; Мы поможем в написании вашей работы!