Лекция №2

Построение точек эллипса

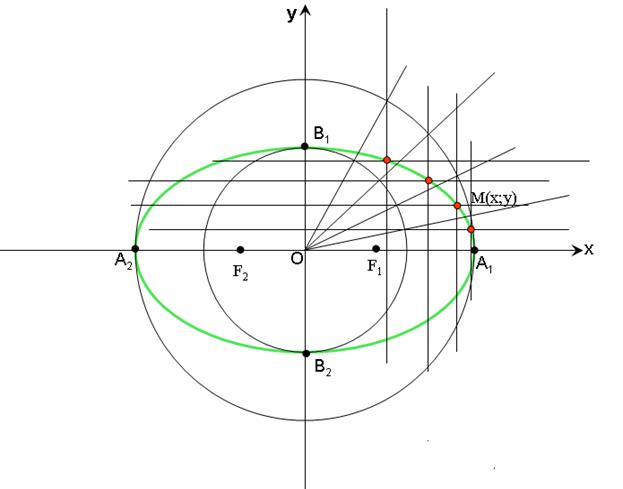
Рис.5.

Построить эллипс с полуосями и можно на основании параметрических уравнений эллипса. Этапы построения следующие:

а) Строим две соосные окружности с радиусами и .

б) Проводим произвольный луч с началом в центре окружностей.

в) Точки эллипса М получаем как точки пересечения прямой параллельной оси (Ох) и проходящей через точку пересечения луча с окружностью радиуса с прямой, параллельной оси (Оу) и проходящей через точку пересечения луча с окружностью радиуса . (См. Рис.5).

§2 Гипербола

1. Определение гиперболы и её уравнение

Определение. Гиперболой называется множество всех точек плоскости, для каждой из которых абсолютная величина разности расстояний до двух фиксированных точек плоскости F₁ и F₂ есть величина постоянная, равная 2a < ǀF₁F₂ǀ=2c.

Точки F₁ и F₂ называются фокусами гиперболы, а │ F₁F₂│= 2с ─ фокальным расстоянием.

Пусть на плоскости даны две точки F₁ и F₂. Для того чтобы составить уравнение гиперболы на плоскости введём ортонормированную систему координат, начало которой поместим с середину отрезка [F₁F₂].

Рис.6.

Ось Ох расположим таким образом чтобы точки F₁ и F₂ принадлежали этой оси. (Рис.6)

В этом случае фокусы гиперболы принимают следующие координаты F₁(c;0) и F₂(-c;0). Пусть М(х;у) ─ произвольная точка эллипса. Тогда по определению││МF₁│- │МF₂││ = 2a. (1)

По формуле вычисления расстояния между точками имеем: ; 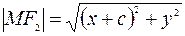. Таким образом из (1) =>

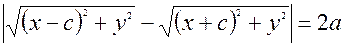. Запишем полученное выражение в виде 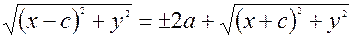и возведём в квадрат. В результате, после приведения подобных получаем . Для того чтобы освободиться от корня возведём последнее выражение в квадрат. В результате после элементарных преобразований имеем: 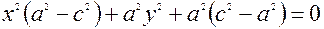. (2)

Учитывая, что 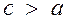и 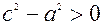, обозначим

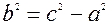
и запишем (2) виде: 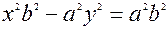. После деления полученного уравнения на получаем, что если точка М(х;у) принадлежит гиперболе, то её координаты удовлетворяют уравнению

(4)

Покажем теперь, что если координаты некоторой точки М₁(х₁;у₁) удовлетворяют уравнению (4), то точка М₁ принадлежит гиперболе.

Пусть для точки М₁(х₁;у₁) справедливо равенство (5)

Из (5) следует: (6)

Вычислим

=> .

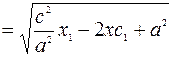
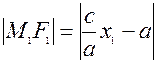Аналогично, если провести подобные преобразования для , получим .

Заметим, что из (6) следует, что .

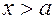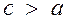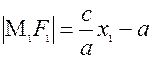Рассмотрим случай, когда x > 0. В этом случае и, так как ,то и . => 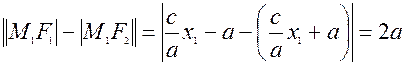, то есть точка М₁ принадлежит гиперболе.

Пусть теперь х < 0. В этом случае 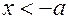, откуда следует, что и 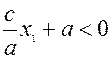. Таким образом, и . В результате получаем, что точка М₁ принадлежит гиперболе, так как .

Таким образом, уравнение (6) является уравнением гиперболы, которое называется каноническим уравнением гиперболы.

[MF₁] ─ называется первым фокальным радиусом гиперболы; 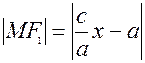. [MF₂] ─ называется вторым фокальным радиусом гиперболы; .

Заметим, => 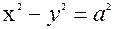такая гипербола называется равнобочной.

2. Исследование формы гиперболы по её уравнению

Пусть дан гипербола своим каноническим уравнением (6) .

Для определения вида кривой заданной уравнением (4), заметим:

а) Координаты начала системы координат точки О(0;0) не удовлетворяют

уравнению (6). => Гипербола не проходит через начало координат.

б) Найдём точки пересечения гиперболы с осью Ох: 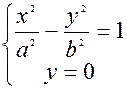=> => Эллипс две точки пересечения с осью Ох: и .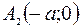

в) Найдём точки пересечения гиперболы с осью Оу: 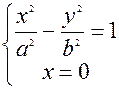=> => 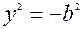Гипербола не имеет точек пересечения с осью Оу..

г) Если точка М(х;у) принадлежит гиперболе, то из уравнения (4) следует, что и точка М₁(-х;у) принадлежит гиперболе. => Гипербола симметрична относительно оси Ох.

д) Если точка М(х;у) принадлежит гиперболе, то из уравнения (4) следует, что и точка М₂(х;-у) принадлежит гиперболе. => Гипербола симметрична относительно оси Оу. На основании г) и д) можно сделать вывод, что гипербола симметрична относительно начала системы координат.

е) Из уравнения (6) , => => Все точки гиперболы лежат вне полосы, ограниченной прямыми .

ж) Выясним вопрос о взаимном расположении гиперболы с прямой 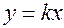, проходящей через начало координат. Для этой цели необходимо исследовать вопрос о существовании решений системы .

Подставив 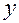из уравнения прямой в уравнение гиперболы, получаем:

. (7)

Действительные решения этого уравнения возможны в трёх случаях:

1) 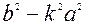> 0. Уравнение имеет два действительных решения:

, .

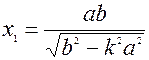В этом случае прямая 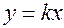пересекает гиперболу в двух, симметричных относительно начала координат, точках:

, .

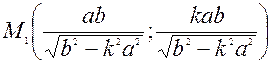2) 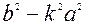≤ 0. В этом случае уравнение (7) не имеет действительных решений. Геометрически это означат, что прямые 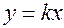не пересекаются с гиперболой.

Полученные результаты показывают, что если построить прямоугольник М₁М₂М₃М₄ сторонами и , так, чтобы стороны его были параллельны осям координат, а центр симметрии совпадает с началом системы координат, то прямые, проходящие через начало координат и расположенные внутри вертикальных углов М₁ОМ₂ и М₃ОМ₄, пересекают гиперболу.

х

Рис.7.

Таким образом, все точки гиперболы находятся в заштрихованных на рисунке 7 областях.

Заметим, что прямые ℓ₁ и ℓ₂ имеют уравнения: .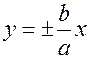

Выясним, каково поведение гиперболы по отношению к этим прямым. Так как гипербола симметричнее относительно осей координат, то достаточно рассмотреть её поведение в первой четверти.

Рис.8.

Проведём произвольную прямую ℓ перпендикулярно оси х. Пусть эта прямая имеет уравнение . Прямая ℓ пересекается с гиперболой в точке М. Для нахождения координат точки М необходимо решить систему:

.

Таким образом, точка М имеет координаты: 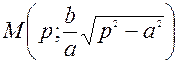. Если , то эти координаты действительны. Координаты точки L ─ точки пересечения прямой ℓ с прямой , принимают значения . Так как , то точка L лежит выше точки М. =>

.

Опустим из точки М перпендикуляр MN на прямую m. │ MN│< │LM│

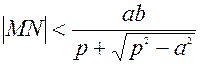=> . Выясним как ведёт себя│ MN│ при неограниченном росте параметра .

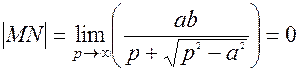=> Точки гиперболы по мере удаления от оси Оу неограниченно приближаются к прямым , но не пересекают их. Прямые называются асимптотами гиперболы.

з) Так как , то можно сделать вывод, что с ростом х величина у возрастает от 0 до ∞.

Учитывая симметричность гиперболы относительно осей координат, получаем изображение гиперболы (Рис.9).

Рис. 9.

Точки А₁, А₂, ─ называют вершинами гиперболы. [A₁A₂] ─ действительной осью гиперболы, [B₁B₂] ─ называют мнимой осью гиперболы. Числа 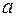и 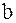называют действительной и мнимой полуосями гиперболы. (Рис.9)

Дата добавления: 2015-06-28