Решение задач

Уравнение эллипса, гиперболы и параболы в полярных координатах

Директориальное свойство эллипса и гиперболы.

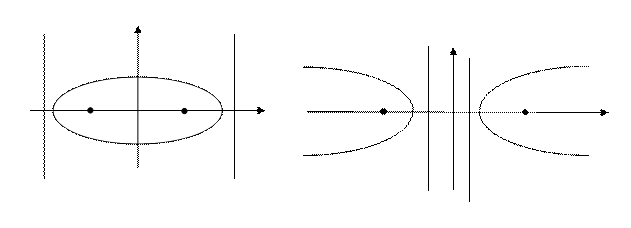
3.Фокальный параме тр.

Пусть на плоскости дан эллипс (гипербола).

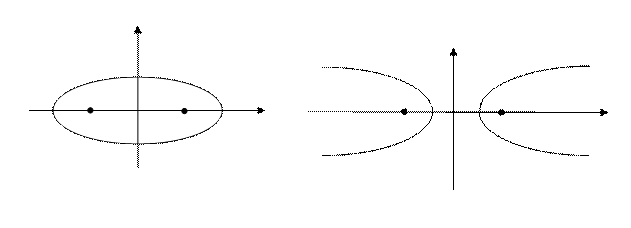
Пусть F- левый фокус эллипса, правый фокус гиперболы или просто фокус параболы. Введём полярную систему координат, начало которой поместим в точку F.

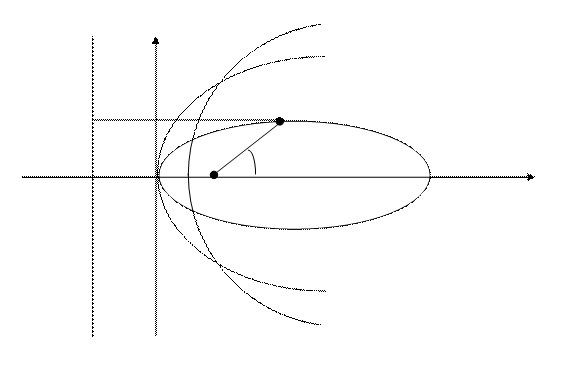
Пусть М принадлежит либо эллипсу, либо гиперболе, либо параболе, тогда 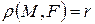. Пусть 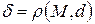. Очевидно, что .

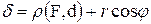Согласно директориальному свойству кривых второго порядка 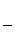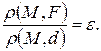=> 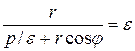. Выражая из последнего равенства 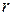, получаем:

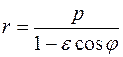
(8)

Соотношение (8) задаёт в полярной системе координат эллипс, если 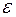˂ 1; параболу, если 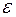= 1 и гиперболу, если 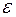> 1. Его называют полярным уравнением кривой второго порядка.

Задача №1. Составить каноническое уравнение эллипса расстояние между фокусами, которого равно 16, а большая ось ─ равна 20.

Решение.

Если расстояние между фокусами равно 16, то 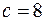и так как большая ось равна 20, то 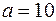. Для того чтобы составить уравнение эллипса необходимо определить значение его малой полуоси 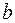. Воспользуемся следующим соотношением 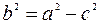=> = 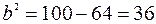> b = 6.

Следовательно, уравнение эллипса имеет вид .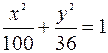

Задача №2. Составить уравнение эллипса, если эксцентриситет равен ¾ и эллипс проходит через точку А(1;1).

Решение.

Для записи канонического уравнения эллипса необходимо знать значения его большой 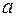и малой 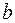полуосей.

Так как 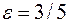, то .

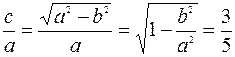
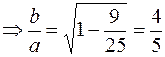С другой стороны точка А(1;1) принадлежит эллипсу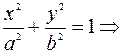

. => .

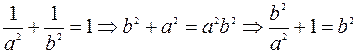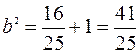Так как 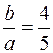, то .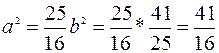

Запишем каноническое уравнение эллипса .

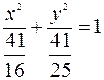Задача №3. Найти длину перпендикуляра, восстановленного из фокуса эллипса 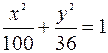к большой оси до пересечения с эллипсом.

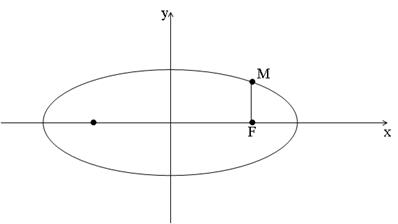Решение.

Восстановим из фокуса F

перпендикуляр до

пересечения с эллипсом

в точке М. По условию

задачи необходимо найти

длину [FM]. Координаты фокуса F(с;0) определяются по формуле 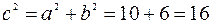. => Прямая (FM) имеет уравнение: х = 4.

Для нахождения координат точки М необходимо решить систему уравнений

=>

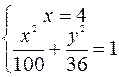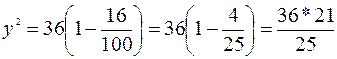
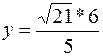=> . Очевидно, что │FM│= .

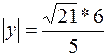Задача №4. Составить каноническое уравнение гиперболы, если её действительная ось равна 2 и расстояние между фокусами равно .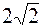

Решение.

Уравнение гиперболы имеет вид 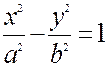. По условию задачи дано 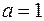и 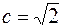. Известно, что .

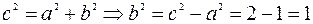Таким образом, уравнение гиперболы имеет вид .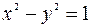

Задача №5. Составить каноническое уравнение гиперболы, если её эксцентриситет равен 13/5 и гипербола проходит через точку .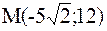

Решение.

Для составления канонического уравнения гиперболы необходимо знать значения её действительной 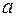и мнимо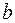й осей.

По условию задачи дано значение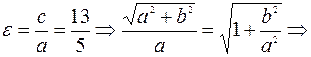

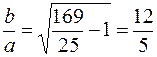. С другой стороны так как точка М принадлежит гиперболе, то её координаты удовлетворяют уравнению: 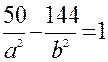. Таким образом для нахождения значений параметров 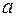и 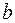, неох одимо решить систему уравнений => .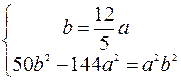

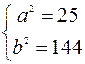Уравнение гиперболы имеет вид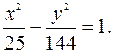

Задача №6. Составить каноническое уравнение эллипса, если его фокусы совпадают с вершинами гиперболы 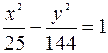, а вершины совпадают с фокусами этой гиперболы.

Решение.

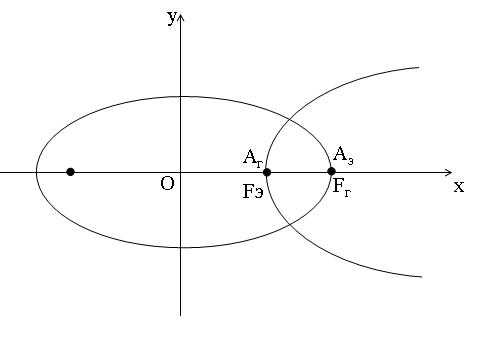
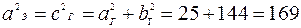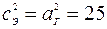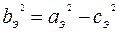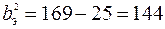Так как вершины эллипса совпадают с фокусами гиперболы, то . С другой стороны фокусы эллипса совпадают с вершинами гиперболы => . Так как для эллипса , то . Таким образом уравнение эллипса имеет вид .

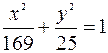Задача №7. На параболе 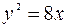найти точку, расстояние от которой до директрисы равно 4.

Решение.

Каноническое уравнение параболы имеет вид 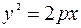, где р ─

параметр. Уравнение директрисы в общем случае записывается следующим образом 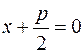. По условию задачи р = 4 и, следовательно уравнение директрисы х + 2 = 0. Если точка М принадлежит параболе, ео она имеет следующие координаты М(х; 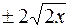). Так как расстояние от точки М до директрисы равно 4, то по формуле расстояния от точки до прямой для определения значения х, получаем уравнение: 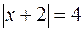. Из уравнения параболы следует, что х > 0, поэтому 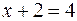=> х = 2 => М(2; ).

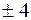Задача №8. Составить уравнение параболы с вершиной в начале координат, симметричной относительно оси (Оу) и отсекающей на прямой у = х хорду длины .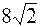

Решение.

Пусть парабола имеет уравнение 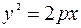. С прямой у = х она имеет две точки пересечения: М₁(0;0) и М₂(х; 2рх). Длина хорды, очевидно равна

│М₁М₂│= │2рх│ = 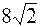. Так как р > 0, то 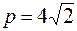. Искомое уравнение параболы имеет вид .

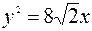Задача №9. Парабол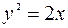а отсекает от прямой, проходящей через начало координат, хорду длина которой равна 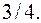Написать уравнение этой прямой.

Решение.

Пусть парабола имеет уравнение 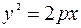. С прямой 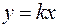она имеет две точки пересечения: М₁(0;0) и 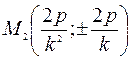. Длина хорды, очевидно равна 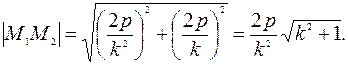Так как, по условию задачи р = 1 и длина хорды равна 3/4, то для определения параметра 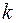получаем уравнение => => => =>

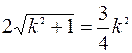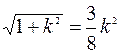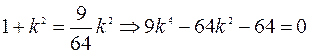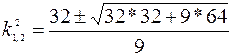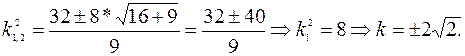=> Таким образом существуют две прямые 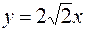и 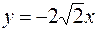, от которых парабола 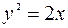отсекает хорду длиной 3/4.

Задача №10. На параболе 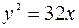найти точку, расстояние от которой до прямой 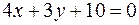равно 2.

Решение.

Если точка М(х;у) лежит на параболе 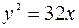, то она имеет координаты .

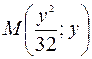Из формулы расстояния от точки до прямой на плоскости следует 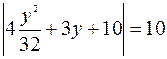. => а) 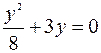=> 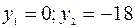. Таким образом точки М₁(0;0) и М₂(18;-24) параболы удалены от прямой 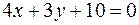на расстояние, равное 2.

б) 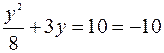─ это уравнение не имеет действительных корней.

Литература

1. Атанасян Л.С, Базырев В.Т. Геометрия. В 2-х частях. Ч 1 Учебное пособие для студентов физико-математических факультетов пединститутов – М.: Просвещение, 1986.-336 с.

2. Атанасян Л.С., Цаленко М.М. Задачник практикум по геометрии. М.: Просвещение, 1994. – 192 с.

3. Базылев В.Т. и др. Геометрия. Учебное пособие для студентов 1 курса физико-математических факультетов пединститутов М.: Просвещение, 1974.

4. Сборник задач по геометрии/ С.А. Франгулов, П.Н. Совертков, А.А. Фадеева, Т.П. Ходот – М.: Просвещение, 2002 – 238 с.

Дата добавления: 2015-06-28