КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Гипербола. Кривые второго порядка
|
|
|
|
Эллипс
Окружность
Кривые второго порядка.
Окружностью называется множество точек плоскости, равноудалённых от данной точки (це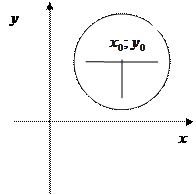 
нтра). Уравнение окружности: 
, где (
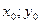) - координаты центра окружности. Общее уравнение окружности 
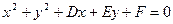. Если центр находится в начале координат, то получится каноническое уравнение окружности: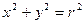 
Эллипсом называетсямножествоточек плоскости, сумма расстояний до двух данных точек, называемых фокусами, есть постоянная величина, равная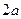 
.
Каноническое уравнение эллипса: 
, где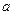 
- длина большой полуоси,
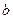- длина малой полуоси, 
.
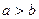Расстояние между фокусами -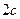 
.
Параметры эллипса связаны следующими
соотношениями: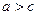 
; 
.
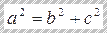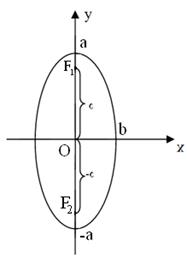
Если 
, то фокусы находятся на оси ОХ,
если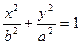 
, то фокусы находятся на оси OY.
Эксцентриситет эллипса -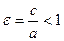 
.
Фокальные радиусы – это расстояния от точки М(х;у) эллипса до его фокусов: 
Гиперболой называется геометрическое место точек, разность расстояний от которых до двух данных точек, называемых фокусами, есть постоянная величина, равная 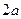. Каноническое уравнение гиперболы: 
, где 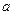- длина вещественной полуоси, 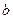- длина мнимой полуоси. Расстояние между фокусами - . 
; 
.
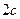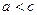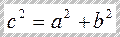Если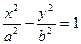 
, то фокусы находятся на оси OX, если 
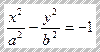, то фокусы находятся на оси OY.
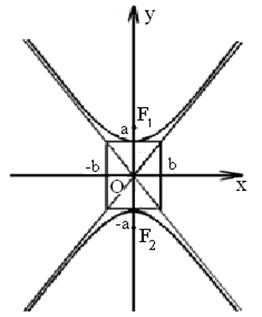Эксцентриситет гиперболы 
.
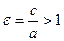Фокальные радиусы – это расстояния от точки М(х;у) гиперболы до его фокусов: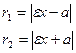 
.
Прямые, заданные уравнениями 
являются асимптотами гиперболы. Если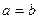 
, то гипербола равносторонняя 
|
|
|
|
|
Дата добавления: 2015-06-28; Просмотров: 852; Нарушение авторских прав?; Мы поможем в написании вашей работы!