Определение внутренних сил, напряжений и деформаций при сдвиге

Сдвигом называется такой вид нагружения бруса, при котором в его поперечных сечениях из шести составляющих главного вектора и главного момента внутренних сил, от нуля отличается только поперечная сила. Данный вид нагружения встречается редко и чаще всего он сопровождается изгибающими моментами. Однако, в некоторых случаях, например, в заклепочных и сварных соединениях при раскройных работах имеет место близкое к сдвигу нагружение бруса (рис. 5.2).

Внутренняя поперечная сила Q в поперечном сечении бруса на участке действия сосредоточенных сил определяется методом сечений и равна Р. Если расстояние между сосредоточенными силами (например, расстояние между ножами при раскрое материала) мало, то можно пренебречь величиной изгибающего момента. При этом распределение касательных напряжений по сечению неравномерно, так как внешняя поверхность бруса свободна от осевой нагрузки и по закону парности касательных напряжений, в верхних и нижних точках сечения касательные напряжения равны нулю (рис. 5.3).

Как показывают исследования, распределение касательных напряжений весьма близко к равномерному закону (рис. 5.3) и поэтому в первом приближении для упрощения расчетов заменяется равномерным законом распределения. Тогда

.

Таким образом, касательное напряжение при сдвиге (срезе) определяется уравнением:

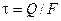, (5.8)

где F - площадь среза.

Деформация бруса при сдвиге в зоне действия усилия, предшествующая разрушению от среза, заключается в перекашивании прямых углов элемента (рис. 5.4).

Аналогично растяжению (сжатию) закон Гука при сдвиге в абсолютных координатах имеет вид:

. (5.9)

где G - модуль сдвига или модуль упругости второго рода.

Модуль сдвига связан с модулем упругости первого рода и коэффициентом Пуассона следующим, что подтверждают опыты, уравнением:

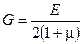. (5.10)

Для стали модуль сдвига примерно равен 8×10⁴ МПа. Из уравнения (5.9) с учетом (5.8) может быть получен закон Гука при сдвиге в относительных координатах:

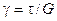, (5.11)

или

. (5.12)

Закон Гука справедлив лишь до предела пропорциональности. При испытаниях на сдвиг образцов из пластичных материалов так же, как и при растяжении, имеет место явление текучести. Предел текучести обозначается t_т, а предел прочности - t _в.

Дата добавления: 2015-06-28