Залежність моментів інерції щодо двох рівнобіжних осей, одна з яких центральна

Центральні осі X,Y, щодо яких відцентровий момент інерції Ixy дорівнює нулю, називаються головними осями інерції, а осьові моменти інерції Ix і Iy щодо цих осей називаються головними моментами інерції.

Рис.5.3.

Приклад 3. Визначення осьових моментів інерції для прямокутника.

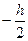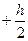Осьовий момент інерції щодо центральної осі Х дорівнює . Візьмемо на відстані y елементарну площадку dА – смужку шириною dy. Площа , підставимо під інтеграл та проінтегруємо від до . Одержимо: .

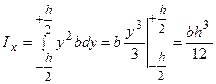Рис.5.4.

Міркуючи аналогічно, визначимо осьовий момент інерції щодо осі Y, тобто:

.

Приклад 4. Визначення моментів інерції для круглого перерізу (рис.5.5а).

Визначимо полярний момент інерції . На відстані r виділимо елементарну площадку dА – кільце шириною dr. Очевидно, що 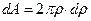. Підставимо значення dА в інтеграл та інтегруємо від 0 до . Одержимо: . Але полярний момент інерції дорівнює сумі осьових моментів інерції, тобто 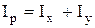. Очевидно, що для круглого перерізу I_x = I_y. Тоді I_p = 2I_x і 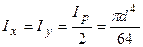. На підставі отриманих формул легко одержати значення моментів інерції для кільцевого перерізу (рис.5.5б). Осьовий момент інерції щодо центральних осей складеного перерізу дорівнює сумі осьових моментів інерції щодо цих осей складених площ, тобто осьовий момент інерції кільцевого перерізу:

,

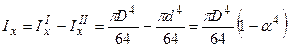тут 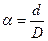. Очевидно і для кільцевого перерізу I_x = I_y. Аналогічно визначимо полярний момент інерції: .

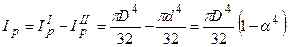Рис.5.5.

Дано: переріз площею A; відоме положення центральних осей X,Y; відомі осьові I_x і I_y та відцентровий моменти інерції I_xy. Визначити моменти інерції I_x1, I_y1, I_x1y1 щодо осей X₁ і Y₁, рівнобіжних центральним осям, якщо відомі відстані a і b між осями.

Виділимо елементарну площадку dА та визначимо її координати в системі координат X₁Y₁: 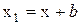; . Осьовий момент інерції щодо осі X₁ запишеться як: 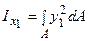. Підставимо значення х₁ і y₁ та інтегруємо, одержимо: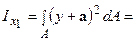 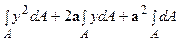. Перший інтеграл являє собою осьовий момент інерції щодо центральної осі X: 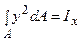; другий – статичний момент площі щодо центральної осі тотожно дорівнює нулю: ; третій – площа перерізу. Таким чином: . Аналогічно визначимо осьовий момент інерції щодо осі Y₁:

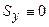, (, тому що вісь Y – центральна). Таким чином, осьовий момент інерції щодо осі, рівнобіжної центральній осі, дорівнює осьовому моменту інерції щодо центральної осі плюс добуток площі на квадрат відстані між осями.

Рис.5.6. Рис.5.7.

Аналогічно визначимо відцентровий момент інерції:

.

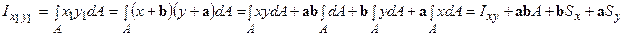З обліком того, що S_x і S_y º 0, маємо 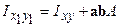. Відцентровий момент інерції щодо осей, рівнобіжних центральним осям, дорівнює відцентровому моменту інерції щодо центральних осей плюс добуток площі на відстані між осями, які потрібно брати з відповідними знаками.

Моменти опору. Розглянемо переріз площею A. Х,Y – головні осі перерізу, I_x, I_y – головні осьові моменти інерції. Відношення осьового моменту інерції щодо осі до відстані до найбільш віддаленої точки перерізу від цієї осі називається осьовим моментом опору, тобто 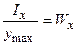, [м³].

Практичне значення мають моменти опору щодо головних центральних осей для симетричних фігур, що звичайно називають просто моментами опору.

1. Для прямокутника (рис.5.4): 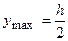, , 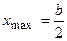, , 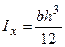тоді , .

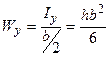2. Для круглого перерізу (рис.5.5а): 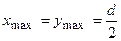, , тоді .

3. Для кільцевого перерізу (рис.5.5б): , , тоді

.

Полярним моментом опору називається відношення полярного моменту інерції до відстані від полюса до найбільш віддаленої точки: 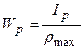,[см³, м³]. Для круглого перерізу: , , 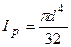тоді . Для кільцевого перерізу: , , 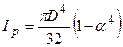тоді .

Дата добавления: 2015-06-28