Лекція 6.Згинання прямолінійних стержнів

Згинанням називається тип деформування стержня, при якому в його поперечних перерізах виникають згинальні моменти.

Класифікація згинання. Згинання підрозділяється на поперечне – зовнішнє навантаження діє в напрямку, перпендикулярному осі стержня, подовжнє - зовнішні сили діють уздовж осі стержня та подовжньо -поперечне.

Поперечне згинання підрозділяється на плоске, при якому згинальні сили лежать в одній площині, та просторове, при якому зовнішні згинальні сили довільно орієнтовані у просторі.

Плоске згинання підрозділяється на пряме та косе. У випадку прямого згинання площина дії згинальних навантажень збігається з однією з головних осей інерції перерізу. На рис 6.1 показаний випадок навантаження стержня при прямому поперечному згинанні. Зовнішні сили розташовані у площині УОZ, що збігається з головною віссю перерізу Y. При косому згинанні площина дії згинальних навантажень не збігається з жодною з головних осей інерції.

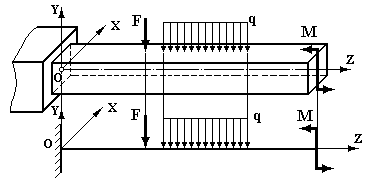
Рис.6.1.

З прямого поперечного згинання (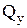 ¹ 0 і 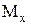¹ 0) виділяється чисте згинання, при якому поперечна сила 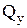дорівнює нулю, а згинальний момент 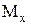є єдиним внутрішнім силовим фактором у перерізу стержня і виявляється постійним на ділянці стержня.

Розглянемо згинання балок. Балкою називається стержень, закріплений на опорах та працюючий на згинання. Кількість зовнішніх зв'язків в опорах забороняє переміщення балки як твердого цілого. Плоскі опори балок та реактивні зусилля в них показані на рис.6.2.

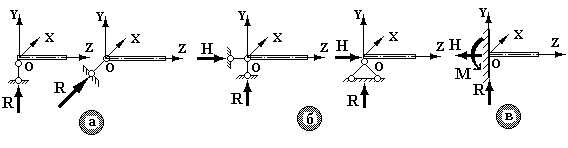
Рис.6.2.

У шарнірно-рухомій опорі (рис.6.2а) виникає одна реактивна сила R, що діє перпендикулярно поверхні опори (у напрямку показаного зв'язку). У шарнірно-нерухомій опорі (рис.6.2б) виникають дві складових реакції: вертикальна R і горизонтальна H. У затисненні (жорсткому затисненні) (рис.6.2в), виникають три складових: вертикальна R, горизонтальна H і момент M.

Для кінематичної незмінюваності плоских балок необхідна кількість зовнішніх зв'язків три, причому при плоскому згинанні горизонтальна складова H реакції в шарнірно-нерухомій опорі тотожно дорівнює нулю. Тому надалі використовуємо два рівняння рівноваги. Якщо кількість зовнішніх поперечних зв'язків більше двох, то така балка називається статично невизначеною (багатоопорною). Типи і найменування балок, що зустрічаються, показані на рис.6.3.

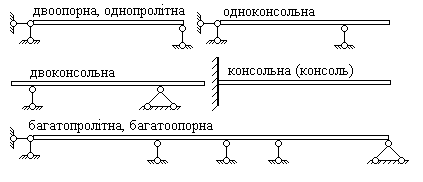
Рис. 6.3.

Поперечна сила та згинальний момент 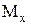. Проаналізуємо внутрішні силові фактори у поперечному перерізі балки при прямому поперечному згинанні, а потім сформулюємо основні правила побудови епюр і .

Розглянемо консольний стержень з затисненим правим торцем та навантажений силами F₁ і F₂ (рис 6.4). Нехай F₁> F₂.

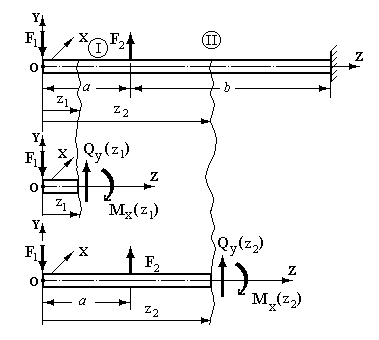
Рис.6.4.

Скористаємося методом перерізів. Виберемо переріз на першій і другій ділянках, покажемо відсічені частини, замінимо дію відкинутих частин на залишену внутрішніми силовими факторами і _.З умов статики (суми проекцій сил на вісь Y та суми моментів щодо осі X, що проходить через центр ваги розглянутого перерізу) визначимо їхні значення.

1 ділянка: SF_i = - F₁ + (z₁) = 0, відкіля (z₁) = F₁;

SM_i = F₁×z₁ – (z₁) = 0, відкіля (z₁) = F₁×z₁.

2 ділянка, SF_i = - F₁ + F₂ + (z₂) = 0, відкіля (z₂) = F₁ – F₂;

SM_i = F₁×z₂ - F₂×(z_2-а) - (z₂) = 0, відкіля (z₂)= F₁×z₂ – F₂×(z_2-а).

Використовуючи такі уявлення, сформулюємо наступні правила для визначення поперечної сили та згинального моменту при згинанні.

Поперечна сила в даному перерізі – (z) чисельно дорівнює алгебраїчній сумі проекцій на нормаль (вісь Y) до осі стержня всіх сил, розташованих по одну сторону від перерізу (всіх однобічних сил), та утворює заміну дії відкинутої частини на залишену. Правило знаків. Поперечна сила вважається позитивною (додатною), якщо обертає розглянуту відсічену частину балки щодо центра ваги перерізу за годинниковою стрілкою, та негативною (від’ємною) - якщо проти годинникової стрілки.

Згинальний момент в даному перерізі – 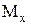(z) чисельно дорівнює алгебраїчній сумі моментів щодо центра ваги перерізу всіх сил, розташованих по одну сторону від перерізу (всіх однобічних сил), та утворює заміну дії відкинутої частини на залишену. Правило знаків. Згинальний момент вважається позитивним (додатним), якщо відсічена частина згинається опуклістю вниз (стиснуте волокно вгорі, розтягнуте внизу), та негативним (від’ємним)- якщо навпаки. Таким чином, епюра згинальних моментів будується з боку стиснутого волокна.

Схематично прийняті правила знаків виглядають так:

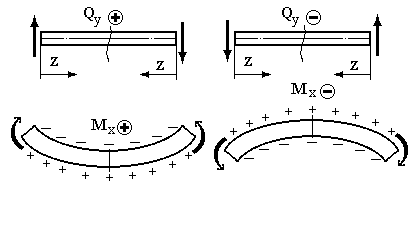
Рис. 6.5.

Диференціальні залежності між інтенсивністю зовнішнього розподіленого навантаження q поперечною силою та згинальним моментом 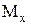. Розглянемо балку, навантажену довільним розподіленим навантаженням q(z) (рис.6.6а). В перерізі на відстані 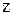виділимо елемент довжиною dz (рис. 6.6а). В перерізі I діють внутрішні силові фактори і , в перерізі II на відстані 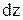від першого діють внутрішні зусилля +d і +d . У межах нескінченно малого dz навантаження q(z) можна вважати рівномірно розподіленим та рівним q.

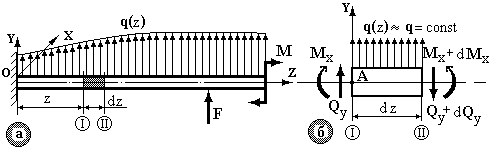
Рис. 6.6.

Так як балка під дією зовнішнього навантаження знаходиться в рівновазі, то і кожен її елемент під дією зовнішніх та внутрішніх зусиль також знаходиться в рівновазі (рис. 6.6б).

Запишемо умови статичної рівноваги:

1. 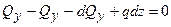, відкіля 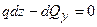, отже

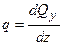. (6.1)

2. 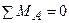; 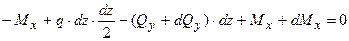, приводячи подібні члени та зневажаючи нескінченно малими другого порядку в порівнянні з нескінченно малими першого порядку, одержимо: 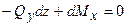, відкіля:

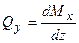. (6.2)

3. Підставляючи вираз (6.2) у залежність (6.1), одержимо:

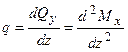. (6.3)

Диференціальні залежності (6.2) і (6.3) дозволяють установити деякі особливості розподілів поперечних сил та згинальних моментів. Приведені нижче правила можуть використовуватися для побудови та перевірки епюр і .

1. На ділянках, де розподілене навантаження відсутнє (q=0), епюра постійна, а епюра представляє лінійну функцію.

2. На ділянках з рівномірно розподіленим навантаженням 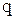епюра лінійна, а епюра 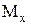- квадратна парабола, причому опуклість параболи спрямована в протилежну сторону дії розподіленого навантаження. У точці 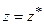, де поперечна сила 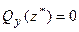(змінює знак), момент досягає екстремального значення ().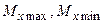

3. На ділянках, де 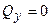, епюра 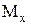постійна.

4. Наступні пункти сформульовані для правої осі z (для правої системи координат). На ділянці, де поперечна сила позитивна, епюра моменту зростає, і убуває - якщо негативна.

5. У перерізах, де до балки прикладені зовнішні зосереджені сили:

а) на епюрі 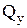спостерігаютьсястрибки на їхню величину й у напрямку прикладених зосереджених сил;

б) на епюрі з'являються злами, причому вістря зламів спрямовані проти дії зосереджених сил.

6. У перерізах, де до балки прикладені зосереджені моменти, на епюрі спостерігаються стрибки на величини цих моментів.

7. Епюра являє собою діаграму першої похідної від функції моменту , тобто ординати пропорційні тангенсу кута нахилу дотичної до епюрі .

Далі розглянемо приклади побудови епюр поперечних сил та згинальних моментів .

Дата добавления: 2015-06-28